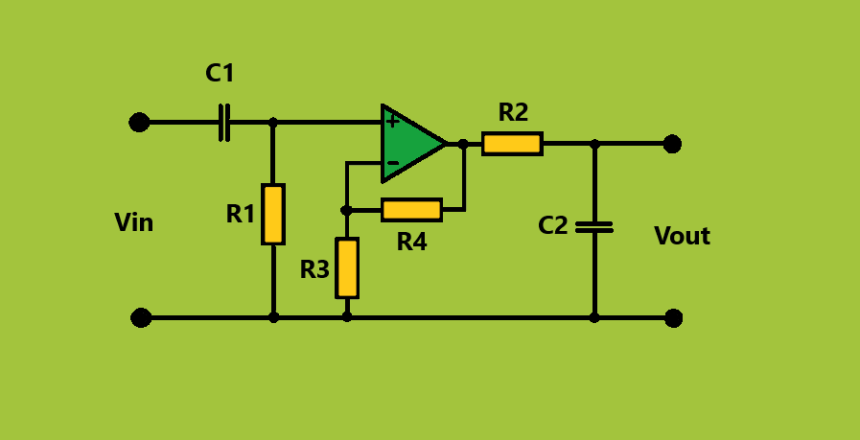
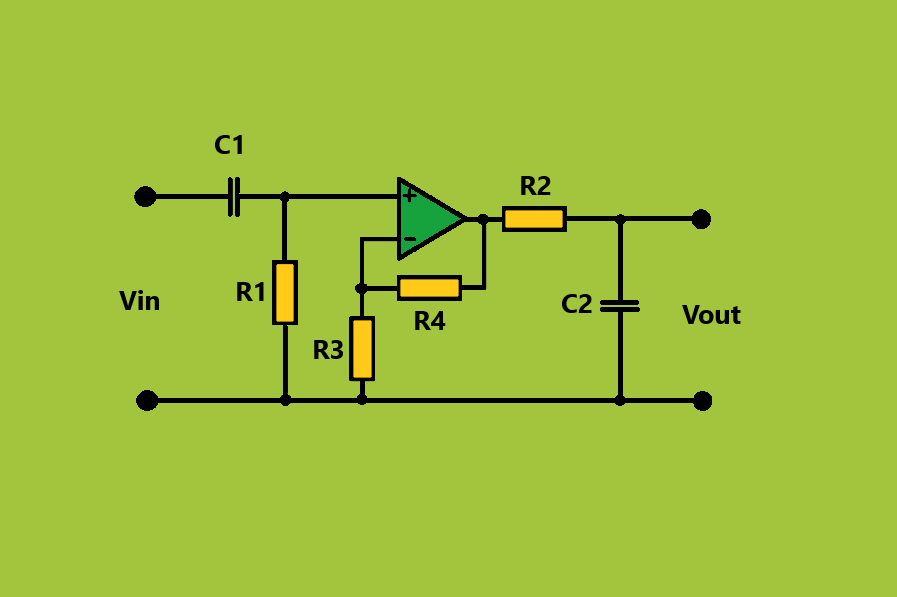
ویژگی اصلی یک فیلتر میان گذر یا هر فیلتر مشابه آن، توانایی آن در عبور فرکانسهای نسبتا تضعیفنشده از یک باند مشخص یا گسترهای از فرکانسها به نام «باند عبور» است.
برای فیلتر پایینگذر، این باند عبور از صفر هرتز یا DC شروع میشود و تا نقطه فرکانس قطع مشخص یعنی 3 دسیبل پایینتر از حداکثر گین باند عبور ادامه مییابد. به همین ترتیب، برای یک فیلتر بالاگذر، باند عبور از این فرکانس قطع منفی 3 دسیبل شروع میشود و تا بینهایت یا حداکثر گین حلقهباز برای یک فیلتر فعال ادامه مییابد.
با این حال، فیلتر میانگذر اکتیو کمی متفاوت است، زیرا یک مدار فیلتر انتخابی فرکانس است که در سیستمهای الکترونیکی برای جدا کردن سیگنال در یک فرکانس خاص، یا طیف وسیعی از سیگنالهایی که در یک «باند» فرکانسی قرار دارند، استفاده میشود. این باند یا محدوده فرکانسها بین دو نقطه فرکانس قطع یا گوشه با برچسب «فرکانس پایین» (ƒL) و «فرکانس بالا» (ƒH) قرار دارد و سیگنالهای خارج از محدوده این دو نقطه تضعیف میشوند.
فیلتر میانگذر اکتیو ساده را میتوان به راحتی با کسکود کردن یک فیلتر پایینگذر با یک فیلتر بالاگذر، همچون شکل پایین، ساخت.

فرکانس قطع یا گوشه فیلتر پایینگذر (LPF) بالاتر از فرکانس قطع فیلتر بالاگذر (HPF) است و تفاوت بین فرکانس ها در نقاط منفی 3 دسیبل، «پهنای باند» را تعیین میکند و هرگونه سیگنال خارج از محدوده این نقاط باید تضعیف شود. یکی از راههای ساخت یک فیلتر میانگذر اکتیو بسیار ساده، اتصال فیلترهای پسیو بالاگذر و پایینگذر پایه به یک مدار تقویتکننده عملیاتی به شکل زیر است که قبلا طرز کارشان را یاد گرفتهایم.
مدار فیلتر میانگذر اکتیو
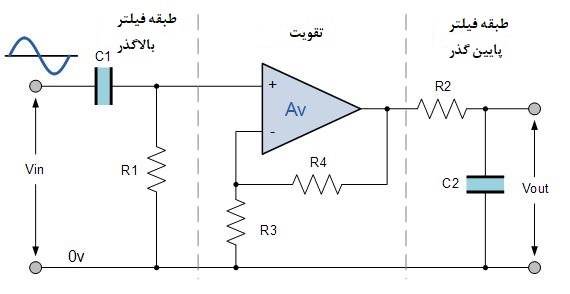
این ساختار کسکود از فیلترهای پسیو پایینگذر و بالاگذر مجزا، یک مدار فیلتر با ضریب Q پایین تولید میکند که دارای یک باند عبور وسیع است. اولین طبقه فیلتر، طبقه بالاگذر خواهد بود که از خازن برای جلوگیری هرگونه بایاس DC از منبع استفاده میکند. این طرح دارای مزیت تولید یک پاسخ فرکانسی نامتقارن نسبتا مسطح میانگذر همچون شکل زیر است که یک نیمه نشاندهنده پاسخ پایینگذر و نیمی دیگر نشاندهنده پاسخ بالاگذر میباشد.
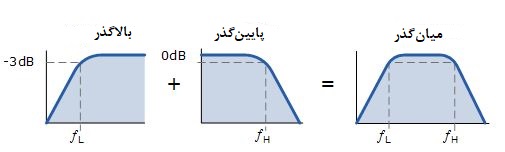
نقطه فرکانس قطع بالا ( ƒH ) و همچنین نقطه فرکانس قطع پایین ( ƒL ) مانند قبل در مدارهای فیلتر پایینگذر و بالاگذر استاندارد درجه اول محاسبه میشود. بدیهی است که برای جلوگیری از هر گونه تعامل بین طبقات پایینگذر و بالاگذر، یک ایزولاسیون منطقی بین دو نقطه قطع لازم است. تقویتکننده هم ایزولاسیون بین دو طبقه را فراهم میکند و هم گین ولتاژ کلی مدار را تعیین میکند.
بنابراین پهنای باند فیلتر، اختلاف بین این نقاط بالا و پایین منفی 3 دسیبل است. برای مثال، فرض کنید یک فیلتر میانگذر داریم که نقاط فرکانس قطع منفی 3 دسیبل آن روی 200 هرتز و 600 هرتز تنظیم شدهاست. پس پهنای باند فیلتر به صورت زیر محاسبه میشود:
Bandwidth (BW) = 600 – 200 = 400Hz
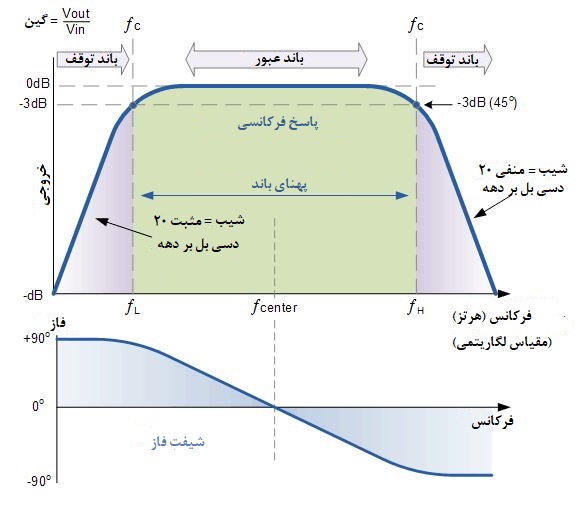
پاسخ فرکانسی و شیفت فاز نرمالیزه برای فیلتر میانگذر اکتیو به صورت زیر خواهد بود.
پاسخ فرکانسی فیلتر میانگذر اکتیو
در حالی که مدار تنظیمشده فیلتر پسیو فوق به عنوان فیلتر میانگذر کار میکند، باند عبور (پهنای باند) میتواند بسیار گسترده باشد و اگر بخواهیم باند کوچکی از فرکانسها را جدا کنیم، ممکن است مشکل ایجاد شود. فیلتر میانگذر اکتیو میتواند با استفاده از تقویتکننده عملیاتی معکوس نیز ساخته شود.
بنابراین با تنظیم مجدد موقعیتهای مقاومتها و خازنها در داخل فیلتر، میتوانیم مدار فیلتر بسیار بهتری را مطابق شکل زیر تولید کنیم. برای فیلتر میانگذر اکتیو، نقطه فرکانس قطع پایین با ƒC1 و نقطه فرکانس قطع بالا با fC2 نشان داده میشود.
مدار فیلتر میانگذر اکتیو با تقویتکننده معکوس
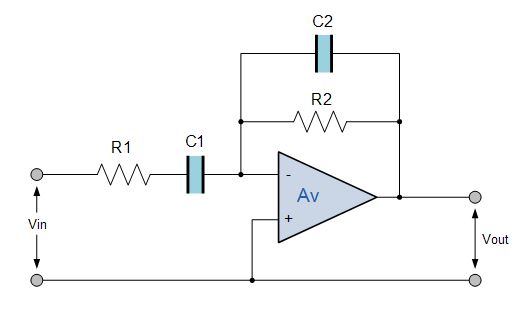
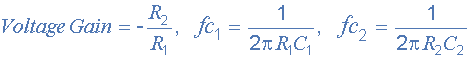
این نوع فیلتر میانگذر به گونهای طراحی شدهاست که باند عبور بسیار باریکتری داشته باشد. فرکانس مرکزی و پهنای باند فیلتر به مقادیر R1 ، R2، C1 و C2 بستگی دارد. خروجی فیلتر بازهم از خروجی آپ امپ گرفته میشود.
فیلتر میانگذر اکتیو چند فیدبکه
میتوانیم پاسخ باند عبور مدار فوق را با مرتب کردن مجدد اجزا برای تولید فیلتر میانگذر گین – بینهایت چند فیدبکه (IGMF) بهبود دهیم. این نوع طراحی فیلتر میانگذر اکتیو یک مدار «تنظیم شده» بر اساس فیلتر اکتیو فیدبک منفی ایجاد میکند که برای آن مقدار «ضریب Q» بالا (تا 25) و شیب پایینروندگی تیز در دو طرف فرکانس مرکزی فراهم میکند. از آنجایی که پاسخ فرکانسی مدار مشابه مدار تشدید است، به این فرکانس مرکزی، فرکانس تشدید (ƒr) گفته میشود. مدار زیر را در نظر بگیرید:
فیلتر اکتیو گین-بینهایت چند فیدبکه
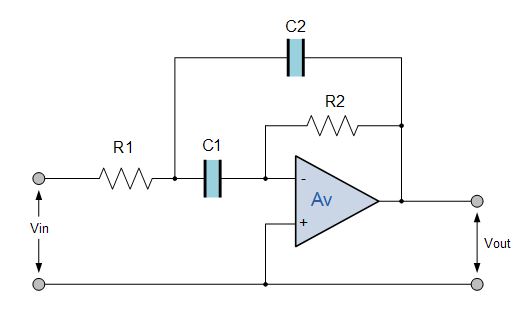
این مدار فیلتر میانگذر اکتیو از گین کامل تقویتکننده عملیاتی، با چند فیدبک منفی از طریق مقاومت R2 و خازن C2 استفاده میکند. پس میتوانیم ویژگیهای فیلتر IGMF را به صورت زیر تعریف کنیم:
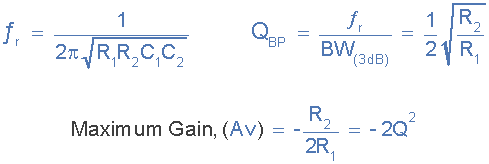
پس میتوانیم ببینیم که رابطه بین مقاومتهای R1 و R2، «ضریب Q» باند عبور را تعیین میکند و در فرکانسی که در آن حداکثر دامنه رخ میدهد، گین مدار برابر با خواهد بود. پس با افزایش گین، انتخابی بودن نیز افزایش مییابد. به عبارت دیگر، گین بالا – انتخابی بودن (Selectivity) بالا.
مثال اول فیلتر میانگذر اکتیو
یک فیلتر میانگذر اکتیو که دارای گین ولتاژ (AV) یک و فرکانس تشدید (fr) یک کیلوهرتز است با استفاده از یک مدار فیلتر میانگذر گین-بینهایت چند فیدبکه ساخته شدهاست. مقادیر المانهای مورد نیاز برای اجرای مدار را محاسبه کنید.
ابتدا میتوانیم مقادیر دو مقاومت R1 و R2 مورد نیاز فیلتر اکتیو را با استفاده از گین مدار برای یافتن Q به صورت زیر تعیین کنیم.
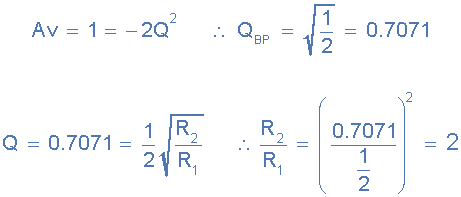
پس متوجه میشویم که مقدار Q = 0.7071 رابطهای از مقاومت را نشان میدهد که مقدار R2 دو برابر مقدار مقاومت R1 است. پس میتوانیم هر مقدار مناسبی از مقاومتها را انتخاب کنیم تا نسبت عدد 2 مورد نیاز را به دست آوریم. پس مقاومتها را اینگونه انتخاب میکنیم: R1 = 10kΩ و R2 = 20kΩ.
فرکانس مرکزی یا تشدید 1 کیلوهرتز داده شدهاست. بنابراین، با استفاده از مقادیر جدید مقاومت میتوانیم مقدار خازنهای مورد نیاز را با فرض C = C1 = C2 تعیین کنیم.
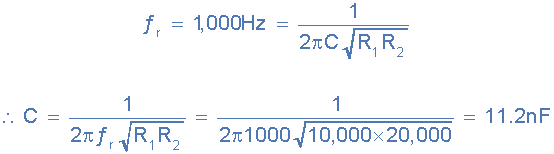
نزدیکترین مقدار استاندارد برای مقدار خازن 10 نانوفاراد است.
نقطه فرکانس تشدید
شکل واقعی منحنی پاسخ فرکانسی برای هر فیلتر میانگذر پسیو یا اکتیو به ویژگیهای مدار فیلتر بستگی دارد که منحنی فوق به عنوان یک پاسخ میانگذر «ایدهآل» تعریف شدهاست. یک فیلتر میانگذر اکتیو یک فیلتر درجه دوم است زیرا دارای «دو» جزء راکتیو (دو خازن) در طراحی مدار خود است.
در نتیجه این دو جزء راکتانسی، فیلتر یک پاسخ پیک یا فرکانس تشدید (ƒr) در «فرکانس مرکزی» خود، ƒc خواهد داشت. فرکانس مرکزی به طور کلی به عنوان میانگین هندسی دو فرکانس قطع منفی3 دسیبل بالا و پایین محاسبه میشود که فرکانس تشدید (نقطه نوسان) به صورت زیر داده میشود:
که در فرمول بالا، تعریف پارامترها به شکل زیر است:
- Fr : فرکانس مرکزی یا تشدید
- FL : فرکانس قطع منفی 3 دسیبل پایین
- FH : فرکانس قطع منفی 3 دسیبل بالا
در مثال ساده ما در بالا که فیلترها دارای فرکانس قطع منفی 3 دسیبل بالا و پایین 600 هرتز و 200 هرتز بودند، فرکانس مرکزی یا تشدید فیلتر میانگذر اکتیو به این صورت خواهد بود:
ضریب کیفیت یا Q
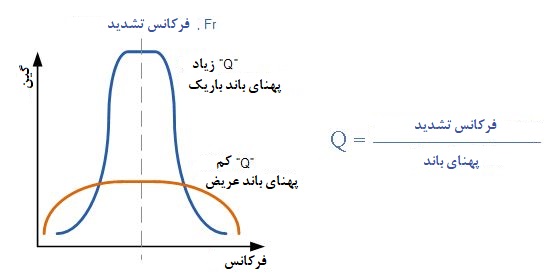
در مدار فیلتر میانگذر، عرض کلی باند عبور واقعی بین نقاط فرکانس قطع منفی 3 دسیبل بالا و پایین فیلتر، ضریب کیفیت یا نقطه Q مدار را تعیین میکند. این ضریب Q معیاری از میزان «انتخابی» یا «غیرانتخابی» فیلتر میانگذر نسبت به گسترهای معینی از فرکانسها است. هرچه مقدار ضریب Q کمتر باشد، پهنای باند فیلتر بیشتر است و هر چه ضریب Q بیشتر باشد، فیلتر باریکتر و «انتخابیتر» است.
به ضریب کیفیت یا Q فیلتر گاهی اوقات نماد یونانی آلفا، (α) داده میشود و به عنوان فرکانس اوج آلفا شناخته میشود که در آن:
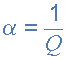
از آنجایی که ضریب کیفیت یک فیلتر میانگذر اکتیو (سیستم درجه دوم) به تیزی پاسخ فیلترها در اطراف فرکانس تشدید مرکزی آن (ƒr) مربوط میشود، میتوان آن را به عنوان «عامل میرایی» یا «ضریب میرایی» نیز در نظر گرفت زیرا هر چه فیلتر میرایی بیشتری داشته باشد، پاسخ آن صافتر است و به همین ترتیب، اگر فیلتر میرایی کمتری داشته باشد، پاسخ آن تیزتر خواهد بود. نسبت میرایی نماد یونانی (کسی یا kesi)، (ξ) است که در آن:
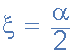
مقدار Q فیلتر میانگذر همان نسبت فرکانس تشدید (fr) بر پهنای باند (BW) بین فرکانسهای قطع منفی 3 دسیبل بالا و پایین است و شکل زیر توضیح مختصری در این باره دارد:
پس برای مثال ساده ما در بالا، اگر پهنای باند یا fH – fL 400 هرتز باشد و فرکانس مرکزی fr برابر با 346 هرتز باشد، پس در نتیجه ضریب کیفیت فیلتر به این صورت خواهد بود:
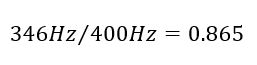
× توجه کنید که ضریب Q فقط یک عدد است و واحدی ندارد ×
هنگام تجزیه و تحلیل فیلترهای اکتیو، به طور کلی یک مدار نرمال شده در نظر گرفته میشود که یک پاسخ فرکانسی «ایده آل» به شکل مستطیل، با یک انتقال بین باند عبور و باند توقف دارای یک شیب ناگهانی یا بسیار تند ایجاد میکند. با این حال، این پاسخهای ایدهآل در دنیای واقعی امکانپذیر نیستند، بنابراین ما از تقریبها استفاده میکنیم تا بهترین پاسخ فرکانسی ممکن را برای نوع فیلتری که میخواهیم طراحی کنیم، ارائه دهیم.
احتمالا شناختهشدهترین تقریب فیلتر برای انجام این کار، فیلتر باترورث یا صافترین پاسخ ممکن است. در مقاله بعدی نگاهی بر فیلترهای درجه بالاتر میاندازیم و از تقریبهای باترورث برای تولید فیلترهایی استفاده میکنیم که دارای پاسخ فرکانسی تا حد امکان از نظر ریاضی در باند عبور مسطح هستند و شیب انتقال کندی دارند.