جدول درستی برای هر عملکرد منطقی
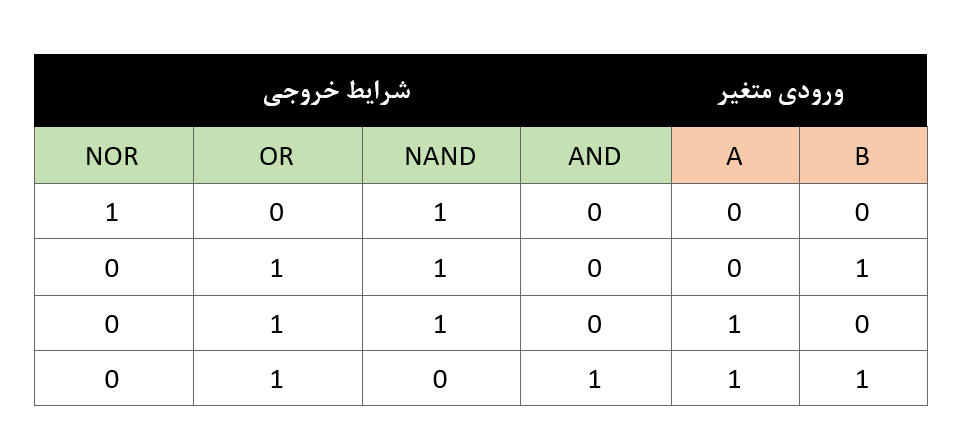
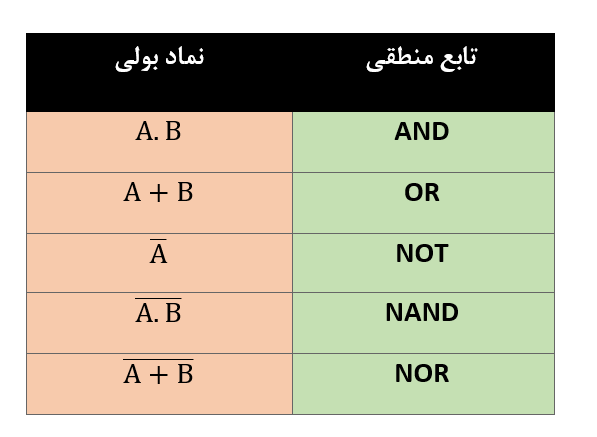
جدول زیر، لیستی از توابع منطقی معروف و نیز نماد بولی معادل آنها، را به ما میدهد. در این لیست یک “.” (یک نقطه) به معنای عملکرد (حاصلضرب) AND، یک “+” (نماد بهعلاوه) بهمعنای عملکرد (جمع) OR است و مکمل یا معکوس یک متغیر، با علامت بار (خط) روی متغیر نشان داده میشود.
قضیهی دمورگان
قضیههای دمورگان، اساسا دو مجموعه از قواعد و قوانین میباشند؛ که از عبارات بولی برای گیتهای AND، OR و NOT با استفاده از دو متغیر ورودی A و B ساخته شدهاند. این قوانین یا تئوریها، اجازه میدهند؛ تا متغیرهای ورودی، منفی شده و از یک شکل تابع بولی به شکل مخالف آن، تبدیل شوند.
قضیهی اول دمورگان، بیان میکند؛ که دو (یا چند) متغیر، اگر با یکدیگر NOR شوند؛ برابر با این است که این دو متغیر، معکوسشده (مکمل) و سپس باهم AND شوند. از طرف دیگر، قضیهی دوم دمورگان، بر این بیان استوار است؛ که دو (یا چند) متغیر، اگر با یکدیگر NAND شوند؛ همانند این است که این دو متغیر معکوسشده (مکمل) و سپس باهم OR شوند. به این معنا، که تمام عملگرهای OR با عملگرهای AND و تمام عملگرهای AND با OR جایگزین شوند.
قضیهی اول دمورگان
قضیهی اول دمورگان، ثابت میکند؛ که وقتی دو ( یا تعداد بیشتری) متغیر ورودی با یکدیگر AND شده و سپس معکوس شوند؛ معادل OR کردن مکملهای این متغیرهای منفرد با یکدیگر است.
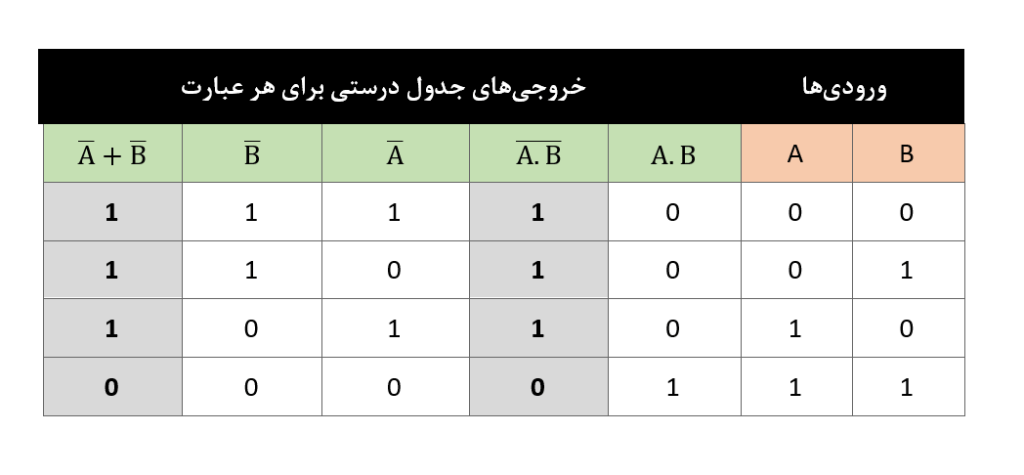
بنابراین، معادل تابع NAND، برابر با تابع منفی-OR است و عبارات زیر را ثابت میکند. این عملکرد را میتوانیم با استفاده از جدول زیر نمایش دهیم.
اعتبارسنجی قضیهی اول دمورگان با استفاده از جدول درستی
پیادهسازی قضیهی اول دمورگان با استفاده از گیتهای منطقی
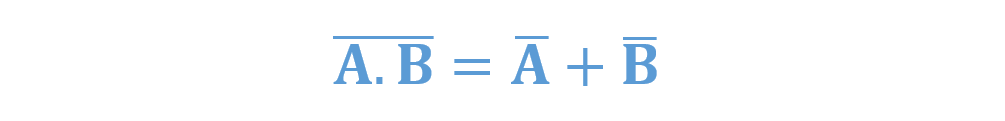
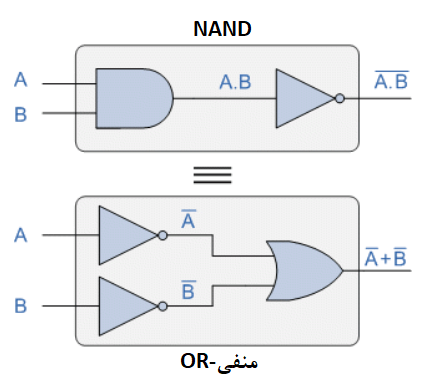
گیت منطقی بالا، چیدمانی از A.B (بار) را نشان میدهد؛ که میتواند با استفاده از گیت NAND و دو ورودی A و B پیادهسازی شود. در چیدمان گیت منطقی پایین، ابتدا دو ورودی معکوس شده و سبب ایجاد A (بار) و B (بار) میشوند. این دو، سپس بهعنوان ورودیهای گیت OR خواهندبود. بنابراین، خروجی گیت OR، برابر با A (بار) + B (بار) میشود.
دراینجا میتوانیم ببینیم؛ که تابع گیت استاندارد OR با داشتن وارونسازها (گیت NOT) در هر ورودی، معادل تابع گیت NAND است. پس یک گیت NAND تنها را، میتوان از این طریق، بهعنوان هم ارز منفی -OR نشان داد.
قضیهی دوم دمورگان
قضیهی دوم دمورگان، ثابت میکند؛ که وقتی دو (یا تعداد بیشتری) متغیر ورودی با یکدیگر OR شده و سپس معکوس شوند؛ معادل AND کردن مکملهای این متغیرهای منفرد با یکدیگر است.
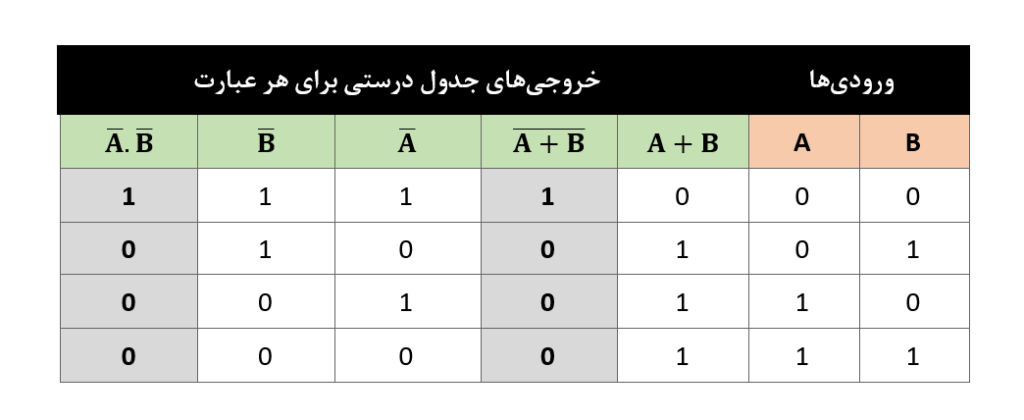
بنابراین، معادل تابع NOR، برابر با تابع منفی-AND است و عبارت زیر را ثابت میکند. این عملکرد را میتوانیم با استفاده از جدول زیر نمایش دهیم.
اعتبارسنجی قضیهی دوم دمورگان با استفاده از جدول درستی
پیادهسازی قضیهی دوم دمورگان با استفاده از گیتهای منطقی
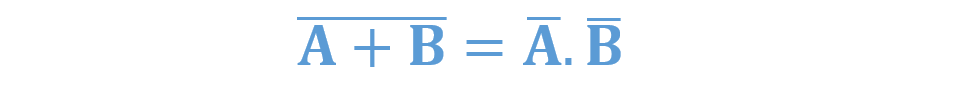
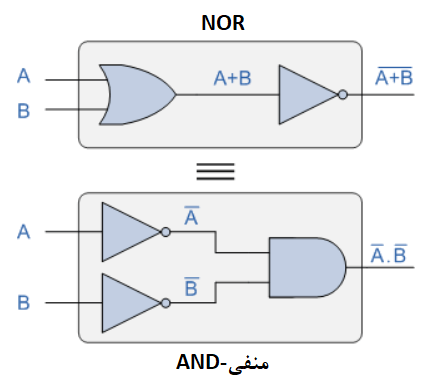
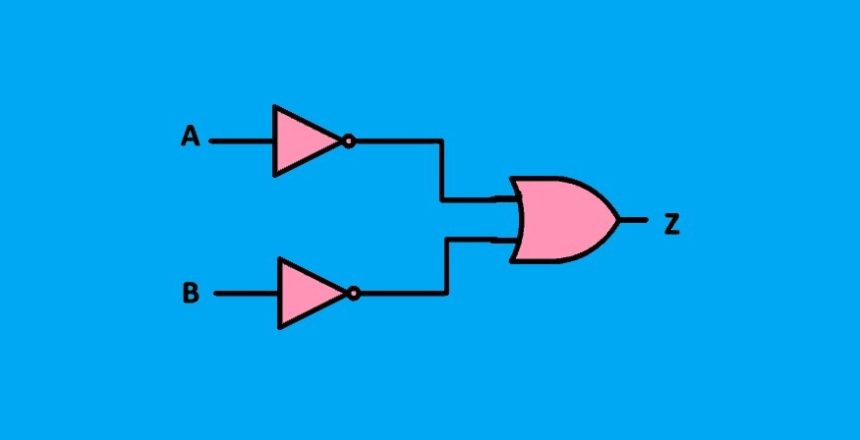
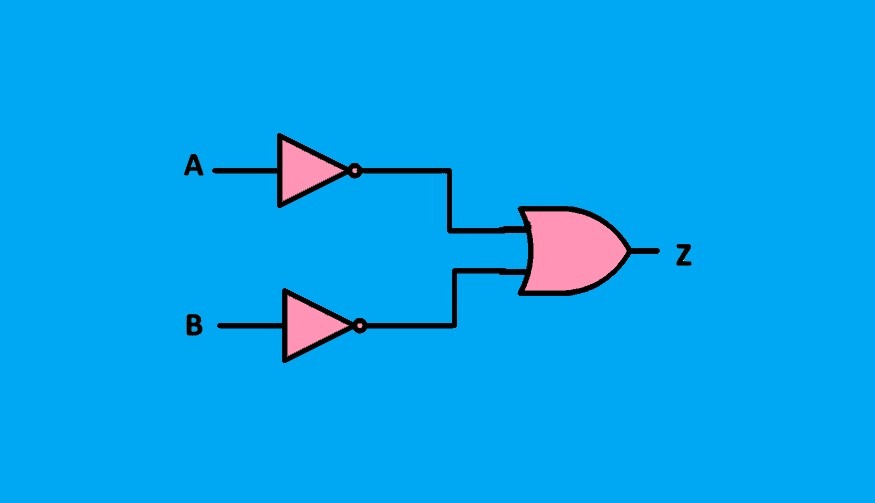
گیت منطقی بالا، آرایشی از A+B (بار) را نشان میدهد؛ که میتواند با استفاده از گیت NOR و دو ورودی A و B پیادهسازی شود. در آرایش گیت منطقی پایین، ابتدا دو ورودی معکوس شده A (بار) و B (بار) ایجاد میشوند. و سپس بهعنوان ورودیهای گیت AND عمل میکنند. بنابراین، خروجی گیت AND، برابر با A (بار) . B (بار) میشود.
دراینجا میتوانیم ببینیم؛ که تابع گیت استاندارد AND با داشتن وارونسازها (گیت NOT) در هر ورودی، شرط خروجی معادل را برای تابع استاندارد گیت NOR تولید میکند و هر گیت NAND تنها، میتواند از این طریق بهعنوان هم ارز منفی-AND نشان دادهشود.
با وجود اینکه ما قضیههای دمورگان را برای تنها دو متغیر ورودی A و B بهکار بردیم؛ آنها کاملا برای عبارات متغیر با سه، چهار یا تعداد بیشتری ورودی، معتبر هستند. برای مثال:
برای یک ورودی 3 متغیره،
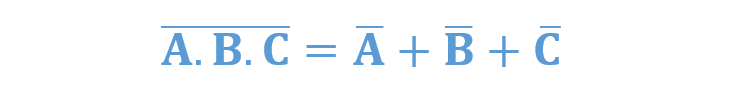
و همچنین،
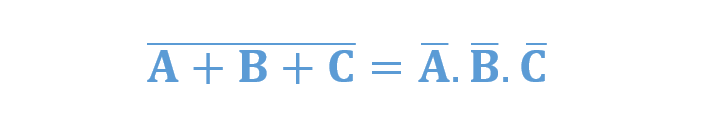
برای یک ورودی 4 متغیره،
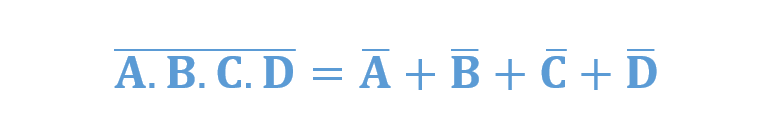
و نیز،
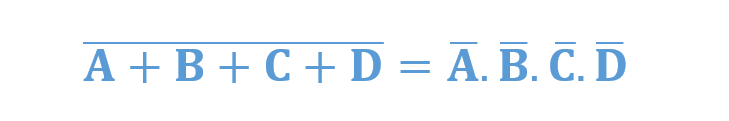
و به همین ترتیب، ادامه خواهیم داد.
گیتهای معادل دمورگان
در اینجا دیدیم؛ که با استفاده از تئوریهای دمورگان، میتوان عملگرهای AND (.) را با OR (+) و نیز برعکس، جایگزین کرد و سپس، هر ترم یا متغیر را در هر عبارتی با استفاده از معکوسکردن آن، مکمل کرد؛ یعنی پیش از معکوسکردن کل تابع 0 را به 1 و 1 را به 0، تبدیل کرد.
بنابراین، برای بدستآوردن معادل برای گیت AND ،NAND ، OR یا NOR، بهسادگی میتوان وارونسازها (گیتهای NOT ) به همهی ورودیها و خروجیها اضافه کرد و نماد AND را به نماد OR و یا نماد OR را به نماد AND را تغییر داد؛ همانگونه که در جدول زیر آمدهاست.
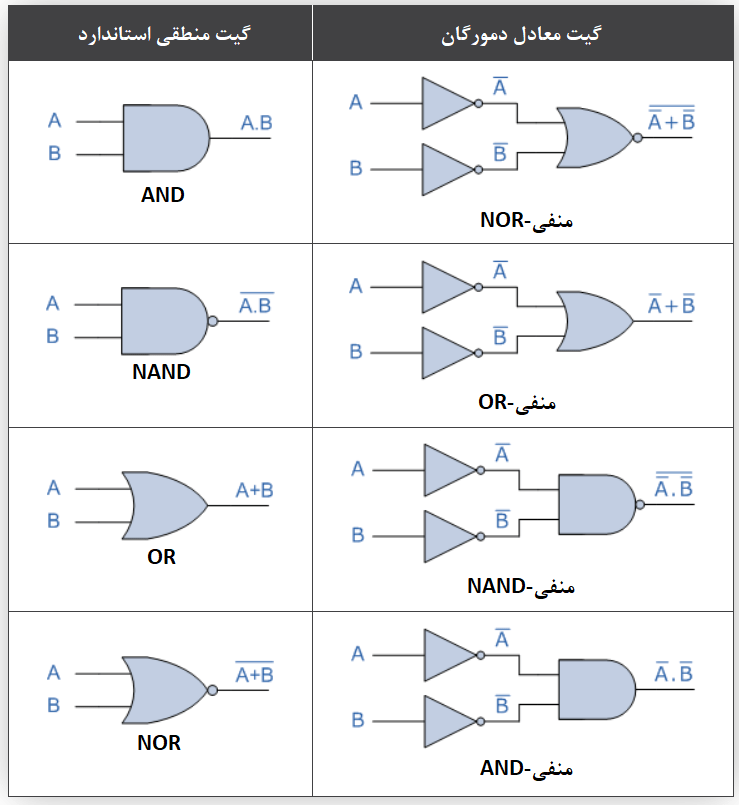
بنابراین بر اساس تئوری دمورگان: مکمل دو (یا تعداد بیشتری) متغیر ورودی ANDشده با یکدیگر، معادل OR نمودن مکملهای این متغیرهاست و نیز، مکمل دو (یا تعداد بیشتری) متغیر ورودی OR شده با یکدیگر، معادل AND نمودن مکملهای این متغیرهاست؛ که توسط دمورگان تعریف میشود.