اعداد مختلط و فازور ها. ریاضیاتی که در مهندسی برق، برای جمعکردن مقاومتها، جریانها یا ولتاژهای DC استفاده میشود؛ از آنچه که “اعداد حقیقی” نامیده میشود؛ به عنوان اعداد صحیح یا کسر استفاده میکند.
اما اعداد حقیقی، تنها نوع اعداد مورد استفاده نیستند؛ خصوصا هنگامی که با منابع سینوسی و بردارها سر و کار داریم. علاوه بر استفاده از اعداد نرمال یا حقیقی، اعداد مختلط برای حل معادلات مختلط یا اعدادی که ریشههای مربع اعداد منفی 1√- میباشند، معرفی شدند.
در مهندسی برق، به این نوع از اعداد، “اعداد موهومی” گفته میشود و برای تمایز یک عدد موهومی از یک عدد حقیقی، از حرف انگلیسی “j” که معمولا در مهندسی برق به عنوان عملگر “j “ معروف است، استفاده میشود. بنابراین، حرف “j” در مقابل یک عدد حقیقی قرار میگیرد تا نشاندهندهی عملکرد یک عدد موهومی باشد.
مثالهایی از اعداد موهومی، عبارتند از: j3، j12 و j100 و غیره. درنتیجه، یک عدد مختلط، از دو قسمت متمایز اما کاملا مرتبط با هم یک “عدد حقیقی” بهعلاوه یک “عدد موهومی” تشکیل شدهاست.
اعداد مختلط، نشان دهندهی نقاطی در یک مجموعه دو بعدی یا صفحه s میباشند؛ که به دو محور مجزا ارجاع داده میشوند. محور افقی را “محور حقیقی” و محور عمودی را “محور موهومی” مینامند. بخشهای حقیقی و موهومی یک عدد مختلط، به ترتیب با نماد Re(z) و Im(z) نمایش داده میشوند.
اعداد مختلطی را که از اعداد حقیقی (مولفهی فعال) و موهومی (مولفهی انفعالی) تشکیل شدهاند؛ میتوان جمع کرد یا تفریق نمود یا دقیقا به همان روشی که برای تجزیه و تحلیل مدارهای DC از جبر ابتدایی استفاده میشود، از آن استفاده نمود.
قواعد و قوانینی که در ریاضیات برای جمع و تفریق نمودن اعداد موهومی استفاده میگردد؛ همانند اعداد حقیقی (j2+j4=j6) و … است. تنها تفاوت موجود درضرب آنها است؛ زیرا دو عدد موهومی، با ضرب شدن در یکدیگر، به یک عدد حقیقی منفی تبدیل میشوند. اعداد حقیقی را، میتوان به عنوان یک عدد مختلط در نظر گرفت ؛که دارای یک بخش موهومی با برچسب j0 میباشند.
مقدار عملگر j، دقیقا برابر با 1√ – است؛ بنابراین ضرب پیدرپی j”(j*j)” منجر به مقدار 1- و “j-” منجر به مقدار 1+ میگردد. عملگر j، معمولا برای نشاندادن دوران برخلاف عقربه های ساعت استفاده میگردد، در نتیجه، هر ضرب یا توان j ” ،j2 ،j3 “ و… بردار را وادار میکند تا در جهت مخالف عقربههای ساعت با زاویه ثابت °90 دوران یابد که در زیر نشان داده شده است. به همین ترتیب، اگر ضرب بردار، ناشی از عملگر j- باشد؛ تغییر فاز °90- خواهد بود که به معنی دوران در جهت عقربههای ساعت است.
دوران برداری اپراتور j
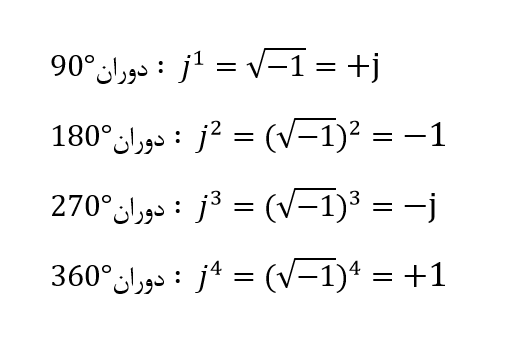
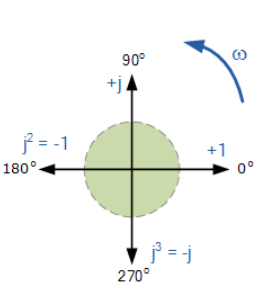
بنابراین، ضرب یک عدد موهومی با j2، سبب °180 دوران برخلاف جهت عقربههای ساعت، با ضرب با j3، دوران °270 و با j4 دوران °360 را خواهد داشت و در نهایت به موقعیت اصلی خود باز میگردد. ضرب با j10 یا j30 سبب دوران بردار بر خلاف جهت عقربههای ساعت به میزان مناسب میگردد. در هر دوران متوالی، اندازه بردار همیشه ثابت است.
در مهندسی برق، روشهای مختلفی وجود دارد؛ که میتواند یک عدد مختلط را به صورت گرافیکی یا ریاضی نشان داد. یکی از روشهایی که از قاعدهی کسینوسی یا سینوسی استفاده میکند؛ فرم کارتزین یا دکارتی است.
اعداد مختلط با استفاده از فرم مستطیلی
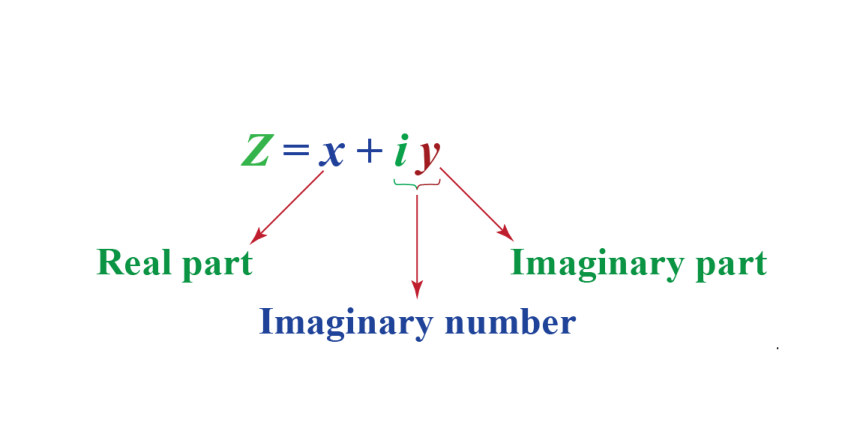
در آخرین مقاله مرتبط با فازورها، دیدیم که یک عدد مختلط، با یک بخش حقیقی و یک بخش موهومی نشان داده میشود، که شکل تعمیم یافته آن به صورت زیر است:
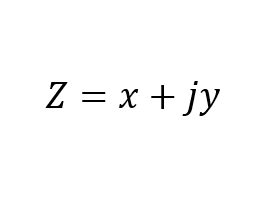
در جایی که:
Z : یک عدد مختلط است که نشاندهندهی بردار است.
x : بخش حقیقی یا جز فعال.
y : بخش موهومی یا جز انفعالی.
j : توسط √-1 تعریف میشود.
در فرم دکارتی، یک عدد مختلط را میتوان، به عنوان یک نقطه در یک صفحه مختلط یا s نشان داد. بنابراین به عنوان مثال Z=6+j4، یک نقطه واحد را نشان میدهد؛ که مختصات آن، 6 را در محور حقیقی افقی و 4 را در محور موهومی عمودی، نشان میدهد. همانطور که در تصویر زیر نشان داده شدهاست.
اعداد مختلط با استفاده از صفحه مختلط یا s
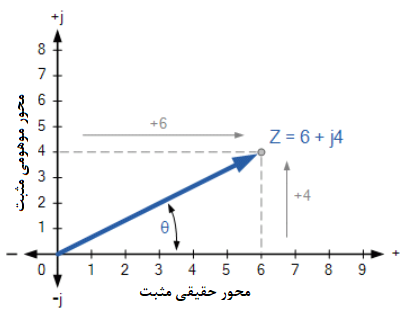
اما از آنجایی که، هر دو بخش حقیقی و موهومی یک عدد مختلط در فرم دکارتی، میتواند یک عدد مثبت یا یک عدد منفی باشد، بنابراین دو محور حقیقی و موهومی باید در دو جهت مثبت و منفی گسترش یابند. درنتیجه سبب ایجاد یک صفحه مختلط با چهار ربع، به نام نمودار آرگان ( Argand Diagram) میشود که در زیر آورده شده است.
نمودار چهار ربع Argand
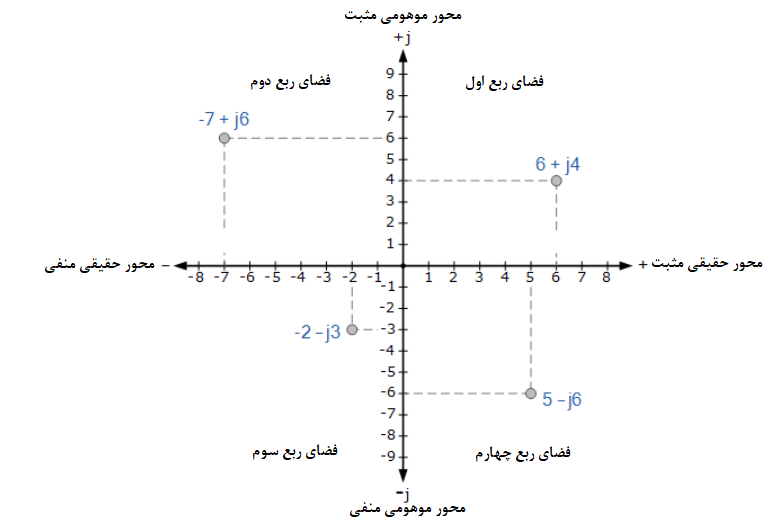
در نمودار Argand، محور افقی نشاندهنده تمام اعداد حقیقی مثبت، در سمت راست محور موهومی عمودی و تمام اعداد حقیقی منفی، در سمت چپ محور موهومی عمودی است. تمام اعداد موهومی مثبت در بالای محور افقی نشان داده میشوند؛ در حالیکه تمام اعداد موهومی منفی در زیر محور حقیقی افقی قرار دارند. سپس یک صفحه مختلط دو بعدی با چهار ربع مجزا با برچسب QI، QII، QIII و QIV تولید میشود.
از نمودار Argand فوق ، میتوان برای نشاندادن یک فازور دوار به عنوان یک نقطه در صفحه مختلط استفاده کرد؛ که شعاع آن با اندازه فازور ذکر میشود و برای هر 2π/ω ثانیه، یک دایره کامل، به دور خود میکشد.
سپس میتوانیم، این ایده را بیشتر گسترش دهیم؛ تا تعریف عدد مختلط را به صورت قطبی و دکارتی برای دورانهای °90 نشان دهیم.
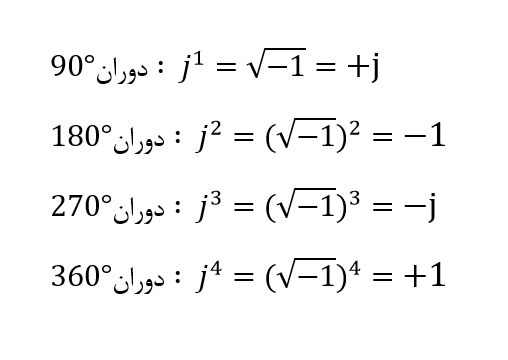
اعداد مختلط، همچنین میتوانند دارای بخشهای حقیقی یا موهومی “صفر” مانند Z=6+j0 یا Z=0+j4 باشند. در این حالت، نقاط به طور مستقیم روی محور حقیقی یا موهومی رسم میشوند. همچنین، میتوان زاویه اعداد مختلط را، با استفاده از مثلثات ساده، برای محاسبهی زاویههای مثلثهای قائم الزاویه محاسبه کرد، یا آن را در جهت عقربههای ساعت در اطراف نمودار Argand اندازهگیری کرد که از محور حقیقی مثبت شروع میشود. سپس زاویههای بین 0 تا 90° در ربع اول(I) و زاویههای (θ) بین 90° تا 180° در ربع دوم (II) قرار میگیرند. ربع سوم (III) شامل زاویههایی بین °180° تا °270 است؛ در حالیکه ربع چهارم و آخر (IV) که دایره را کامل میکنند، شامل زاویههای بین °270 تا °360 و غیره است. در هر چهار ربع زوایای مربوطه را میتوان از رابطه زیر یافت:

جمع و تفریق اعداد مختلط
جمع یا تفریق اعداد مختلط را، میتوان به صورت ریاضی یا گرافیکی به فرم مستطیلی انجام داد. علاوه بر این، ابتدا بخشهای حقیقی با هم جمع میشوند تا بخش حقیقی حاصلجمع را تشکیل دهند و سپس بخشهای موهومی، تا بخش موهومی حاصلجمع را تشکیل دهند و این فرآیند با استفاده از دو عدد مختلط A و B بهعنوان مثال به شرح زیر است.
جمع و تفریق مختلط
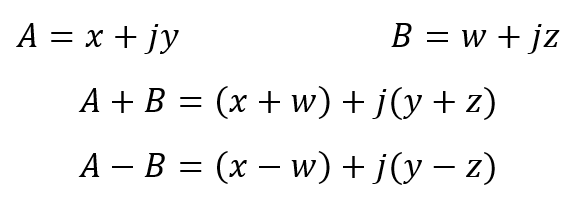
مثال شماره 1
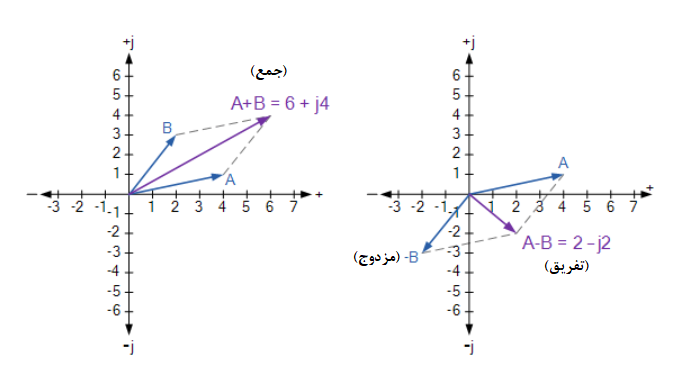
دو بردار و به ترتیب، تعریف میشوند. جمع و تفریق دو بردار را به دو فرم مستطیلی ( ) و به فرم گرافیکی به عنوان نمودار Argand تعیین کنید.
جمع و تفریق ریاضی
جمع
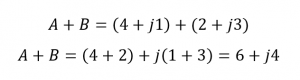
تفریق
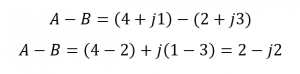
جمع و تفریق گرافیکی
ضرب و تقسیم اعداد مختلط
ضرب اعداد مختلط در فرم دکارتی، کم و بیش همان قوانین جبر عادی را همراه با چند قانون اضافی برای ضرب پیدرپی عملگر j دنبال میکند؛ در جاییکه j2= -1 است. به عنوان مثال، ضربکردن دو بردار بالا: A = 4 + j1 و B = 2 + j3 ، نتیجه زیر را به ما میدهد:
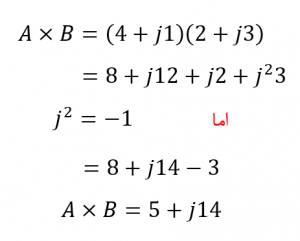
از نظر ریاضی، انجام تقسیم اعداد مختلط به فرم دکارتی، کمی دشوارتر است؛ زیرا برای تبدیل مخرج معادله، به یک عدد حقیقی، نیاز به استفاده از تابع مزدوج مخرج است به این عمل “منطقیسازی” گفته میشود. اما برای تقسیم اعداد مختلط بهتر است که از “فرم قطبی” استفاده شود که بعدا به آن خواهیم پرداخت. اما با این حال، به عنوان مثال، در فرم دکارتی، مقدار بردار A تقسیم بر بردار B را پیدا کنیم.
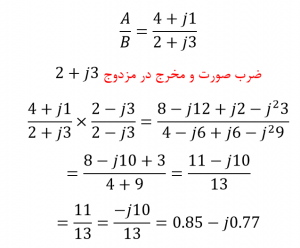
مزدوج مختلط
مزدوج مختلط، یا صرفا مزدوج یک عدد مختلط، تنها با معکوس کردن علامت جبری عدد مختلط حاصل میشود، در این حالت، علامت جبری عدد حقیقی را یکسان نگه داشته و برای شناسایی مزدوج مختلط z، از نماد استفاده میشود. برای مثال، مزدوج z = 6 – j4 ، z = 6 + j4 است؛ همانطور که مزدوج z = 6 + j4 ، z = 6 – j4 است.
نقاط موجود در نمودار Argand برای یک مزدوج مختلط، دارای همان موقعیت افقی در محور حقیقی با عدد مختلط اصلی است، اما در مقابل موقعیتهای عمودی قرار دارند. بنابراین، مزدوجهای مختلط را میتوان بازتابی از یک عدد مختلط دانست. مثال زیر یک عدد مختلط، 6+j4 و مزدوج آن را در صفحه مختلط نشان میدهد.
مزدوج اعداد مختلط
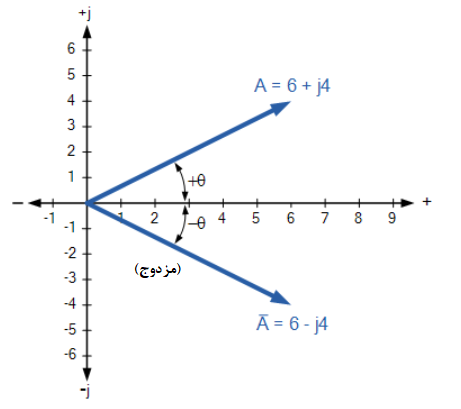
مجموع یک عدد مختلط و مزدوج مختلط آن، همیشه آنگونه که در بالا مشاهده نمودیم، یک عدد حقیقی خواهد بود. از اینرو، جمع یک عدد مختلط با مزدوج خود، فقط به عنوان یک عدد حقیقی یا مولفه فعال است؛ در حالیکه، تفریق آنها برابر با یک عدد موهومی یا مولفهی انفعالی میباشد. مزدوج یک عدد مختلط، عنصر مهمی در مهندسی برق است؛ برای تعیین توان ظاهری مدار AC با استفاده از فرم دکارتی استفاده میشود.
اعداد مختلط با استفاده از فرم قطبی
برخلاف فرم دکارتیکه نقاط را در صفحهی مختلط، رسم میکند؛ فرم قطبی عدد مختلط، با اندازه و زاویه نوشته میشود. بنابراین، یک بردار فرم قطبی به این صورت ارائه میشود: در جاییکه، Z عدد مختلط به شکلقطبی است، A اندازه یا مدول برداری است و θ زاویه یا آرگومان A بوده که میتواند مثبت یا منفی باشد. اندازه و زاویه نقطه، همچنان به همان فرم مستطیل شکل باقی مانده است، اینبار محل نقطه به صورت قطبی به “فرم مثلثی” در زیر نشان داده شدهاست.
فرم قطبی نمایش اعداد مختلط
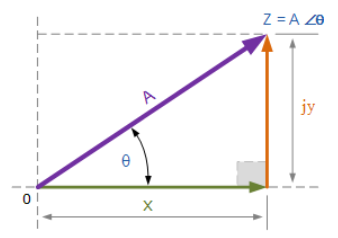
از آنجایی که نمایش قطبی یک نقطه بر اساس فرم مثلثی بنا شده است؛ ما میتوانیم از هندسه ساده مثلث به ویژه مثلثات و قضیه فیثاغورث در مثلثها استفاده کنیم تا هم اندازه و هم زاویه عدد مختلط را پیدا کنیم. همانگونه که از مدرسه به یاد میآوریم، مثلثات با رابطه بین اضلاع و زاویههای مثلث، سروکار دارد. بنابراین میتوانیم روابط بین اضلاع را به صورت زیر توصیف کنیم:
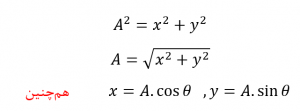
با استفاده دوباره از مثلثات، زاویه θ از A، به صورت زیر داریم:
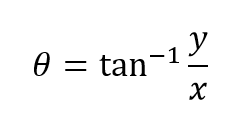
درنتیجه، در فرم قطبی، طول A و زاویهی آن، بهجای یک نقطه، عدد مختلط را نشان میدهد. همچنین در فرم قطبی، مزدوج عدد مختلط دارای اندازه یا مدول یکسانی است و علامت زاویه است که تغییر مینماید. درنتیجه برای مثال مزدوج 6 ∠30o برابر با 6 ∠– 30o است.
تبدیل بین فرم مستطیلی و فرم قطبی
در فرم دکارتی، میتوان یک بردار را از لحاظ مختصات مستطیلشکل بیان کرد، در حالیکه محور افقی محور حقیقی بوده و محور عمودی، محور موهومی و مولفهی j آن است. در شکل قطبی، این محورهای حقیقی و موهومی به سادگی به صورت A∠θ نشان داده میشود. با استفاده از مثال بالا، رابطه بین فرم دکارتی و قطبی را میتوان به صورت زیر تعریف نمود.
تبدیل فرم قطبی به فرم دکارتی (P→R)

همچنین، میتوانیم از فرم دکارتی به فرم قطبی به صورت زیر برگردیم:
تبدیل فرم دکارتی به فرم قطبی (R→P)

ضرب و تقسیم فرم قطبی
فرم مستطیلی، برای جمع و تفریق کردن اعداد مختلط، همانطور که در بالا دیدیم، بهترین است؛ اما فرم قطبی، غالبا برای ضرب و تقسیم بهتر است. برای ضرب دو بردار، به صورت قطبی، ابتدا باید دو مدول یا اندازه را باهم ضرب کرده و سپس زاویه های آنها را باهم جمع کنیم.
ضرب فرم قطبی
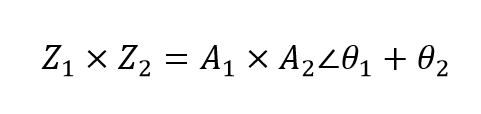
ضرب 6 ∠30o و 8 ∠– 45o به عنوان مثال به ما میدهد:
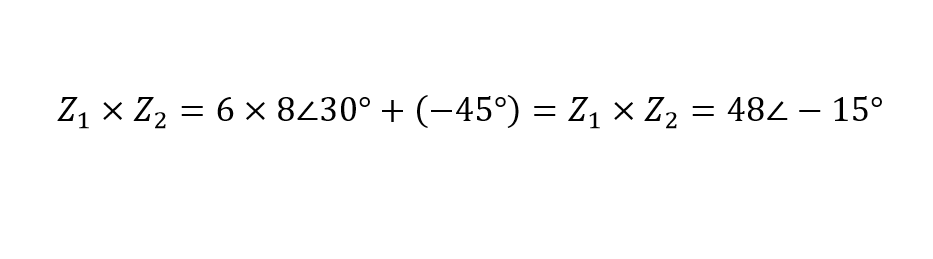
تقسیم فرم قطبی
به همینترتیب، برای تقسیم دو بردار به فرم قطبی، باید دو مدول را تقسیم کرده و سپس زاویههای آنها را از هم کم کنیم.
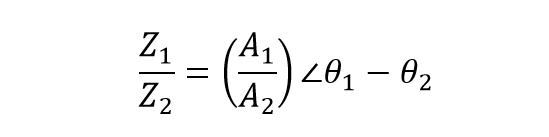
به عنوان مثال تقسیم 6 ∠30o و 8 ∠– 45o به ما میدهد:
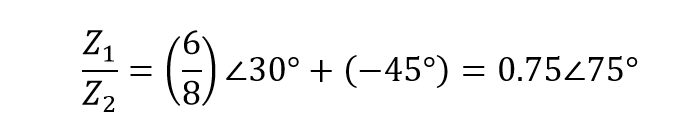
خوشبختانه، ماشینحسابهای مدرن علمی امروزی، توابع ریاضیاتی را ایجاد کردهاند که امکان تبدیل آسان از فرم دکارتی به قطبی ( R → P ) و بازگشت از فرم قطبی به دکارتی ( R → P ) را فراهم میکند.
اعداد مختلط با استفاده از فرم نمایی
تاکنون، اعداد مختلط را در فرم دکارتی ( a + jb ) و فرم قطبی ( A ∠±θ ) در نظر گرفتهایم. اما یک روش سوم برای نمایش یک عدد مختلط، وجود دارد که شبیه فرم قطبی است که با طول (بزرگی) و زاویه فاز موج سینوسی مطابقت دارد اما از پایه لگاریتم طبیعی …e = 2.718 281 برای یافتن مقدار عدد مختلط استفاده مینماید. این روش سوم، فرم نمایی نامیده میشود.
فرم نمایی، از توابع مثلثاتی مقادیر سینوسی، سینوس (sin) و کسینوس (cos) یک مثلث زاویهدار است، برای تعریف نمایی مختلط، به عنوان نقطه دوران در صفحه مختلط استفاده میکند. فرم نمایی برای یافتن موقعیت نقطه براساس اتحاد اویلر، که به نام ریاضیدان سوئیسی، لئونارد اویلر نامگذاری شده است، استفاده میگردد و به صورت زیر ارائه میشود:
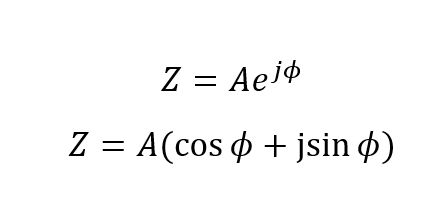
سپس اتحاد اویلر را میتوان با نمودار فازور دوار زیر در صفحه مختلط نشان داد.
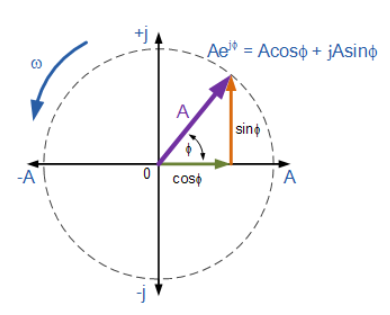
میتوانیم ببینیم که اتحاد اویلر بسیار شبیه فرم قطبی فوق است و به ما نشان میدهد که یک عدد مانند که دارای بزرگی 1 بوده، یک عدد پیچیده نیز است. میتوان اعداد مختلط را که به فرم نمایی میباشند به راحتی به فرم قطبی تبدیل کرد مانند: 2e j30 = 2∠30, 10e j120 = 10∠120 یا -6e j90 = -6∠90 . اتحاد اویلر، همچنین راهی برای تبدیل یک عدد مختلط از فرم نمایی به فرم دکارتی به ما میدهد. درنتیجه، رابطه بین فرم نمایی، قطبی و دکارتی در تعریف یک عدد مختلط آورده شدهاست.
فرمهای اعداد مختلط
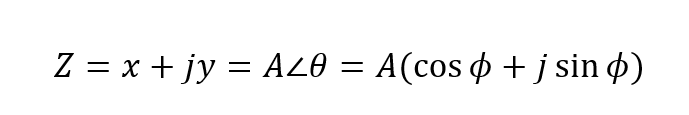
نماد فازور
تاکنون، به روشهای مختلفی، برای نشان دادن یک بردار دوار یا یک بردار ثابت؛ با استفاده از اعداد مختلط، برای تعریف یک نقطه در صفحه مختلط، نگاه کردهایم. نماد فازور، فرآیند ساختن یک عدد مختلط منفرد است؛ که دامنه و زاویه فاز شکلموج سینوسی داده شده را دارد.
سپس نماد فازور یا تبدیل فازور که گاهی اوقات، به این نام کاربرد دارد؛ سبب انتقال بخش حقیقی تابع سینوسی : A(t) = Am cos(ωt ± Φ) از حوزه زمان به حوزه عدد مختلط که دامنه فرکانس نیز نامیده میشود، میگردد.
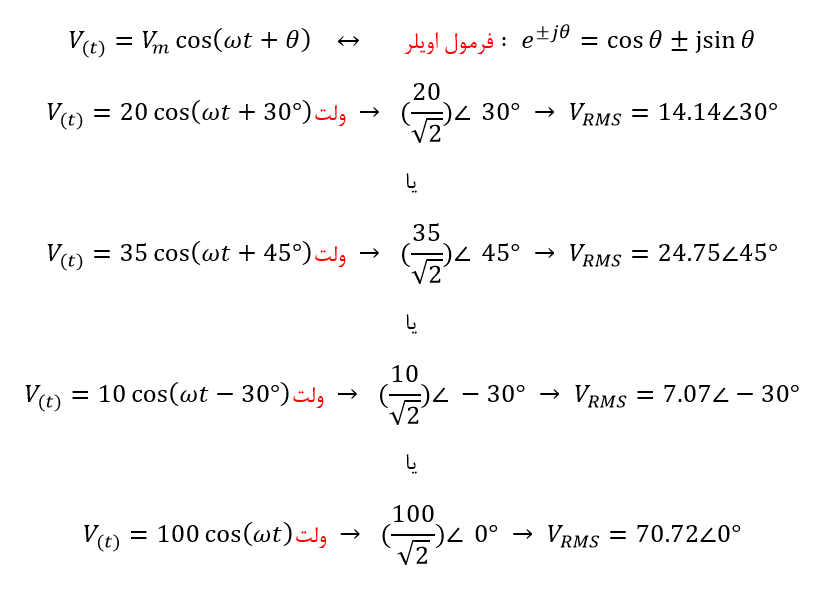
لطفا توجه داشته باشید، که 2√ حداکثر دامنه را به مقدار موثر یا RMS با زاویه داده شده بر حسب رادیان (ω) تبدیل میکند.
خلاصه اعداد مختلط
- اعداد مختلط، از دو عدد مجزا تشکیل شده اند: یک عدد حقیقی همراه با یک عدد موهومی.
- اعداد موهومی با استفاده از عملگر j ، از یک عدد حقیقی متمایز میشود.
- یک عدد با حرف ” j” در مقابل خود، مشخصکنندهی یک عدد موهومی در صفحه مختلط است.
- طبق تعریف: عملگر j ≡ √-1
- ضرب عملگر j در j برابر است با: j2 = -1
- فرم دکارتی یک عدد مختلط، با یک نقطه در فضای صفحه مختلط نشان داده میشود.
- در فرم قطبی، یک عدد مختلط با یک خط که طول آن، دامنه بوده و دارای زاویه فاز است؛ نشان داده میشود.
- در فرم نمایی یک عدد مختلط، با یک خط و زاویه مربوطه آن نشان داده میشود که از پایهی لگاریتم طبیعی استفاده میکند.
- یک عدد مختلط را میتوان، به یکی از سه روش زیر نشان داد:
فرم دکارتی: Z = x + jy
فرم قطبی: Z = A ∠Φ
فرم نمایی: Z = A e jΦ
- از اتحاد اویلر، میتوان برای تبدیل اعداد مختلط از شکل نمایی به دکارتی استفاده کرد.
در مقالات قبلی، از جمله همین مقاله، مشاهده شد که میتوان از فازورها برای نمایش شکلموجهای سینوسی استفاده کرده و دامنه و زاویه فاز آنها را میتوان به فرم یک عدد مختلط نوشت. همچنین دیده شد؛ که اعداد مختلط را، میتوان به فرم دکارتی، قطبی یا نمایی با تبدیل بین هر شکلی از جبر عدد مختلط، شامل، جمع، تفریق، ضرب و تقسیم ارائه کرد.
در چندمقاله بعدی، در ارتباط با رابطه فازور در مدارهای سری AC، به برخی اجزای پسیو (غیرفعال) مدار نگاه خواهیم کرد و نمودارهای فازور را برای جریان عبوری از جز مربوطه و ولتاژ اعمالشده به آن رسم خواهیم نمود و با مقاومت AC شروع خواهیم کرد.


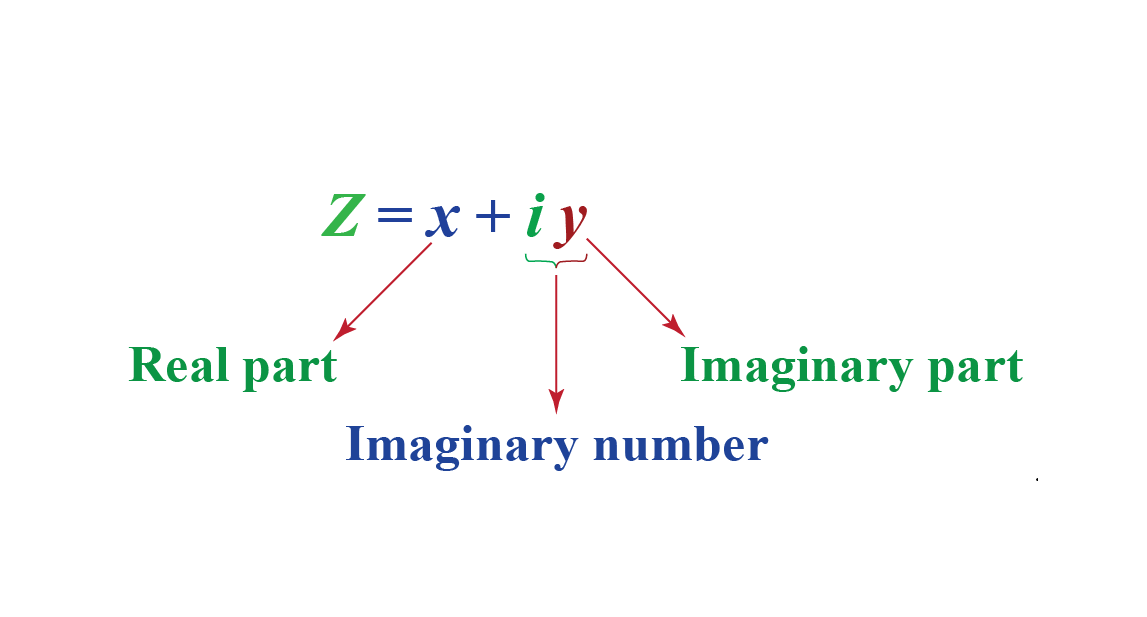




1 دیدگاه در “اعداد مختلط و فازورها”
خیلی خیلی سپاسگذارم
فوق العاده راحت و حرفه ای توضیح دادین
خیلی عالی بود
ممنون از زحماتتون