جبر بولی مجموعهای از قوانین و قواعد را بهکار میگیرد تا برای تعریف عملکرد مدار منطقی دیجیتال، از آنها استفاده شود.
همانطور که از نمادهای منطقی “0” و “1” برای نشاندادن یک ورودی یا خروجی دیجیتال، استفاده میشود؛ میتوانیم آنها را بهعنوان ثابت، بهترتیب برای مدارهای دائما “باز” یا “بسته” یا مدارهای اتصال (دارای کلید)، استفاده نماییم.
مجموعهای از قوانین و قواعد عبارات جبر بولی، بهعنوان کمککننده برای کاهش تعداد گیتهای منطقی موردنیاز برای انجام یک عملیات منطقی خاص ابداع شدهاند؛ که منجر به ایجاد فهرستی از توابع یا قضایا میشود؛ که معمولا بهعنوان قوانین جبر بولی شناخته میشوند.
جبر بولی، ریاضیات مورداستفاده برای آنالیز مدارها و گیتهای دیجیتال است. ما میتوانیم از این “قوانین بولی”، هم برای کاهش و هم سادهسازی عبارات بولی پیچیده، بهجهت کاهش تعداد گیتهای منطقی موردنیاز، استفاده کنیم. بنابراین، جبر بولی، سیستمی از ریاضیات مبتنی بر منطق است؛ که مجموعهای از قوانین و قواعد خاص خود را دارد؛ که برای تعریف و نیز کاهش عبارات بولی، استفاده میشود.
متغیرهایی که در جبر بولی استفاده میشوند؛ میتوانند تنها یکی از دو مقدار ممکنِ منطق “0” و منطق “1” را داشته باشند. اما یک عبارت، میتواند تعداد بینهایتی از متغیر را داشته باشد؛ که هر کدام بهصورت منحصربفرد، لیبل خوردهاند (برچسبگذاری شدهاند) تا ورودیهای یک عبارت را نشان دهند. برای مثال، متغیرهای A، B،C و …. به ما عبارت منطقی A+B=C را میدهند؛ اما هر متغیر میتواند تنها یک مقدار 0 یا 1 را اختیار کند.
مثالهایی از این قوانین منحصربفرد بولی، قواعد و تئوریهای جبر بولی در جدول زیر، آمدهاست.
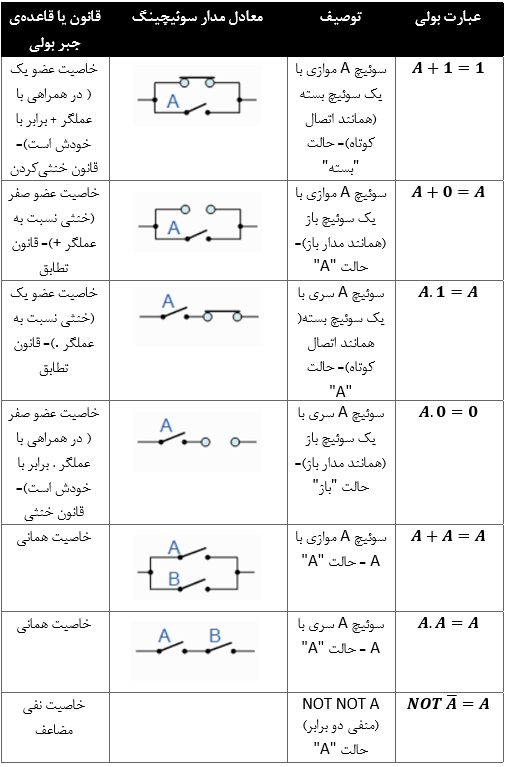
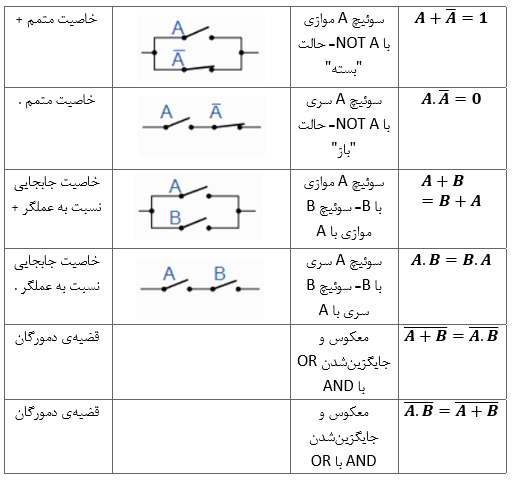
آن دسته از، قوانین پایهای جبر بولی، که مرتبط با قانون جابجایی است؛ به ما اجازهی تغییر موقعیت را برای جمع یا ضرب میدهد. همچنین قانون شرکتپذیری، حذف براکتها را برای جمع و ضرب مجاز میداند و در نهایت، با قانون توزیعپذیری، میتوانیم اجازهی فاکتورگرفتن یک عبارت را همانند جبر عادی داشته باشیم.
هر قانون بولی در جدول بالا، با دو یا یک متغیر آمدهاست؛ اما تعداد متغیرهایی که با یک قانون تنها تعریف میشوند؛ به این تعداد محدود نمیشود؛ بلکه میتواند بینهایت تعداد متغیر بهعنوان ورودیهای یک عبارت، وجود داشته باشد. قوانین بولی که در بالا توضیح داده شد؛ میتوانند برای اثبات هر عبارت بولی معین و همچنین برای سادهکردن مدارهای دیجیتال پیچیده، استفاده شوند.
در ادامه توضیح کوتاهی از تعدادی قوانین بولی به همراه A که نماد ورودی متغیر است؛ آورده شدهاست.
قوانین جبر بولی
قانون خنثیکردن (Annulment Law)
عبارت A، درصورت AND شدن با “0” برابر با صفر و درصورت OR شدن با “1” برابر با 1 است.
A.0 = 0 : متغیر A درصورت AND شدن با 0، همیشه برابر با 0 است.
A+1 = 1 : متغیر A درصورت OR شدن با 1، همیشه برابر با 1 است.
قانون تطابق (Identity Law)
عبارت A، درصورت OR شدن با “0” یا AND شدن با “1” برابر همیشه برابر با خودش است.
A+0 = A : متغیر A درصورت OR شدن با 0، همیشه برابر با خودش است.
A.1 = A : متغیر A درصورت AND شدن با 1، همیشه برابر با خودش است.
قانون همانی (Idempotent Law)
یک متغیر، درصورت AND شدن یا OR شدن با خودش، همیشه برابر با خود متغیر است.
A+A = A : متغیر A درصورت OR شدن با خودش، همیشه برابر با خودش است.
A.A = A: متغیر A درصورت AND شدن با خودش، همیشه برابر با خودش است.
قانون متمم (Complement Law)
متغیر A، درصورت AND شدن با مکمل خود برابر با “0” یا OR شدن مکمل خود برابر با “1” است.
1=A+Ā : متغیر A درصورت OR شدن با مکمل خود همیشه برابر با 1 است.
0=A.Ā : متغیر A درصورت AND شدن با مکمل خود همیشه برابر با 0 است.
قانون جابجایی (Commutative Law)
ترتیب عملکرد دو عبارت منحصربفرد، اهمیت ندارد.
A.B=B.A : ترتیب در دو متغیر که باهم AND شدهاند؛ تفاوتی ایجاد نمیکند.
A+B=B+A : ترتیب در دو متغیر که باهم AND شدهاند؛ تفاوتی ایجاد نمیکند.
قانون نفی مضاعف (Double Negation Law)
یک عبارت که دو بار معکوس شود؛ برابر با عبارت اصلی و اولیه است.
A ̿=A : دوبار مکمل نمودن یک متغیر، همیشه برابر با خود متغیر است.
قضیه دمورگان (de Morgan’s Theorem)
دو قانون یا قضیهی “دمورگان” وجود دارد:
- دو عبارت جداگانه که با یکدیگر NOR شوند؛ برابر با ابتدا معکوسشدن(متمم) و سپس AND شدن آنها با یکدیگر است. برای مثال:
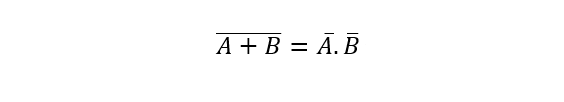
- دو عبارت جداگانه که با یکدیگر NAND شوند؛ برابر با ابتدا معکوسشدن(متمم) و سپس OR شدن آنها با یکدیگر است. برای مثال:
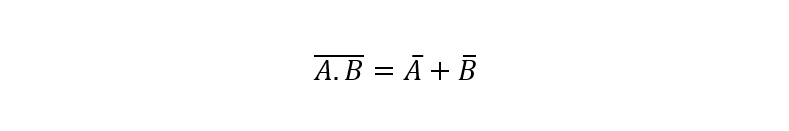
سایر قوانین بولی که جزئیات آن در بالا نیامده است؛ شامل:
مفروضات بولی:
با وجود آنکه جزو قوانین بولی نیستند؛ اما مجموعهای از قوانین ریاضیاتی میباشند؛ که میتوانند برای سادهسازی عبارات بولی، استفاده شوند.
0.0=0 : عدد صفر، هنگام AND شدن با خود، همیشه برابر با 0 است.
1.1=1 : عدد یک، هنگام AND شدن با خود، همیشه برابر با 1 است.
1.0=0 : عدد یک، هنگام AND شدن با صفر، همیشه برابر با 0 است.
0+0=0 : عدد صفر، هنگام OR شدن با خود، همیشه برابر با 0 است.
1+1=1 : عدد یک، هنگام OR شدن با خود، همیشه برابر با 1 است.
1+0=1 : عدد یک، هنگام OR شدن با صفر، همیشه برابر با 1 است.
0 ̅=1 : معکوس(متمم) عدد صفر، همیشه برابر با یک است.
1 ̅=0 : معکوس(متمم) عدد یک، همیشه برابر با صفر است.
قانون توزیعپذیری (Distributive Law)
بر اساس این قانون، ضرب و فاکتورگرفتن مجاز است.
A(B+C)=A.B+A.C : (قانون توزیعپذیری OR)
A+(B.C)=(A+B).(A+C) : (قانون توزیعپذیری AND)
قانون جذبی (Absorptive Law)
این قانون، با جذب عبارات مشابه به هم، یک عبارت پیچیده را به یک عبارت سادهتر، کاهش میدهد.
A+(A.B)=(A.1)+(A.B)=A(1+B)=A : (قانون جذبی OR)
A(A+B)=(A+1).(A+B)=A+(0.B)=A : (قانون جذبی AND)
قانون شرکتپذیری (Associative Law)
این قانون، حذف براکتها از عبارت و ترکیب مجدد متغیرها را مجاز میداند.
A+(B+C)=(A+B)+C=A+B+C : (قانون شرکتپذیری OR)
A.(B.C)=(A.B)C=A.B.C : (قانون شرکتپذیری AND)
توابع جبر بولی
با استفاده از اطلاعات بالا، گیتهای ساده و دو ورودی AND ، OR و NOT را میتوان با 16 تابع ممکن همانطور که در جدول زیر آمده است؛ نشان داد.
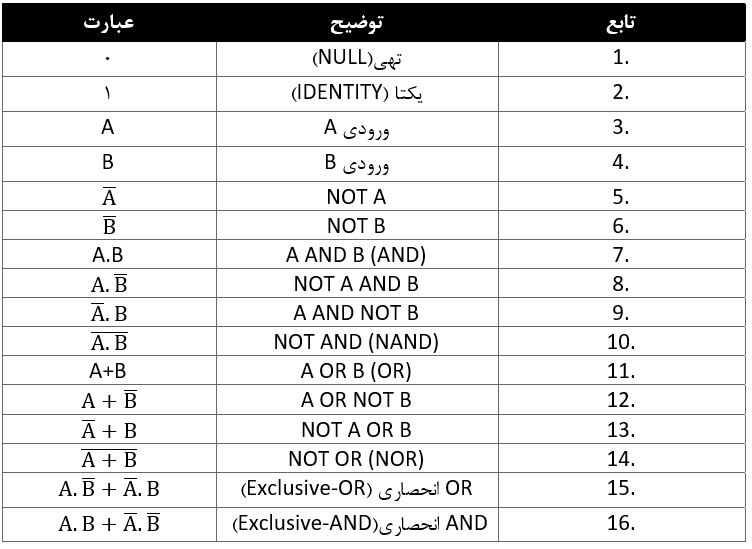
مثال شمارهی یک قوانین جبر بولی
با استفاده از قوانین بالا، عبارت روبرو را ساده کنید: (A+B)(A+C)

درنتیجه عبارت (A+B)(A+C) را میتوان با قانون توزیعپذیری به عبارت A+(B.C) ساده کرد.







