به عنوان مثال NAND مخالف گیت AND است یا NOR مخالف گیت OR هر کدام از این گیت ها را میتوان به یکدیگر متصل کرد تا مدارات منطقی ترکیبی و پیچیدهتری به دست بیاید .
همچنین در گذشته دیدیم که در الکترونیک دیجیتال هر دو گیت NAND و NOR گیت های همگانی (Universal) هستند به این معنا که با استفاده از این دو گیت میتوان بقیه گیتهای منطقی را نیز ساخت در حقیقت هر مدار ترکیبی میتواند تنها به وسیله دو یا گیت گیت NAND و NOR ساخته شود. همچنین متوجه شدیم که گیت NOR و بافرها المانهایی با ورودی تکی هستند که میتوانند خروجی امپدانس بالای ۳ حالته داشته باشند که از آن میتوان برای کنترل جریان اطلاعات در یک سیم اطلاعات باس (BUS) بهره برد .
گیتهای منطقی دیجیتال میتوانند با المان هایی همچون مقاومت ، ترانزیستور و دیود ساخته شوند تا یک RLT (Resistor_Transistor Logic) را به وجود بیاورند یا به صورت DTL (Diode_Transistor Logic) باشند اما امروزه مدارات مجتمع سری 74xxx با استفاده از TTL (Transistor_Transistor Logic) ساخته میشوند TTL متشکل از دو ترانزیستور دو قطبی NPN است یا اگر بخواهیم مدار مجتمع منطقی سریعتر با توان مصرفی کمتری داشه باشیم ، از ترانزیستورهای MOSFET (CMOS) استفاده میکنیم تراشه های سری 74Cxxx، 74HCxxx و سری 4000 در ساختارشان در CMOS بهره میبرند .
۸ عدد گیت منطقی دیجیتال استاندارد در زیر به همراه جدول درستیشان نشان داده شدهاند.
انواع گیت های منطقی دیجیتال
گیت AND
|
جدول درستی
|
||
|---|---|---|
|
Q
|
A
|
B
|
|
0
|
0
|
0
|
|
0
|
1
|
0
|
|
0
|
0
|
1
|
|
1
|
1
|
1
|
به صورت A AND B به ما Q را میدهد
نماد

عبارت بولی Q= A.B
گیت OR
|
جدول درستی
|
||
|---|---|---|
|
Q
|
A
|
B
|
|
0
|
0
|
0
|
|
1
|
1
|
0
|
|
1
|
0
|
1
|
|
1
|
1
|
1
|
به صورت A OR B به ما Q را میدهد
نماد
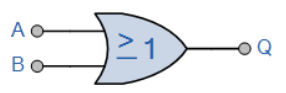
عبارت بولی Q= A+B
گیتهای منطقی معکوس کننده
گیت NAND
|
جدول درستی
|
||
|---|---|---|
|
Q
|
A
|
B
|
|
1
|
0
|
0
|
|
1
|
1
|
0
|
|
1
|
0
|
1
|
|
0
|
1
|
1
|
به صورت A AND B به ما NOT Q را میدهد
نماد
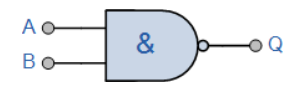
عبارت بولی ¯(Q= (A.B
گیت NOR
|
جدول درستی
|
||
|---|---|---|
|
Q
|
A
|
B
|
|
1
|
0
|
0
|
|
0
|
1
|
0
|
|
0
|
0
|
1
|
|
0
|
1
|
1
|
به صورت A OR B به ما NOT Q را میدهد
نماد

عبارت بولی ¯(Q= (A+B
گیتهای منطقی خاص
گیت XOR
|
جدول درستی
|
||
|---|---|---|
|
Q
|
A
|
B
|
|
0
|
0
|
0
|
|
1
|
1
|
0
|
|
1
|
0
|
1
|
|
0
|
1
|
1
|
به صورت A OR B اما NOT هردو به ما Q را میدهد
نماد
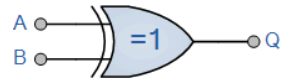
Q= A ⊕ B
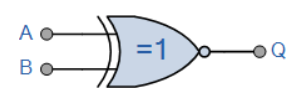
گیت XNOR
|
جدول درستی
|
||
|---|---|---|
|
Q
|
A
|
B
|
|
1
|
0
|
0
|
|
0
|
1
|
0
|
|
0
|
0
|
1
|
|
1
|
1
|
1
|
اگر B و A برابر باشند به ما خروجی Q را میدهد
نماد
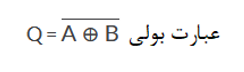
گیت های منطقی تک ورودی
بافر هگزا (The Hex Buffer)
|
جدول درستی
|
|
|---|---|
|
Q
|
A
|
|
0
|
0
|
|
1
|
1
|
به صورت A به ما Q را میدهد؛ خوانده میشود
نماد
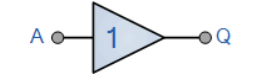
عبارت بولی Q = A
گیت معکوس کننده NOT
|
جدول درستی
|
||
|---|---|---|
|
Q
|
A
|
|
|
1
|
0
|
|
|
0
|
1
|
|
به صورت A معکوس به ما Q را میدهد
نماد
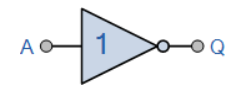
عبارت بولی ‾Q= not A or A
عملکرد گیت های منطقی بالا و منطق بولی شان میتواند در یک جدول به صورتی که در زیر نشان داده شده خلاصه گردد. این جدول رابطهی بین هر خروجی گیت منطقی دیجیتال را برای هر ترکیب ورودی ممکن نشان میدهد .
خلاصه جدول درستی گیت های منطقی دیجیتال
|
خروجی هر گیت به ازای ورودی های A و B
|
ورودی ها
|
||||||
|---|---|---|---|---|---|---|---|
|
XNOR
|
XOR
|
NOR
|
OR
|
NAND
|
AND
|
A
|
B
|
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
|
جدول درستی گیت های تک ورودی
|
||
|---|---|---|
|
Buffer
|
NOT
|
A
|
|
0
|
1
|
0
|
|
1
|
0
|
1
|
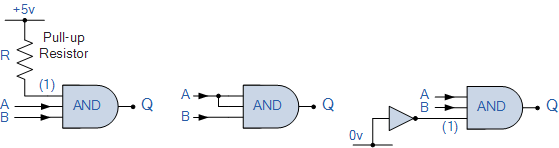
مقاومت pull-up و pull-down
آخرین نکتهای که ذکر آن خارج از لطف نیست این است که هنگامی که چند گیت منطقی دیجیتال را به یکدیگر متصل میکنید تا مدارهای منطقی به وجود بیاید؛ هر ورودی که به جایی وصل نیست باید به صورت مستقیم یا به سطح منطقی یک یا به سطح منطقی صفر متصل شود. برای این امر از مقاومت pull-up (پول آپ) یا pull-down (پول داون) استفاده میشود تا یک سیگنال ثابت منطقی ساخته شود. این روش از نوسانات ناخواستهی پایه گیت جلوگیری میکند و اجازه نمیدهد گیت، سیگنال سوییچینگ اشتباه تولید کند.
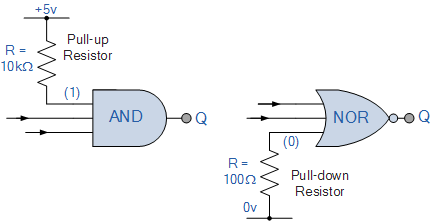
علاوه بر استفاده از مقاومت pull-up و pull-down به منظور جلوگیری از نوسان پایههای بلااستفاده گیتهای منطقی میتوان این پایههای بلااستفاده را به یکدیگر نیز متصل کرد برای درک بهتر به شکل زیر نگاه کنید: