تشدید، در مدار سری، زمانی اتفاق میافتد؛ که فرکانس منبع تغذیه، باعث شود ولتاژ در دو سر L و C برابر اما در فاز مخالف باشد.
تاکنون، رفتار یک مدار سری RLC را، که ولتاژ منبع آن، سینوسی حالت مانای فرکانس ثابت است؛ تجزیهوتحلیل کردهایم. ما همچنین در آموزش خود در مورد مدارهای سری RLC دیدهایم؛ که دو یا چند سیگنال سینوسی را میتوان با استفاده از فازورها ترکیب کرد، به شرطی که منبع تغذیه، فرکانس یکسانی برای همه، داشتهباشد. اگر ولتاژ تغذیهای با دامنهثابت اما با فرکانسهای مختلف، به مدار اعمال شود؛ چه اتفاقی برای مشخصات مدار میافتد؟!همچنین، رفتار پاسخ فرکانسی مدار، درصورت متغیر بودن فرکانس در دو عنصر راکتیو، چه خواهد بود؟!
در یک مدار سری RLC، نقطهی فرکانسی وجود دارد؛ که در آن راکتانس القایی سلف، از نظر مقداری با راکتانس خازنی خازن برابر گردد. به عبارتدیگر، XL=XC باشد. نقطهای که در آن، این اتفاق میافتد را نقطهی فرکانس تشدید ( fr ) یک مدار میگویند و از آنجاییکه ما درحال تجزیهوتحلیل یک مدار سری RLC میباشیم؛ این فرکانس تشدید، یک تشدید سری تولید مینماید.
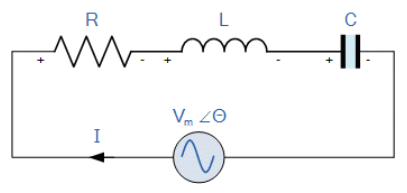
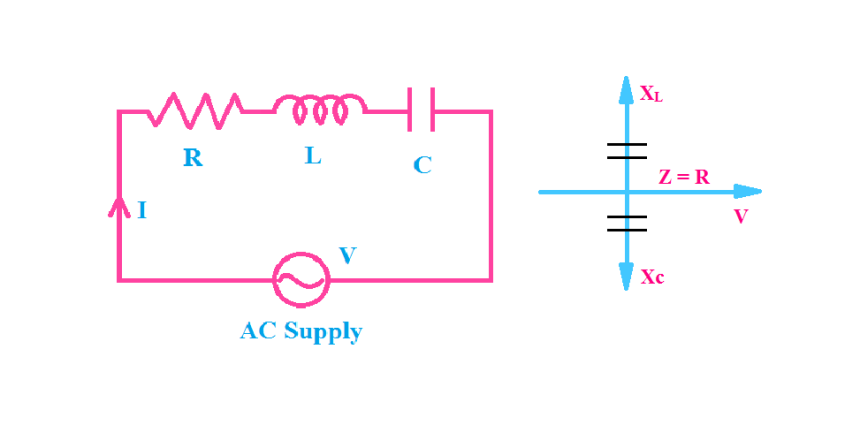
مدارهای تشدید سری، یکی از مهمترین مدارهای مورداستفاده در مدارهای الکتریکی و الکترونیکی میباشند؛ و میتوانند در شکلهای مختلفی از جمله، فیلترهای اصلی AC، فیلترهای نویز و همچنین، در مدارهای تنظیم رادیو و تلویزیون؛ که یک مدار تنظیم انتخابپذیر (Selective) برای دریافت کانالهای مختلف فرکانسی ایجاد میکند؛ یافت. مدار ساده سری RLC زیر را در نظر بگیرید.
مدار سری RLC
ابتدا، اجازه دهید، آنچه را که تا الان در مورد مدارهای سری RLC، میدانیم مرور کنیم.
راکتانس القایی
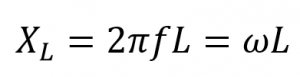
راکتانس خازنی
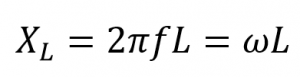
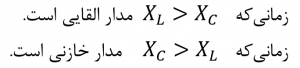
راکتانس کلی مدار
امپدانس کلی مدار
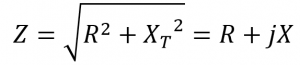
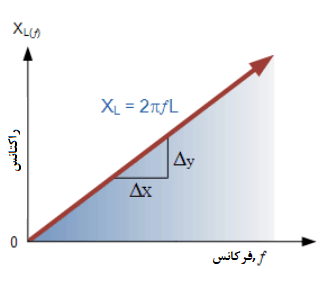
با توجه به معادله بالا برای راکتانس القایی، اگر فرکانس یا اندوکتانس افزایش یابد؛ مقدار کل راکتانس القایی سلف؛ نیز افزایش مییابد. با میلکردن فرکانس به بینهایت؛ راکتانس سلفها نیز به سمت بینهایت میل کرده و عنصرمدار، مانند یک مدارباز عمل میکند.
با اینحال، با نزدیکشدن فرکانس به صفر یا DC، راکتانس سلفها به سمت صفر کاهش یافته و باعث اثر معکوس شده و مانند یک اتصال کوتاه عمل میکند. این بدان معنی است، که راکتانس القایی “متناسب” با فرکانس است و در فرکانسهای کم، مقدار کم و در فرکانسهای بالا، مقدار زیاد دارد. این منحنی در زیر نشان داده شدهاست:
راکتانس القایی درمقابل فرکانس
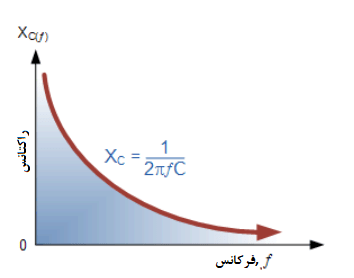
نمودار راکتانس القایی، در برابر فرکانس، یک منحنی خطی مستقیم است. مقدار راکتانس القایی با افزایش فرکانس، افزایش مییابد. از اینرو، راکتانس القایی، مثبت بوده و به صورت مستقیم متناسب با فرکانس است (XL α f). این مورد، برای فرمول راکتانس خازنی بالا نیز، بهصورت معکوس، صادق است. اگر فرکانس یا ظرفیت افزایش یابد؛ راکتانس کلی خازنی کاهش مییابد. با نزدیکشدن فرکانس به بینهایت، راکتانس خازنها تقریبا به صفر رسیده و باعث میشود، عنصر مدار مانند یک رسانای کامل 0Ω عمل کند.
اما با نزدیکشدن فرکانس به صفر یا DC، راکتانس خازنها بهسرعت تا بینهایت افزایش یافته و باعث میشود مانند یک مقاومت بسیار بزرگ عمل کرده و بیشتر بهصورت مدارباز عمل میکند؛ این بدین معنی است، که راکتانس خازنی، برای هر مقدار دادهشده خازن “نسبت معکوس“ با فرکانس دارد؛ که در زیر نشان داده شده است.
راکتانس خازنی درمقابل فرکانس
نمودار راکتانس خازنی در برابر فرکانس، یک منخنی هایپربولیک است. مقدار راکتانس یک خازن، در فرکانسهای پایین، مقدار بسیار بالایی دارد؛ اما با افزایش فرکانس به سرعت کاهش مییابد. بنابراین، راکتانس خازنی، مقدار منفی داشته و با فرکانس، نسبت معکوس دارد(XC α f-1).
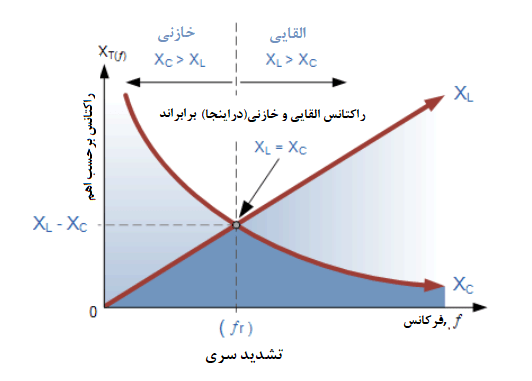
میتوانیم ببینیم، که مقادیر این مقاومتها به فرکانس منبع تغذیه وابسته است. در فرکانسهای بالاتر، مقدار XL زیاد بوده؛ در حالیکه در فرکانس پایین، مقدار XC زیاد میشود. اگر ، منحنی راکتانس القایی را در بالای منحنی راکتانس خازنی قرار دهیم تا هر دو منحنی در محورهای یکسانی قرار بگیرند؛ نقطه برخورد، نقطهی فرکانس تشدید سری ( ƒr یا ωr) را به ما نشان میدهد که در زیر آمدهاست.
فرکانس تشدید سری
درجاییکه که fr برحسب هرتز، L برحسب هنری و C برحسب فاراد است.
تشدید الکتریکی در مدار AC، زمانی اتفاق میافتد؛ که تاثیرات دو راکتانس که برابر اما در مخالف میباشند، یکدیگر را بهصورت XL=XC خنثی کنند. نقطهای که در نمودار بالا نشان دادهشد؛ نقطهای است؛ که در آن، این اتفاق میافتد، جایی است که دو نمودار از کنار یکدیگر عبور میکنند. در یک مدار تشدید سری، نقطه فرکانس تشدید (fr) را میتوان بهصورت زیر محاسبه کرد:
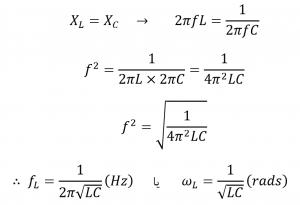
میتوانیم بگوییم که در تشدید، از نظر ریاضی دو راکتانس، یکدیگر را بهصورت XL – XC = 0 خنثی میکنند. این باعث میشود؛ ترکیب سری LC، بهصورت اتصال کوتاه عمل کرده و تنها مقدار مخالفت با جریان جاری در مدار تشدید سری، مقاومت R باشد.
در فرم مختلط، فرکانس تشدید، فرکانسی است؛ که در آن امپدانس کلی مدار سری RLC، کاملا حقیقی بوده و هیچ امپدانس مختلطی درآن وجود ندارد؛ به این دلیل که در تشدید خنثی شدهاست. درنتیجه، امپدانس کلی مدار سری تنها برابر با مقدار مقاومت بوده و درنتیجه : Z=R است.
پس در تشدید، امپدانس مدار سری، دارای بیشترین مقدار خود بوده و برابر با مقاومت R مدار است. امپدانس مدار در تشدید را ،”امپدانس دینامیک” مدار میگویند که وابسته به فرکانس (XC به طور معمول در فرکانسهای بالا یا XL به طورمعمول در فرکانسهای پایین) بوده که بر هردوطرف تشدید مسلط است؛ که در زیر نشان داده شدهاست.
امپدانس در مدار تشدید سری
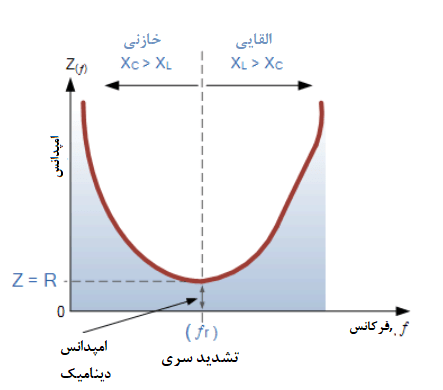
توجه داشتهباشید که؛ وقتی راکتانس خازنی بر مدار غلبه میکند؛ منحنی امپدانس برای خود شکل هایپربولیک دارد؛ اما هنگامیکه، راکتانس القایی بر مدار مسلط شود، منحنی بهدلیل پاسخ خطی XL، غیرمتقارن خواهد بود.
ممکن است به این نیز توجه کرده باشید؛ که اگر امپدانس مدار، دارای حداقل مقدار خود در تشدید باشد؛ درنتیجه، ادمیتانس مدار باید دارای حداکثر مقدار خود باشد و یکی از مشخصات تشدید سری، ادمیتانس بسیار بالا میباشد. اما این میتواند اتفاق بدی باشد؛ زیرا مقدار بسیار کم مقاومت در برابر تشدید، به این معناست؛ که جریان جاری در مدار، در حد خطرناکی، زیاد است.
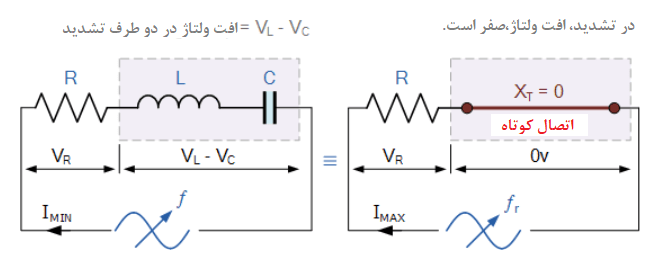
از مقاله قبلی در مورد مدارهای سری RLC، به یاد میآوریم؛ که ولتاژ در یک ترکیب سری، مجموع فازوری VR ، VLو VC است. پس، اگر در تشدید دو راکتانس برابر و خنثیکننده باشند، دو ولتاژ ، VLو VC دارای مقدار مثبت و برابر از نظر اندازه بوده و بدین ترتیب، بهدلیل اینکه مولفههای خالص ولتاژهای فازور به ترتیب در °90+ و °90- رسم میشوند، یکدیگر را خنثی میکنند.
در یک مدار تشدید سری، ولتاژهای راکتیو حاصل صفر میباشند ( VL=-VC ) و کل افت ولتاژ منبع تغذیه بر روی مقاومت خواهد بود. بنابراین VR=VSupply بوده و به همین دلیل است که مدارهای تشدید سری به عنوان مدارهای تشدید ولتاژ شناخته میشوند(در مقابل مدارهای تشدید موازی، مدارهای تشدید جریان میباشند.)
مدار سری RLC در حال تشدید
ازآنجاییکه، جریان عبوری از یک مدار تشدید سری، حاصل تقسیم ولتاژ بر امپدانس (Z) است؛ و در کمترین مقدار خود (=R) است. از اینرو، جریان جاری در این فرکانس، حداکثر مقدار V/R بوده که در زیر آمده است:
جریان مدار سری در حال تشدید
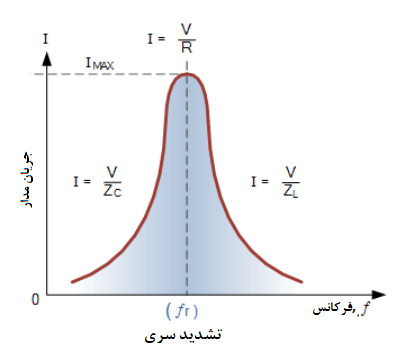
منحنی پاسخ فرکانسی مدار تشدید سری، نشان میدهد؛ که مقدار جریان تابعی از فرکانس است و رسم آن روی نمودار به ما نشان میدهد که پاسخ از نزدیکی صفر شروع شده، در فرکانس تشدید به حداکثر مقدار خود، زمانیکه IMAX = IR است، رسیده و سپس تا نزدیکی صفر، زمانیکه f، بینهایت میشود، میرود. نتیجه این عمل، این است؛ که اندازه ولتاژ دو سر سلف L و خازن C، بسیار بزرگتر از ولتاژ منبع تغذیه،گشته حتی در هنگام تشدید؛ اما این مقدار برابر و در مخالف با یکدیگر بوده که یکدیگر را خنثی میکنند.
از آنجایی که، مدار تشدید سری، تنها بر روی فرکانس تشدید کار میکند؛ این نوع مدار، بهعنوان مدار پذیرنده نیز شناخته میشود. زیرا در تشدید، امپدانس مدار در کمترین حد خود است. بنابراین، جریانی را که فرکانس آن، برابر با فرکانس تشدید آن است، بهراحتی قبول میکند.
همچنین ممکن است متوجه شده باشید؛ که چون حداکثر جریان جاری در مدار تشدید، فقط با مقدار مقاومت (مقدار خالص و حقیقی) محدود میشود؛ بنابراین ولتاژ منبع تغذیه و جریان مدار، باید در این فرکانس با یکدیگر هم فاز باشند. پس زاویهفاز بین ولتاژ و جریان یک مدار تشدید سری، نیز تابعی از فرکانس برای یک ولتاژ تغذیه ثابت بوده و در نقطه فرکانس تشدید، صفر است؛ زمانیکه V، I و VR، همه همفاز با یکدیگر میباشند که در شکل زیر آمدهاست. درنتیجه، اگر زاویهفاز صفر باشد؛ بنابراین ضریب توان باید برابر با 1 باشد.
زاویه فاز مدار تشدید سری
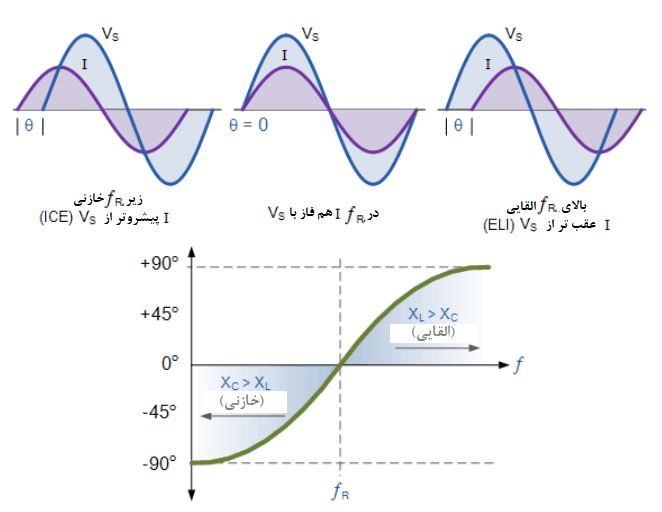
همچنین توجه داشتهباشید؛ که زاویهفاز برای فرکانسهای بالای fr، مثبت بوده و زاویهفاز برای فرکانسهای زیر fr، منفی است که با فرمول زیر اثبات میشود.
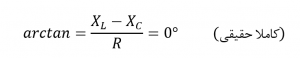
پهنای باند مدار تشدید سری
اگر مدار سری RLC، توسط یک فرکانس متغیر برای یک ولتاژ ثابت هدایت شود؛ اندازه جریان I متناسب با امپدانس Z بوده و درنتیجه، در تشدید، توان جذبشده توسط مدار باید حداکثر مقدار خود را که معادل P = I2Z است؛ داشته باشد.
اگر ما فرکانس را تا نصف حداکثر توان متوسط جذبشده توسط مقاومت در تشدید، در مدار تشدید سری، کاهش یا افزایش دهیم؛ دو نقطهی فرکانسی به نام نقاط نصف توان تولید خواهد شد؛ که اگر 0dB بهعنوان حداکثر جریان مرجع در نظر گرفته شود؛ این نقاط 3dB- زیر حداکثر خواهند بود.
این نقاط 3dB- ، به ما مقدار جریانی برابر 70.7% حداکثر مقدار تشدید را خواهند داد؛ که بهصورت 0.5 ( I2 R ) = (0.707 x I) 2 R تعریف میشوند. سپس نقطه مربوط به فرکانس پایین در نصف توان را “فرکانسقطع پایین” مینامند، که با fL شناخته میشود و نقطه مربوط به فرکانس بالا در نصف توان، “فرکانسقطع بالا” است، که fH نماد آن است. فاصله بین این دو نقطه، درنتیجه، (fH-fL) بوده که پهنای باند (BW) نام دارد و محدودهای از فرکانسهاست که حداقل، نصف توان حداکثر و جریان در آن تامین شده است. در زیر داریم:
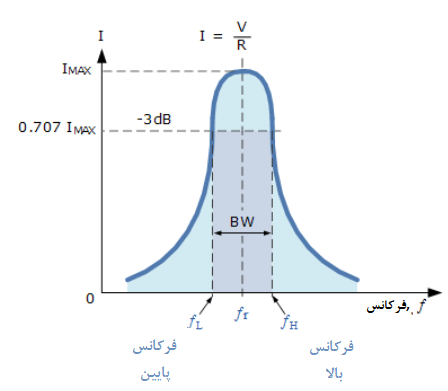
پاسخ فرکانسی اندازه جریان مدارها در بالا، به “sharpness” تشدید در مدار تشدید سری وابسته است. شارپنس پیک از لحاظ کمی اندازهگیری شده و ضریب کیفیت (Q) مدار نامیده میشود. ضریب کیفیت، نسبت حداکثر یا انرژی پیک ذخیرهشده در مدار (راکتانس) به انرژی تلفشده (مقاومت) در طی هر سیکل نوسان است؛ به این معنا که این نسبت، نسبت فرکانس تشدید به پهنایباند است و هرچه Q مدار بیشتر باشد، پهنایباند کوچکتر است (Q = ƒr /BW).
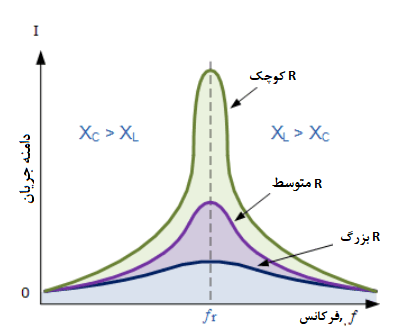
ازآنجاییکه، پهنایباند، جایی در میان دو نقطه 3dB- میباشد؛ انتخابپذیری (selectivity) مدار، اندازهگیری توانایی آن در رد هر فرکانس، در هردو طرف این نقاط است. یک مدار با انتخابپذیری بیشتر دارای پهنایباند باریکتر بوده؛ درحالیکه یک مدار با انتخابپذیری کمتر دارای پهنایباند وسیعتری خواهد بود. انتخابپذیری یک مدار تشدید سری را، میتوان تنها با تنظیم مقدار مقاومت و نگهداشتن بقیه عناصر بدون تغییر، کنترل نمود.
از آنجایی که Q = (XL or XC) / R خواهد بود.
پهنای باند مدار تشدید سری RLC
رابطهی بین تشدید، پهنایباند، انتخابپذیری و ضریب کیفیت یک مدار تشدید سری بهصورت زیر است:
فرکانس تشدید ( ƒr )
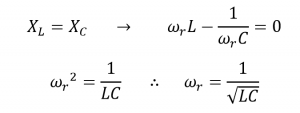
جریان ( I )
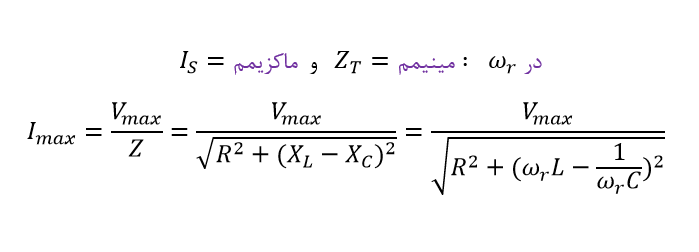
فرکانس قطع پایین ( ƒL )
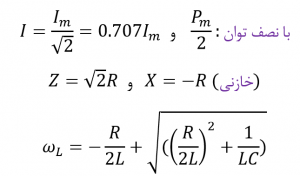
فرکانس قطع بالا ( ƒH )
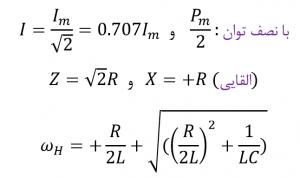
پهنای باند ( BW )
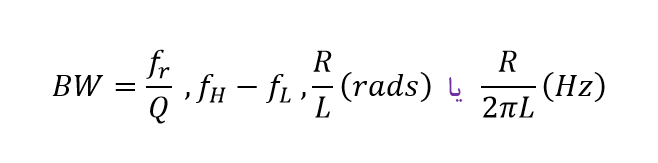
ضریب کیفیت ( Q )
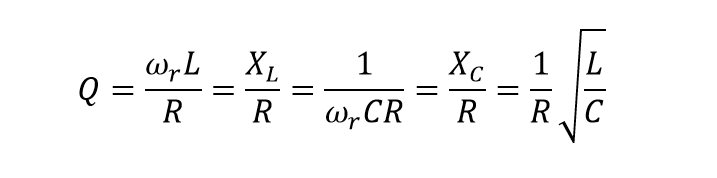
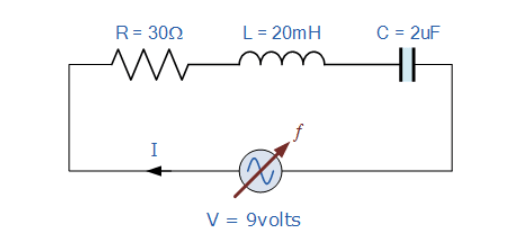
مثال شماره 1- تشدید سری
یک شبکهی تشدید سری، متشکل از یک مقاومت 30Ω، یک خازن 2uF و یک سلف 20mH به یک ولتاژ منبع تغذیه سینوسی متصل است؛ که دارای خروجی ثابت 9 ولت برای همه فرکانسهاست. فرکانس تشدید، جریان هنگام تشدید، ولتاژ دوسر سلف و خازن هنگام تشدید، ضریب کیفیت و پهنایباند را محاسبه کنید. همچنین شکلموج جریان مربوطه را برای همه فرکانسها ترسیم کنید.
فرکانس تشدید ( ƒr )
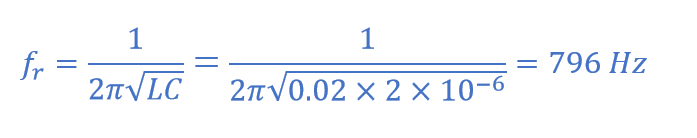
جریان مدار هنگام تشدید ( Im )
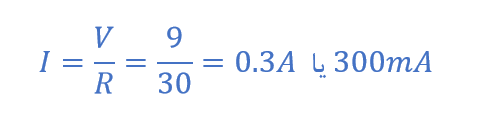
راکتانس القایی هنگام تشدید ( XL )
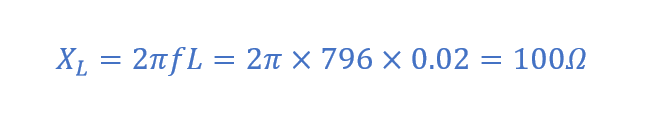
ولتاژهای دو سر سلف و خازن ( VL, VC )
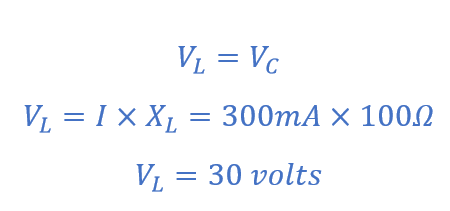
توجه: ولتاژ تغذیه، ممکن است؛ فقط 9 ولت باشد، اما هنگام تشدید، ولتاژهای راکتیو دو سر خازن (VC) و سلف (VL)، 30 ولت پیک میباشند.
ضریب کیفیت (Q)
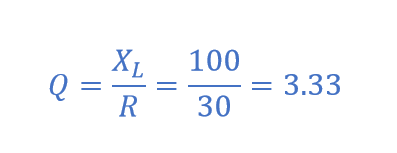
پهنای باند ( BW)
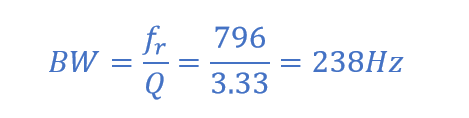
نقاط فرکانس پایین و بالای 3dB – (ƒH و ƒL)
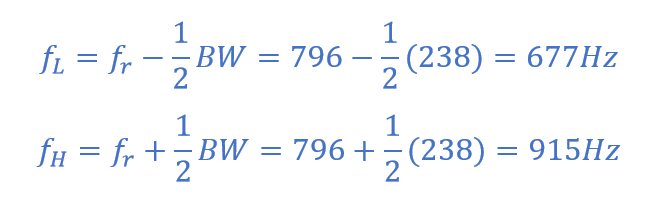
شکل موج جریان
مثال شماره 2 - تشدید سری
یک مدار سری متشکل از، یک مقاومت 4Ω، یک سلف 500mH و یک خازن متغیر، به یک منبعتغذیه 100V,50Hz متصلشدهاست. ظرفیت موردنیاز برای تولید یک وضعیت تشدید سری و ولتاژهای تولیدشده در دوسر سلف و خازن در نقطه تشدید را محاسبه کنید.
فرکانس تشدید ( ƒr )
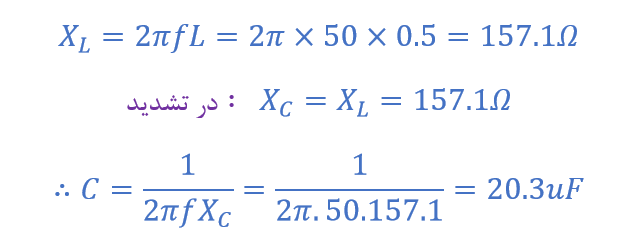
ولتاژهای دو سر سلف و خازن ( VL, VC )

خلاصه تشدید سری
هنگام تجزیه و تحلیل مدارهای تشدید سری در این مقاله، ما به پهنایباند، نقاط3dB – فرکانسهای قطع بالا و پایین، ضریب Q یا کیفیت پرداختیم. همه این موارد، اصطلاحاتی میباشند که در طراحی و ساختن فیلترهای میانگذر (BPF) استفاده میگردند و در واقع، مدارهای تشدیدی در طراحی فیلترهای سه عنصری استفاده میشوند تا تمام فرکانسها در محدوده “باندعبور” را عبورداده؛ در حالیکه بقیه را رد میکنند.
با اینحال، هدف اصلی این آموزش، تجزیه و تحلیل و درک مفهوم تشدید سری در مدارهای پسیو سری RLC بوده و طراحی فیلترهای RLC خارج از محدوده این آموزش خاص است و متاسفانه در اینجا بررسی نمیگردد.
- برای رخدادن تشدید در هرمداری، مدار باید حداقل دارای یک سلف و یک خازن باشد.
- تشدید، نتیجه نوسانات در مدار؛ در هنگامیاست که انرژی ذخیرهشده از سلف به خازن منتقل میگردد.
- تشدید، در زمانی رخ میدهد؛ که XL = XC است و بخش موهومی این تابع انتقال صفر است.
- در تشدید، امپدانس مدار برابر با مقدار مقاومت، یعنی Z = R است.
- در فرکانسهای پایین، مدار سری خازنی بوده، چون XC > XL است که به مدار ضریب توان پیشرو میدهد.
- در فرکانسهای بالا، مدار سری القایی بوده، چون XL > XC است که به مدار ضریب توان عقبمانده میدهد.
- مقدار جریان بالا در تشدید، مقادیر بالایی از ولتاژ دوسر سلف و خازن را تولید میکند.
- مدارهای تشدید سری برای ساخت فیلترهای با فرکانس بالای انتخابپذیر، مفید است.
- درهرحال، مقدار بالای جریان و مقادیر بالای ولتاژ عناصر مدار، میتواند سبب آسیب به مدار گردد.
- برجستهترین ویژگی پاسخ فرکانسی یک مدار تشدیدی، پیک تیز تشدید در مشخصات دامنه است.
- بهدلیل امپدانس حداقل و جریان حداکثر، به مدارهای سری تشدید، مدارهای پذیرنده نیز میگویند.
در مقاله بعدی، در مورد تشدید موازی، به بررسی چگونگی تاثیر فرکانس بر خصوصیات یک مدار موازی RLC و اینکه چگونه ضریب Q در یک مدار تشدید موازی، بر بزرگنمایی جریان اثرگذار است؛ خواهیم پرداخت .







2 دیدگاه در “مدار تشدید سری”
دم شما گرم
درود دوستان
در بحث فرکانس تشدید سری، وقتی از یک طرف معادله جذر گرفته میشود ، طرف اول باید f قید شود نه f به توان ۲
همچنین fl برای فرکانس رزونانس در قدیم استفاده میشد ، در حال حاضر Fr مینویسند
متشکرم از مقاله خوبتون