27 مهر 1400

جمع کننده ی باینری

بازدید: 2302

27 مهر 1400

جمع کننده ی باینری

بازدید: 2302

جمع‌کننده‌های باینری، مدارهای حسابی، به شکل نیم‌جمع‌کننده‌ها و جمع‌کننده‌های کامل می‌باشند؛ که برای جمع‌کردن دو رقم باینری با یک‌دیگر، استفاده می‌شوند.

یکی دیگر از مدارهای منطقی ترکیبی رایج و بسیار مفیدی، که تنها با استفاده از چند گیت منطقی اساسی، ایجاد می‌شود و امکان جمع دو یا چند عدد باینری را فراهم می‌کند؛ جمع‌کننده‌ی باینری نام دارد.

یک مدار جمع‌کننده‌ی باینری پایه، می‌تواند از گیت‌های استاندارد AND و Ex-OR ساخته شود؛ تا دو عدد تک بیت باینری A و B را بتوان با یک‌دیگر، “جمع” نمود.

افزودن این دو رقم به یک‌دیگر، براساس قوانین جمع باینری، یک خروجی به ‌نام SUM(مجموع) و یک خروجی دوم به ‌نام CARRY یا Carry-out(Cout) به معنای رقم نقلی، تولید می‌کند. یکی از استفاده‌های اصلی جمع‌کننده‌ی باینری، در محاسبات و شمارش مدارات است. جمع ساده‌ی دو عدد ده‌دهی(مبنای 10) زیر را در نظر بگیرید.

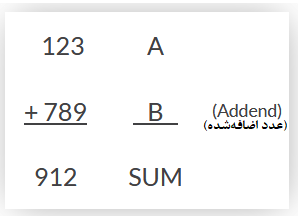
از درس‌های ریاضی در مدرسه، متوجه شدیم؛ که هر ستون عدد، از سمت راست باهم جمع می‌شوند و هر رقم، بسته به موقعیت خود در ستون، دارای مقدار وزنی(یکان، دهگان، صدگان و…) است. هنگامی‌که، هر ستون به‌ دیگری اضافه می‌شود؛ اگر نتیجه بزرگتر یا مساوی 10 باشد؛ یک رقم نقلی، تولید می‌شود. سپس، این رقم نقلی، به نتیجه‌ی مجموع ستون سمت چپ بعدی، اضافه می‌شود و اینگونه ادامه می‌یابد. این عمل، یک عملیات جمع ساده‌ی مدرسه است؛ که ابتدا اعداد و بعد رقم نقلی‌ها به هم اضافه می‌گردند.

افزودن اعداد باینری، دارای همان ایده‌ی جمع اعداد ده‌دهی به یک‌دیگر است؛ با این تفاوت، که این بار رقم نقلی، زمانی تولید می‌شود؛ که هر ستون، بزرگتر یا برابر با “2” شود؛ که مبنای عدد باینری است. به بیان‌دیگر، 1+1 سبب تولید رقم نقلی می‌شود.

جمع باینری

جمع باینری، از همان قوانین اساسی برای جمع ده‌دهی پیروی می‌کند؛ اما در سیستم باینری، تنها دو رقم وجود دارد و بزرگترین رقم “1” است. بنابراین، هنگام افزودن اعداد باینری، خروجی نقلی، زمانی تولید می‌شود؛ که “مجموع (SUM)” برابر یا بزرگتر از دو (1+1) باشد و این، یک بیت “نقلی (CARRY)” برای هرگونه افزودنی، برای افزودن و انتقال به ستون بعدی است و اینگونه، ادامه می‌یابد. جمع یک بیت واحد، در زیر را درنظر بگیرید:

مجموع باینری دو بیت

زمانی‌که، دو بیت واحد A و B، به یک‌دیگر، اضافه می‌گردند؛ جمع “0+0″، “1+0” و “0+1” منجر به “0” یا “1” می‌شود؛ تا زمانی‌که، ستون نهایی برابربا “1+1” شود و یعنی مجموع برابر با “2” گردد. اما عدد دو در باینری وجود ندارد و معادل آن در باینری، برابر با 10 است. به بیان دیگر، یک صفر برای مجموع، به‌علاوه‌ی یک بیت نقلی اضافی، خواهیم داشت.

د نتیجه، عملکرد یک جمع‌کننده‌ی ساده، نیاز به دو ورودی داده دارد؛ که دو خروجی تولید می‌کند. جمع(S)معادله و بیت نقلی(C)، به‌صورت زیر است:

بلوک دیاگرام جمع‌کننده‌ی باینری

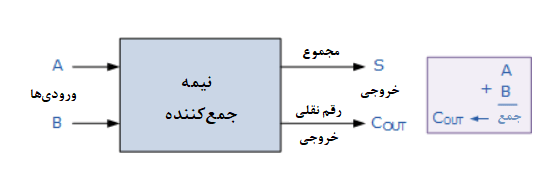
برای مسئله‌ی جمع یک بیتی ساده‌ی بالا، بیت نقلی حاصل، می‌تواند نادیده گرفته‌شود. اما ممکن است؛ درمورد افزودن این دوبیت، چیز دیگری را متوجه شده‌باشید. مجموع باینری بالا، شبیه به یک گیت انحصاری OR(Exclusive OR) است. اگر دو بیت را به‌عنوان A و B، برچسب‌گذاری کنیم؛ جدول درستی حاصل، مجموع دو بیت بدون رقم نقلی نهایی است.

گیت دو ورودی Ex-OR

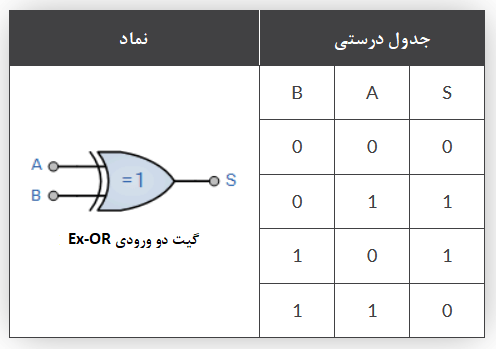
از جدول درستی بالا، می‌توانیم ببینیم؛ که گیت انحصاری OR، فقط زمانی خروجی “1” تولید می‌کند؛ که یکی از ورودی‌ها در منطق “1” باشد. اما زمانی‌که، هر دو “1” باشند؛ این اتفاق نمی‌افتد؛ درحالی‌که برای مجموع باینری دو بیت قبلی، اتفاق می‌افتاد. با این‌حال، برای انجام جمع دو عدد، ریزپردازنده‌ها و ماشین‌حساب‌های الکترونیکی، نیاز به بیت نقلی اضافی، برای محاسبه‌ی صحیح معادلات دارند و بنابراین، باید جمع‌بندی قبلی را بازنویسی کنیم؛ تا شامل دو بیت داده خروجی، مانند تصویر زیر باشد.

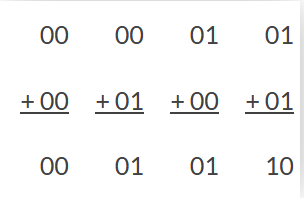
از معادلات فوق، می‌دانیم که یک گیت انحصاری OR، تنها زمانی ورودی “1” تولید می‌کند؛ که “یکی” از دو ورودی در منطق “1” باشد و ازاین‌رو، به یک خروجی اضافی برای تولید بیت نقلی، وقتی‌که، هردو ورودی A و B، در منطق “1” هستند؛ نیاز است. یک گیت دیجیتال که کاملا منطبق با این نیاز است و سبب تولید خروجی “1”، درصورت برابربودن هردو ورودی A و B با “1”(HIGH) می‌شود؛ گیت استاندارد AND است.

گیت دو ورودی AND

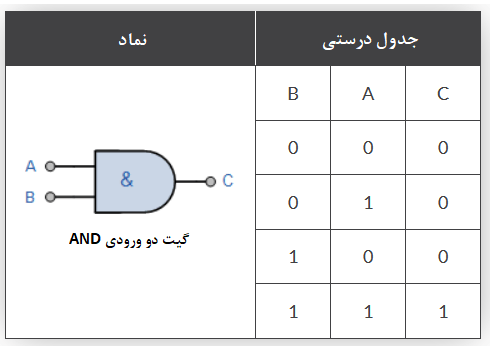
با ترکیب گیت انحصاری OR با گیت AND، یک مدار جمع‌کننده‌ی باینری ساده‌ی دیجیتال خواهیم داشت؛ که معمولا مدار “نیم جمع‌کننده“، نامیده می‌شود.

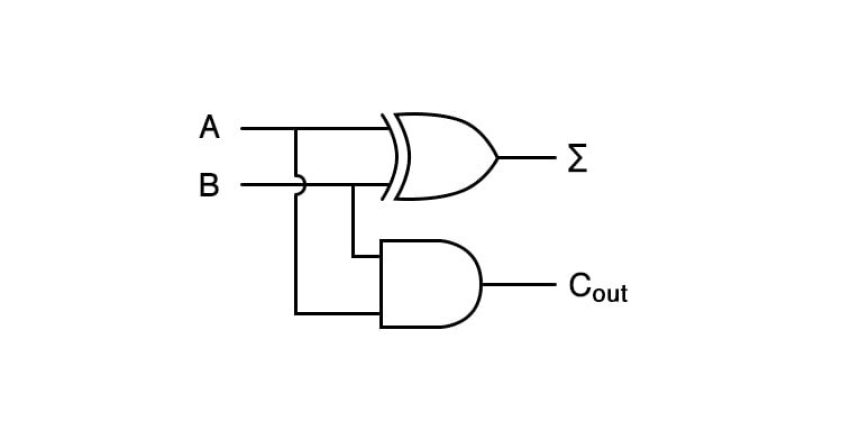
یک مدار نیم جمع‌کننده

یک نیم جمع‌کننده، یک مدار منطقی است؛ که عمل جمع را برروی دو رقم باینری، انجام می‌دهد. این نیم جمع‌کننده، یک مجموع و یک مقدار نقلی، که هردو رقم باینری می‌باشند؛ تولید می‌کند.

جدول درستی یک نیمه جمع‌کننده با خروجی نقلی

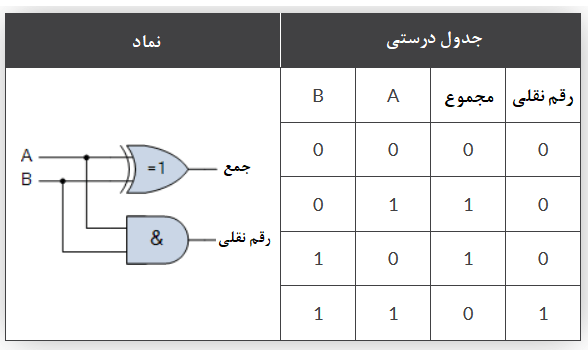
از جدول درستی بالا برای نیم جمع‌کننده، می‌توانیم ببینیم که خروجی مجموع (S) نتیجه‌ی گیت انحصاری OR و خروجی نقلی (Cout) نتیجه‌ی گیت AND است. پس عبارت بولین برای یک نیم جمع‌کننده، به‌صورت زیر است:

برای بیت مجموع:

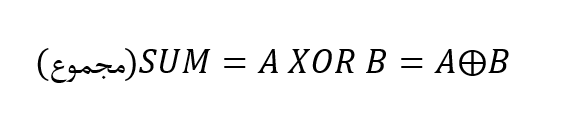
برای بیت نقلی:

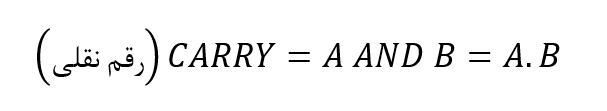
یکی از معایب اصلی مدار نیم جمع‌کننده، زمانی‌که به‌عنوان جمع‌کننده‌ی باینری به‌کار می‌رود؛ این است؛ که هنگام جمع چند بیت داده با یک‌دیگر، هیچ پیش‌بینی برای “رقم نقلی ورودی(Carry-in)” از مدار قبلی، وجود ندارد.

برای مثال، فرض کنید ما می‌خواهیم؛ دو بایت داده‌ی 8 بیتی را، باهم جمع کنیم. هر بیت نقلی حاصل، باید بتواند از طریق کم ارزش‌ترین بیت(LSB) “موج‌دار” شود یا در الگوهای بیت، حرکت کند. پیچیده‌ترین عملی که یک نیم جمع‌کننده، می‌تواند انجام دهد، “1+1” است. اما به‌دلیل نداشتن ورودی نقلی، مقدار جمع‌شده‌ی نهایی، نادرست خواهدشد. یک راه ساده برای غلبه بر این مشکل، استفاده از نوع جمع‌کننده‌ی کامل مدار جمع‌کننده‌ی باینری است.

یک مدار جمع‌کننده کامل

تفاوت اصلی بین جمع‌کننده‌ی کامل و نیم‌ جمع‌کننده‌ی پیشین، این است؛ که جمع‌کننده‌ی کامل، دارای سه ورودی می‌باشد. دو ورودی‌ داده‌ی تک بیتی A و B، همانند قبل، به‌علاوه‌ی یک ورودی نقلی(C-in) اضافی که بتواند رقم نقلی را از مرحله‌ی قبلی، دریافت کند؛ که در زیر نشان داده شده‌است.

بلوک دیاگرام جمع‌کننده کامل

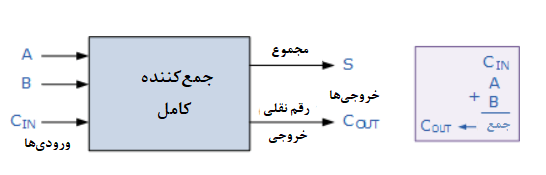
پس یک جمع‌کننده‌ی کامل، یک مدار منطقی است؛ که عملیات جمع را برروی سه رقم باینری اجرا می‌کند و همانند نیم‌ جمع‌کننده، یک رقم نقلی خروجی برای ستون جمع بعدی، تولید می‌نماید. پس یک ورودی نقلی(Carry-in)، یک رقم نقلی احتمالی از یک رقم با ارزش پایین‌تر است؛ درحالی‌که، خروجی نقلی(Carry-out)، نشان‌دهنده‌ی رقم نقلی با ارزش بیشتر است. از بسیاری از جهات، می‌توان یک جمع‌کننده‌ی کامل را، دو نیم جمع‌کننده که به یک‌دیگر اتصال یافته‌اند؛ فرض نمود. درحالی‌که، نیم جمع‌کننده‌ی اول، رقم نقلی خود را به نیم جمع‌کننده‌ی دوم، انتقال می‌دهد.

بلوک دیاگرام جمع‌کننده کامل

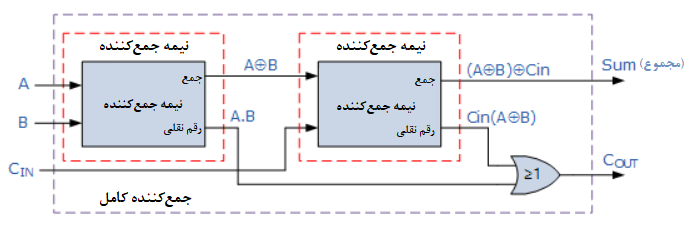
از آنجایی‌که، مدار جمع‌کننده‌ی کامل در بالا، اساسا دو نیم جمع‌کننده‌ی اتصال یافته به یک‌دیگر است؛ جدول درستی برای جمع‌کننده‌ی کامل، شامل یک ستون اضافی برای درنظرگرفتن ورودی نقلی(Carry-in(C_IN)) به‌ همراه بیت خروجی جمع(S) و بیت خروجی نقلی(Carry-out(C_out)) است.

جدول درستی جمع‌کننده کامل با رقم نقلی

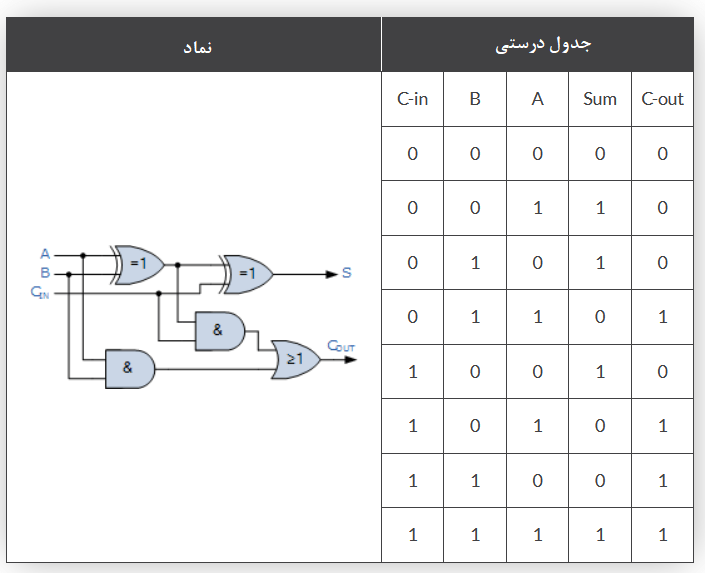
بنابراین، عبارت بولین برای جمع‌کننده‌ی کامل به‌صورت زیر است:

برای بیت مجموع(S):

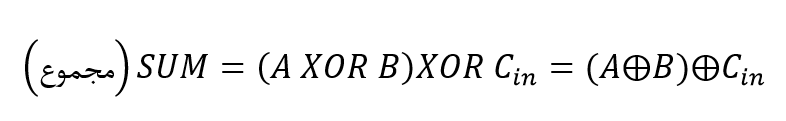
برای بیت نقلی (Cout):

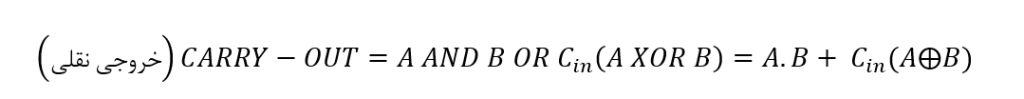
یک جمع‌کننده باینری n بیت

در بالا دیدیم؛ که جمع‌کننده‌های تک بیتی باینری، می‌توانند از گیت‌های منطقی پایه، ساخته‌شوند. اما اگر بخواهیم دو عدد n بیتی را با یک‌دیگر جمع کنیم؛ چه باید کرد؟! بنابراین، n عدد جمع‌کننده‌ی کامل تک بیتی، نیاز داریم تا به یکدیگر متصل یا “کسکید” شوند و بتوان آنچه به‌عنوان جمع‌کننده‌ی نقلی موج‌دار شناخته می‌شود؛ تولیدکرد.

یک جمع‌کننده‌ی نقلی موج‌دار، به‌سادگی تعداد n جمع‌کننده‌ی کامل تک بیتی کسکیدشده به یکدیگر است؛ که هر جمع‌کننده‌ی کامل، نشان‌دهنده‌ی یک ستون وزن‌دار واحد، در یک جمع باینری طولانی است. به آن جمع‌کننده‌ی نقلی موج‌دار می‌گویند؛ زیرا سیگنال‌های نقلی آن، یک اثر “موج” در جمع‌کننده‌ی باینری، از راست به چپ(LSB به MSB) ایجاد می‌کنند.

برای مثال، فرض کنید؛ می‌خواهیم دو عدد 4 بیتی را با یکدیگر، “جمع” کنیم؛ دو خروجی جمع‌کننده‌ی کامل اول، موقعیت مجموع رقم اول(S) از مجموع را به‌علاوه‌ی بیت خروجی نقلی فراهم می‌کند؛ که به‌عنوان رقم ورودی نقلی برای جمع‌کننده‌ی باینری بعدی، عمل می‌کند.

جمع‌کننده‌ی باینری دوم در زنجیر نیز، یک خروجی جمع‌شده( بیت دوم) به‌علاوه‌ی بیت خروجی نقلی دیگری، تولید می‌کند و درنتیجه، ما می‌توانیم جمع در جمع‌کننده‌ی کامل را ادامه دهیم تا ترکیبی از جمع اعداد بزرگتر را، با متصل‌کردن بیت خروجی نقلی از جمع‌کننده‌ی کامل باینری اول به جمع‌کننده‌ی کامل بعدی، بسازیم و ادامه دهیم. یک مثال از یک جمع‌کننده‌ی 4 بیتی، در زیر آورده شده‌است.

یک جمع‌کننده 4 بیتی رقم نقلی موج‌دار

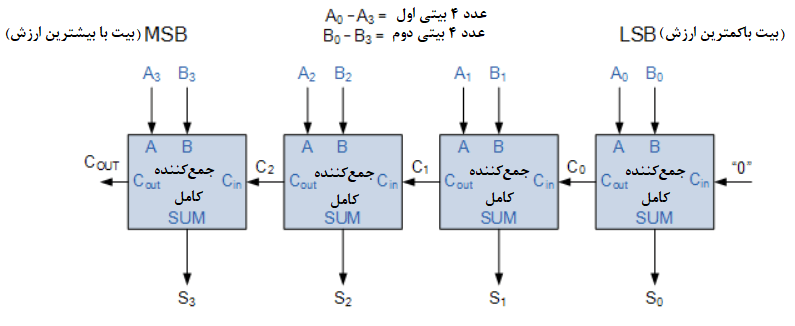
یکی از معایب اصلی “کسکیدکردن” جمع‌کننده‌های باینری تک بیتی به یک‌دیگر، برای جمع اعداد باینری بزرگتر، این است؛ که اگر ورودی‌های A و B، تغییریابند؛ مجموع در خروجی آن، تا زمانی‌که هر ورودی نقلی، در زنجیره‌ی هر جمع‌کننده‌ی کامل “موج‌دار” شود؛ معتبر نخواهد بود. زیرا با ارزش‌ترین بیت(MSB) جمع، باید برای هر تغییری از ورودی نقلی کم ارزش‌ترین بیت(LSB)، صبرکند. درنتیجه، قبل از اینکه خروجی جمع‌کننده، به هر تغییری در ورودی‌های آن و درنتیجه تاخیر انباشته، پاسخ دهد؛ تاخیر محدودی خواهد داشت.

در صورت زیادنبودن اندازه بیت‌های اضافه‌شده، برای مثال 4 بیت یا 8 بیت، یا مهم‌نبودن سرعت جمعِ جمع‌کننده‌، ممکن است؛ این تاخیر، بدون اهمیت باشد. با این‌حال، زمانی‌که اندازه‌ی بیت‌ها بزرگتر باشد؛ برای مثال 32 یا 64 بیت در جمع‌کننده‌های چندبیتی، استفاده شود یا جمع‌بندی با سرعت کلاک(ساعت) بسیار بالا، موردنیاز باشد؛ این تاخیر ممکن است؛ به‌طرز غیرقابل تحملی، بزرگ شود. زیرا فرآیند جمع، به‌درستی درون یک سیکل ساعت، کامل نشده‌است.

این زمان تاخیر ناخواسته را، تاخیر انتشار می‌نامند. هم‌چنین، مشکل دیگری به‌نام “سرریز شدن”، هنگامی‌ که یک جمع‌کننده‌ی n بیتی، دو عدد موازی را باهم جمع می‌کند؛ که مجموع آن‌ها بزرگتر یا مساوی 2ⁿ است؛ رخ می‌دهد.

یک راه، تولید سیگنال‌های ورودی نقلی، مستقیما از ورودی‌های A و B، به‌جای استفاده از چیدمان موج‌دار بالا، است. سپس، این عمل، نوع دیگری از مدار جمع‌کننده‌ی باینری را، که جمع‌کننده‌ی باینری نقلی نگاه به جلو(Carry Look Ahead Binary Adder) نامیده می‌شود؛ درجایی‌که سرعت جمع‌کننده‌ی موازی، می‌تواند با استفاده از منطق نقلی نگاه به جلو، به‌طرز شدیدی ارتقا یابد؛ تولید می‌کند.

مزیت این جمع‌کننده‌ها، این است؛ که مدت زمان لازم برای تولید جمع صحیح، مستقل از تعداد بیت‌های مورد استفاده در عملیات است. و این امر، خلاف چرخه‌ی زمانی یک جمع‌کننده‌ی موج‌دار موازی است؛ که نیاز به کامل‌کردن مجموع دارد؛ که توسط عملیات جمع تعداد کل بیت‌ها، انجام می‌گیرد.

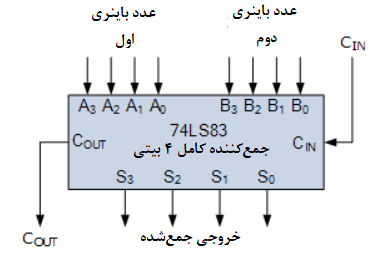
مدارهای جمع‌کننده‌ی کامل 4 بیتی با مشخصه‌های نقلی نگاه به‌جلو، به‌عنوان پکیج‌های IC استاندارد، جمع‌کننده‌ی باینری 4 بیتی TTL،74LS83 یا 74LS283 و CMOS 4008 وجود دارند؛ که به‌صورت دو عدد باینری 4 بیتی، باهم جمع شده‌اند و یک خروجی جمع و رقم نقلی، به‌صورت زیر تولید می‌کنند.

نماد منطقی 74LS83

خلاصه‌ی جمع‌کننده‌های باینری

در این آموزش به جمع‌کننده‌های باینری پرداخته‌شد. این مدارهای جمع‌کننده، می‌توانند برای جمع دو عدد باینری با یکدیگر که یک خروجی نقلی، تولید می‌کنند؛ استفاده شود. در شکل پایه‌ی آن، جمع‌کننده‌ها می‌توانند با اتصال گیت Ex-OR و گیت AND به یکدیگر، ساخته‌شوند؛ که یک مدار نیم جمع‌کننده، تولید می‌کند. دو نیم جمع‌کننده که به یکدیگر، اتصال یابند؛ جمع‌کننده‌ی کامل، تولید می‌شود.

شماری از ICهای جمع‌کننده‎ی کامل 4 بیتی، مانند 74LS283 و CD4008 موجود می‌باشند؛ که دو عدد باینری 4 بیت را باهم جمع می‌کند و یک بیت ورودی نقلی اضافی و نیز یک بیت خروجی نقلی، فراهم می‌کند. پس می‌توان با کسکیدکردن آنها به یکدیگر، جمع‌کننده‌های 8 بیتی، 12بیتی و 16 بیتی، تولید نمود اما تاخیر انتشار نقلی، یک مسئله‌ی بزرگ در جمع‌کننده‌های موج‌دار n بیتی است.