وقتی خازنها در یک خط پشت سر هم به متصل میشوند، گفته میشود که سری هستند. برای خازنهای سری، جریان شارژ (iC) عبوری از آنها یکسان است، چراکه تنها یک مسیر برای عبور دارد.
پس خازنهای سری جریان مشابهی دارند که از طریق آنها جریان دارد: iT=i1=i2=i3=…. بنابراین هر خازن، بدون در نظر گرفتن ظرفیت، بار الکتریکی (Q) یکسانی را در صفحات خود ذخیره میکند. این بدان دلیل است که بار ذخیره شده در صفحه هر خازن، باید از صفحه خازن مجاور آن تامین شده باشد. بنابراین خازنهایی که به صورت سری به هم متصل میشوند باید از بار یکسانی برخوردار باشند.
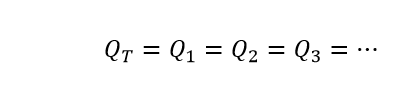
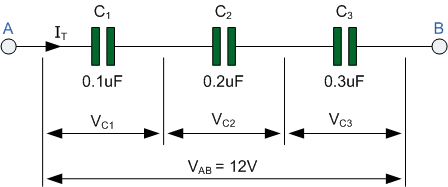
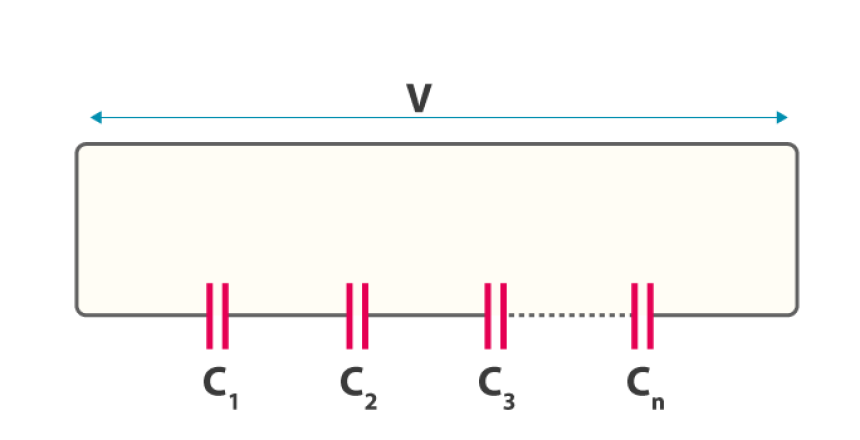
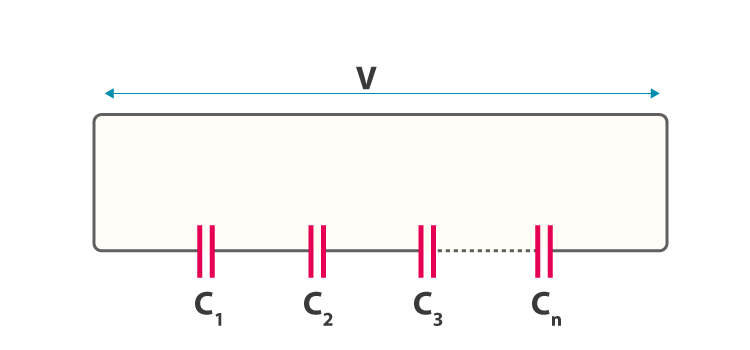
مدار زیر را در نظر بگیرید که در آن سه خازن C1، C2 و C3 به صورت سری به یک ولتاژ تغذیه بین نقاط A و B به هم متصل شدهاند.
خازنها در اتصال سری
در مدار موازی قبل دیدیم که ظرفیت کل (CT) مدار برابر است با مجموع کل خازنهای منفرد. با این وجود در یک مدار سری، ظرفیت کل یا معادل (CT) به شکل متفاوتی محاسبه میشود.
در مدار سری بالا، صفحه سمت راست خازن اول (C1) به صفحه سمت چپ خازن دوم (C2) متصل است و صفحه سمت راست آن به صفحه سمت چپ خازن سوم (C3) متصل است. پس این اتصال سری بدان معنی است که در یک مدار DC، خازن C2 عملا از مدار ایزوله است.
نتیجه این است که مساحت موثر صفحات به کمترین ظرفیت متصل در زنجیره سری کاهش یافته است. بنابراین افت ولتاژ هر خازن، بسته به مقادیر ظرفیتهای مختلف، متفاوت خواهد بود.
پس با اعمال قانون ولتاژ کیرشهف (KVL) در مدار بالا، به دست میآوریم:
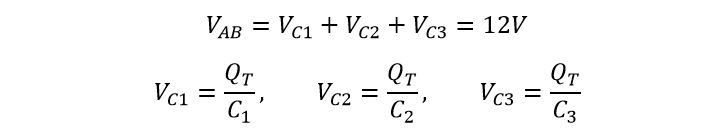
از آنجا که Q=C×V و پس از بازنویسی، V=Q/C، با جایگزین کردن VC با Q/C برای ولتاژ هر خازن در معادله KVL بالا داریم:
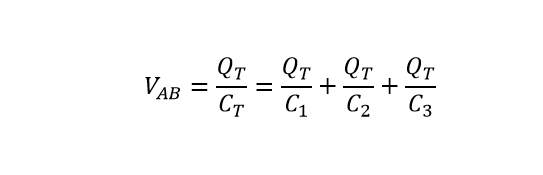
با تقسیم هر جمله بر QT داریم:
معادله خازنهای سری
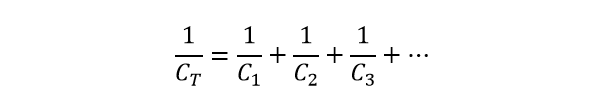
هنگام جمع کردن خازنهای سری، به جای خود ظرفیتها، معکوس (1/C) آنها با هم جمع میشود (دقیقا مانند مقاومتهای موازی). پس مقدار کل خازنهای سری برابر است با معکوس حاصل جمع معکوس ظرفیتها (به عبارت دیگر، معکوس ظرفیتها را با هم جمع کرده و حاصل آن را وارونه میکنیم).
اتصال سری خازنها، مثال 1
با در نظر گرفتن مقادیر سه خازن از مثال بالا، میتوانیم ظرفیت کل (CT) را برای سه خازن سری به صورت زیر محاسبه کنیم:
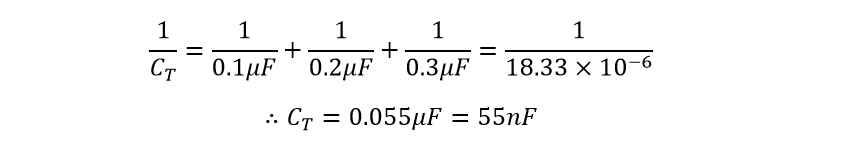
یک نکته مهم که در مورد خازنهایی که به صورت سری به هم متصل شدهاند باید به خاطر بسپارید، این است که ظرفیت کل مدار (CT) برای هر تعداد خازن متصل به هم در یک زنجیره سری، همواره کمتر از مقدار کوچکترین خازن در زنجیره است و در مثال بالا، CT=0.055μF در حالی که مقدار کوچکترین خازن در زنجیره سری 0.1μF است.
این روش معکوس محاسبه میتواند برای محاسبه هر تعداد خازن در یک شبکه سری استفاده شود. با این وجود، اگر تنها دو خازن در زنجیره سری وجود دارد، میتوان از یک فرمول بسیار سادهتر و سریعتر استفاده کرد و به صورت زیر ارائه میشود:
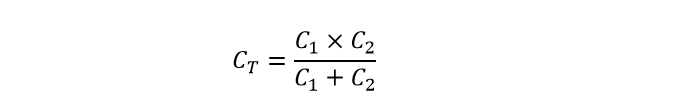
اگر دو خازن متصل به هم، برابر و دارای یک مقدار باشند، یعنی C1=C2، میتوانیم معادله بالا را به شرح زیر ساده کنیم تا ظرفیت کل ترکیب سری را پیدا کنیم.
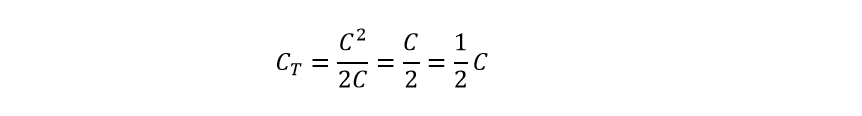
در این صورت میتوان دریافت که ظرفیت کل (CT) دقیقا برابر است با نصف مقدار یکی از خازنها، یعنی C/2، اگر و تنها اگر دو خازن متصل به هم، یکسان و برابر باشند.
برای مقاومتهای سری، مجموع کل افت ولتاژها در مدار سری برابر است با ولتاژ اعمال شده VS (قانون ولتاژ کیرشهف) و این در مورد خازنهای سری نیز صادق است.
در خازنهای سری، راکتانس خازنی به دلیل فرکانس تغذیه، به عنوان امپدانس عمل میکند. این راکتانس خازنی باعث افت ولتاژ در هر خازن میشود، بنابراین خازنهای سری به عنوان یک شبکه تقسیم ولتاژ خازنی عمل میکنند.
نتیجه این است که میتوان از فرمول تقسیم ولتاژ اعمال شده برای مقاومتها، برای یافتن ولتاژهای جداگانه برای دو خازن سری استفاده کرد. پس:

که در آن: CX ظرفیت خازن مورد نظر، VS ولتاژ تغذیه در زنجیره سری و VCX افت ولتاژ دو سر خازن هدف است.
اتصال سری خازنها، مثال 2
هنگامی که به منبع تغذیه 12 ولت AC متصل هستند، ظرفیت کلی و افت ولتاژ rms جداگانه را در مجموعه خازنهای سری زیر به دست آورید.
الف) دو خازن که ظرفیت هر کدام 47nF است
ب) یک خازن 470nF و یک خازن 1μF
الف) ظرفیت کل برابر

افت ولتاژ در دو خازن مشابه 47nF
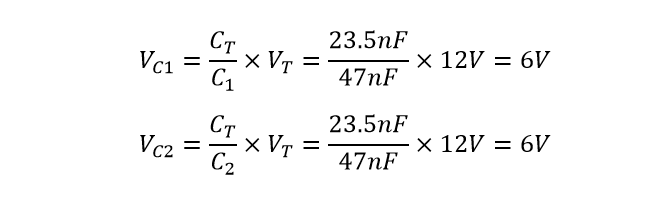
ب) ظرفیت کل نابرابر
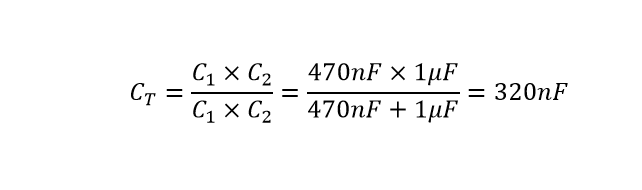
افت ولتاژ در دو خازن غیر مشابه، C1=470nF و C2=1μF
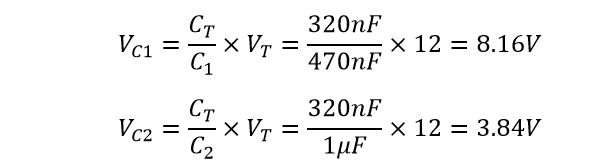
از آنجا که قانون ولتاژ کیرشهف در این مدار و هر مدار سری دیگر صدق میکند، جمع کل افت ولتاژها برابر با ولتاژ تغذیه (VS) خواهد بود. پس 8.16V+3.84V=12V.
همچنین توجه داشته باشید که اگر مقادیر خازن یکسان باشد، 47nF در مثال اول، همانطور که نشان داده شده، ولتاژ منبع تغذیه به طور مساوی بر روی هر خازن تقسیم میشود. دلیل این امر آن است که هر خازن در زنجیره سری، مقدار بار دقیقا مساوی (Q=C×V=0.564μC) در خود ذخیره میکند و بنابراین نیمی (یا درصدی برابر، برای بیش از دو خازن) از ولتاژ اعمال شده (VS) را دارد.
با این حال، هنگامی که مقادیر خازنهای سری متفاوت باشد، خازن بزرگتر، بار خود را با یک ولتاژ پایینتر و خازن کوچکتر، بار خود را با یک ولتاژ بالاتر شارژ میکند، در مثال دوم، این ولتاژها به ترتیب 3.84 و 8.16 ولت به دست آمدهاند. این اختلاف در ولتاژ، همانطور که نشان داده شده، باعث میشود که خازنها مقدار بار (Q) یکسانی در صفحات خود ذخیره کنند.
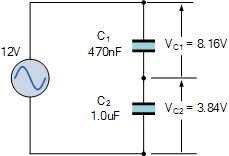

توجه داشته باشید که نسبت افت ولتاژ در دو خازن سری، بدون در نظر گرفتن فرکانس تغذیه، همواره یکسان خواهد بود، چراکه راکتانس (XC) آنها به طور نسبی ثابت خواهد ماند.
پس دو افت ولتاژ 8.16V و 3.84V در مثال ساده بالا یکسان خواهند ماند، حتی اگر فرکانس تغذیه از 100Hz به 100kHz افزایش یابد.
اگرچه افت ولتاژ هر خازن به ازای مقادیر مختلف، متفاوت خواهد بود، بار کولن ذخیره شده در صفحات برابر خواهد بود، زیرا جریان یکسانی در سراسر مدار سری وجود دارد و همه خازنها با تعداد یا کمیت یکسانی از الکترونها تغذیه میشوند.
به عبارت دیگر، اگر بار در صفحات هر خازن یکسان باشد، از آنجا که Q ثابت است، پس با کاهش ظرفیت، افت ولتاژ در صفحات خازن افزایش مییابد، زیرا بار نسبت به ظرفیت بزرگ است. به همین ترتیب، ظرفیت بزرگتر منجر به افت ولتاژ کمتری در صفحات خازن خواهد شد، زیرا بار نسبت به ظرفیت کم است.
خلاصه اتصال سری خازنها
پس برای جمع بندی: ظرفیت کل یا معادل (CT) مداری شامل خازنها سری، معکوس حاصل جمع معکوس ظرفیتهای خازنها است.
همچنین در خازنهای سری، همه خازنها دارای جریان شارژ یکسانی هستند، به طوری که iT=i1=i2=i3=…. دو یا چند خازن سری همواره دارای مقدار بار کولن برابر در صفحههای خود هستند.
از آنجا که بار (Q) برابر و ثابت است، افت ولتاژ خازن با تنها مقدار خازن تعیین میشود، چراکه V=Q/C. یک مقدار ظرفیت کوچک منجر به ولتاژ بزرگتر میشود، در حالی که مقدار ظرفیت بالا منجر به افت ولتاژ کمتری خواهد شد.






1 دیدگاه در “اتصال سری خازن ها”
عالی