فهرست مطالب
مدارهای تقسیمکنندهی جریان، دارای دو یا چند شاخهی موازی برای عبور جریانها میباشند؛ اما ولتاژ برای همهی عناصر موجود در مدار موازی، یکسان است.
مدارهای تقسیمکنندهی جریان، مدارهای موازی میباشند؛ که جریان منبع یا تغذیه را، به تعدادی مسیر موازی تقسیم میکنند. در یک مدار اتصال موازی، پایانههای تمام عناصر به یکدیگر متصلشده و دارای دو گرهی انتهایی یکسان میباشند. این امر، سبب ایجاد مسیرها و شاخههای مختلف برای شارش جریان یا عبور آن میشود. با اینحال، جریانها میتوانند مقادیر مختلفی برای هر عنصر، داشتهباشند.
ویژگی اصلی مدارهای موازی، ولتاژ یکسان در تمام مسیرهای اتصال مشترک ( … VR1 = VR2 = VR3)، درحالیاست که جریانهای متفاوتی در شاخههای مختلف، ایجاد میکنند. بنابراین، نیاز به یافتن ولتاژهای مقاومت منحصربفرد از طریق یافتن جریانهای شاخه ای، توسط قانون جریان کیرشهف (KCL) و قانون اهم برطرف میشود.
تقسیمکنندهی جریان مقاومتی
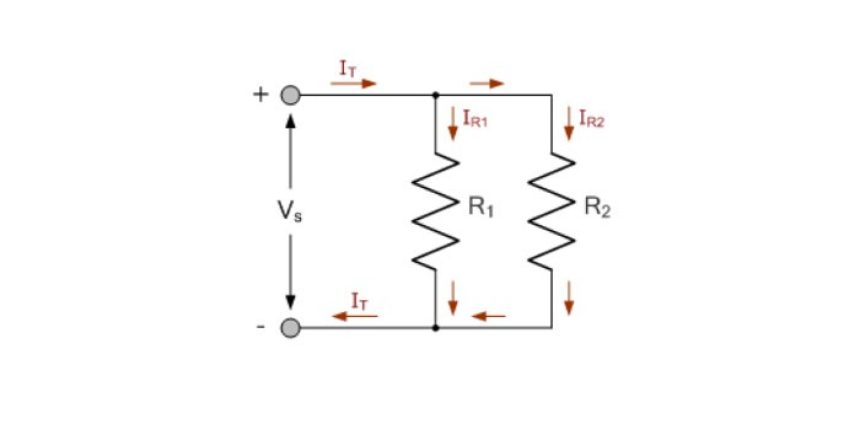
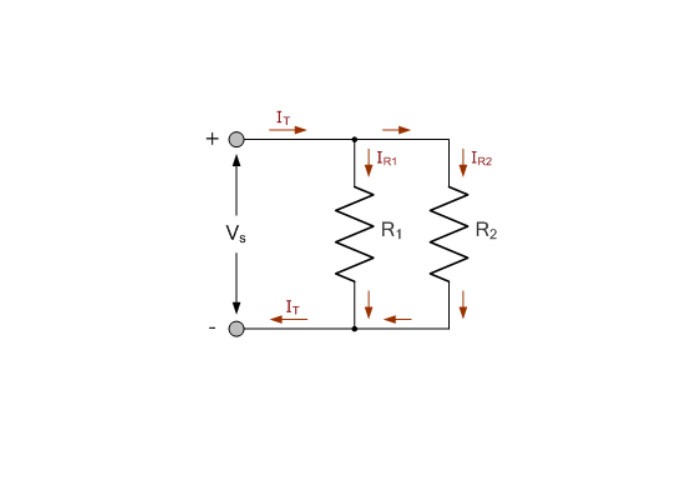
آسانترین برای فهم و پایهای ترین شکل شبکهی تقسیمکنندهی جریان پسیو، این است؛ که دو مقاومت به یکدیگر بهصورت موازی متصل شوند. قانون تقسیمکنندهی جریان، به ما اجازه میدهد؛ که شارش جریان را، در هر شاخهی موازی، بهعنوان درصدی از جریان کل، محاسبه کنیم. مدار زیر را درنظر بگیرید:
مدار تقسیمکنندهی جریان مقاومتی
دراینجا، یک مدار تقسیمکنندهی جریان پایه، از دو مقاومتR1 و R2، تشکیلشده است؛ که بهصورت موازی بههم متصل شدهاند و سبب جداشدن جریان منبع یا تغذیه IS بین آنها، به دو جریان جداگانهی IR1 و IR2 ،پیش از دوباره پیوستن آنها بهیکدیگر و برگشتن به منبع، میشود.
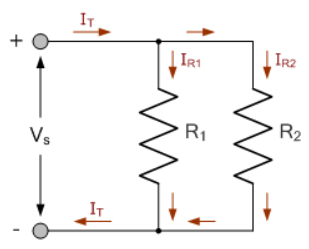
از آنجاییکه، جریان کل یا منبع، برابر با مجموع شاخههای منحصربفرد جریان میباشد؛ پس جریان کل، IT جاری در مدار، با استفاده از قانون جریان کیرشهف،KCL خواهدبود:
IT = IR1 + IR2
از آنجاییکه، دو مقاومت بهصورت موازی بههم متصل شدهاند؛ برای صدقکردن قانون جریان کیرشهف،KCL، باید جریان جاری در مقاومت R1 بهصورت زیر بدست آید:
IR1 = IT – IR2
و جریان جاری در مقاومت R2 نیز، بهصورت زیر بدست آید:
IR2 = IT – IR1
از آنجاییکه، یک مقدار ولتاژ V، دوسر هر عنصر مقاومتی، حضور دارد؛ باید جریان جاری را در هر مقاومت، نسبت به ولتاژ مشترک، از آنجاییکه، بهسادگی از قانون اهم، V = I*R تبعیت میکند؛ یافت. پس حل برای ولتاژ،V دوسر پیکربندی موازی به ما خواهد داد:
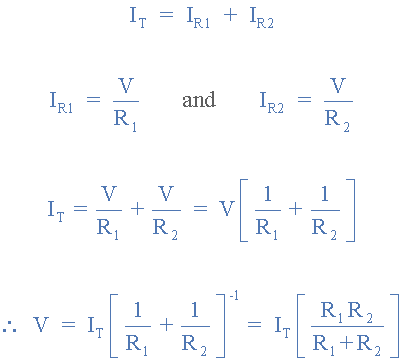
حال برای حل IR1 به ما خواهد داد:
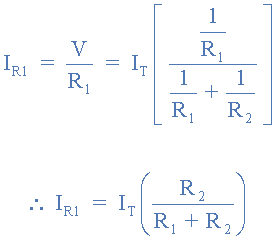
همینگونه برای حل IR2 به ما خواهد داد:
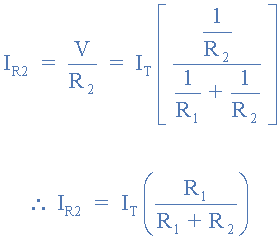
توجه داشتهباشید؛ که معادلات بالا برای هر جریان شاخهای، دارای عکس مقاومت در شمارندهی آن است. برای حل I1 از R2 و برای حل I2 از R1 استفاده میکنیم. دلیل آن، این است؛ که جریان هر شاخه با مقدار مقاومتی آن، نسبت عکس دارد و درنتیجه، مقدار مقاومتی کوچکتر، دارای جریان بزرگتر است.
مثال شمارهی 1 تقسیمکنندهی جریان
یک مقاومت ۲۰Ω، بهصورت موازی به یک مقاومت ۶۰Ω، متصل شدهاست. اگر این پیکربندی به دو سر منبع تغذیه باتری ،۳۰V متصل شدهباشد؛ جریان جاری در هر مقاومت و جریان کل تامینشده توسط منبع را بیابید.
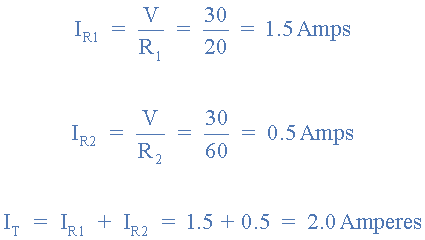
توجه داشتهباشید؛ که مقاومت کوچکتر ۲۰Ω دارای جریان بزرگتر است؛ زیرا براساس ماهیت خود، همیشه جریان بیشتری در مسیر یا شاخهی دارای کمترین مقاومت، جریان مییابد. این بدان معناست؛ که یک اتصال کوتاه، حداکثر جریان را ایجاد میکند، درحالیکه، یک مدارباز منجر به صفرشدن جریان میشود. به یاد داشتهباشید، که مقاومت معادل، REQ مقاومتهای اتصال موازی، همیشه کمتر از مقدار اهمی کوچکترین مقاومت است و با افزودن مقاومتهای موازی بیشتر، مقاومت معادل کاهش مییابد.
گاهی اوقات، محاسبهی همهی جریانهای شاخهای نیاز نیست؛ اگر جریان منبع تغذیه یا کل، IT شناخته شدهباشد. سپس جریان نهایی شاخه را، میتوان با تفریق جریانهای محاسبهشده از کل جریان، که طبق قانون جریان کیرشهف، تعریف شدهاست؛ پیدا نمود.
مثال شمارهی 2 تقسیمکنندهی جریان
سه مقاومت به یکدیگر متصل شدهاند؛ تا یک مدار تقسیمکنندهی جریان را بهصورت زیر، شکلدهند. اگر یک مدار، توسط یک منبع تغذیهی ۱۰۰ ولت و ۱/۵kW تغذیه شود؛ جریانهای هر شاخهی منحصربفرد را با استفاده از قانون تقسیم جریان و همچنین مقدار مقاومتی معادل مدار را، محاسبه کنید.
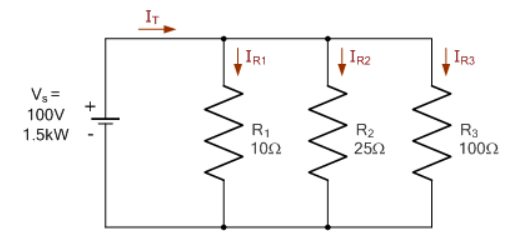
۱. جریان کل مدار: IT
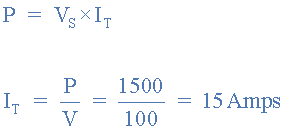
2. مقدار مقاومتی معادل:REQ
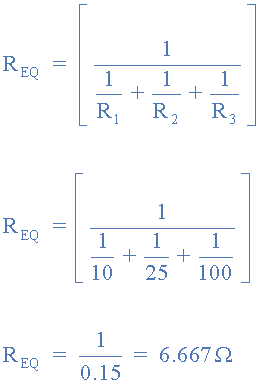
3. جریانهای شاخهای: IR3 ،IR2 ،IR1
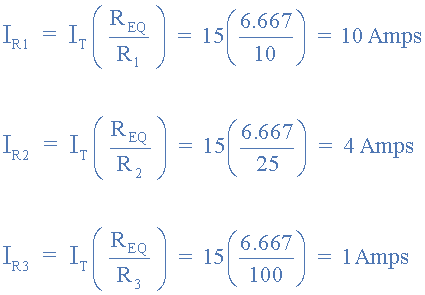
میتوانیم محاسبات خود را توسط قانون جریان کیرشهف چک کنیم؛ تمام جریانهای شاخهای، برابر با جریان کل، خواهد بود. پس طبق انتظار: آمپر IT = IR1 + IR2 + IR3 = 10 + 4 + 1 = 15 خواهدبود. بنابراین، میتوانیم ببینیم که جریان کل، IT طبق یک نسبت ساده، که توسط مقاومتهای شاخهای تعیین میشود؛ تقسیم میگردد. همچنین، با افزایش تعداد مقاومتهای اتصال موازی، جریان تغذیه یا کل، IT برای یک ولتاژ تغذیهی معین، VS افزایش مییابد؛ زیرا شاخههای موازی بیشتری، جریان دارند.
تقسیم جریان با استفاده از رساناییها
یک روش سادهی دیگر برای یافتن جریانهای شاخهای در مدار موازی، این است؛ که از روش رسانایی، استفاده کنیم. در مدارهای DC، رسانایی عکس مقاومت است و با حرف “G” نشان داده میشود. از آنجاییکه، رسانایی(G) معکوس مقدار مقاومتی(R) است؛ که برحسب اهم اندازهگیری میشود، معکوس اهم را “موهو”(Ʊ)( علامت معکوس اهم) مینامند. بنابراین، G = 1/R است و یکای الکتریکی دادهشده به رسانایی، زیمنس(S) خواهدبود.
پس برای مقاومتهای اتصال موازی، رسانایی معادل یا کل، CT برابر با مجموع رساناییهای منحصربفرد، بهصورت زیر خواهدبود.
رسانایی موازی
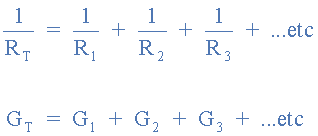
بنابراین، اگر مقدار مقاومتی، دارای مقدار ثابت ۱۰Ω باشد؛ رسانایی معادل برابر با ۰/۱S خواهد بود و همینگونه، ادامه خواهدداشت. بهدلیل معکوسبودن، یک رسانایی مقدار بالا، نشاندهندهی مقدار مقاومتی کم و برعکس است. همچنین میتوانیم از پیشوند برای شکلدهی مقادیر کوچک رسانایی مانند، میلی زیمنس،mS، میکرو زیمنس، uS و حتی نانو زیمنس، nS استفاده کنیم.
با استفاده از قانون اهم برای جریان، که در واقع I = V/R است؛ میتوان جریانهای شاخهای را، بااستفاده از رسانایی بهصورت I = V*G بهدست آورد.
در واقع، میتوانیم این امر را، با ارائهی اینکه جریان تغذیه در شبکهی موازی مقاومتی ما بهصورت زیر است، یک گام جلو ببریم:
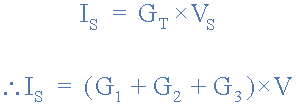
اما از بالا، میدانیم که برای یک مدار اتصال موازی، ولتاژ در همهی عناصر، مشترک است و از آنجاییکه، ولتاژ، برابر با جریان ضربدر مقدار مقاومتی، V = I*R، است. میتوانیم نتیجه بگیریم؛ که هنگام استفاده از رسانایی، ولتاژ، برابر با جریان تقسیم بر رسانایی، یعنی V = I/G است.
پس میتوانیم معادلات بالا را، برای قانون تقسیمکنندهی جریان، از طریق رسانایی (G) بهجای مقدار مقاومتی (R) بهصورت زیر بیان کنیم:
قانون تقسیمکنندهی جریان با استفاده از رسانایی
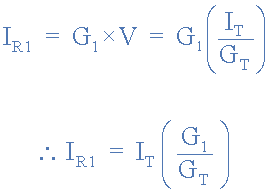
بههمین ترتیب، برای جریانهای مقاومتهای موازی R2 و R3 بهصورت زیر، بهدست خواهیم آورد:
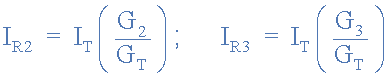
ممکن است تا الان متوجه شدهباشید؛ که برخلاف معادلات بالا برای مقدار مقاومتی، هر جریان شاخهای، دارای مقدار رسانایی یکسانی در شمارندهی خود است. از اینرو، برای حل I1 از G1 و برای حل I2 از G2 استفاده میکنیم. دلیل آن، این است؛ که رساناییها، معکوس مقادیر مقاومتی میباشند.
مثال شمارهی 3 تقسیمکنندهی جریان
با استفاده از روش رسانایی، جریانهای شاخهای منحصربفرد،I2، I1 و I3 را برای مدار مقاومتی موازی زیر بیابید.
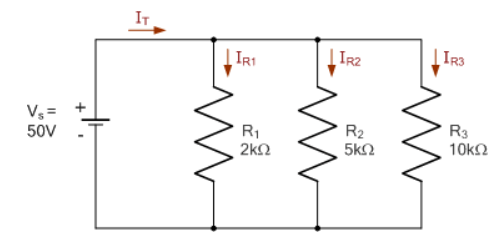
رسانایی کل: GT
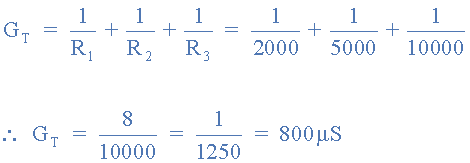
جریان کل منبع تغذیه: IS
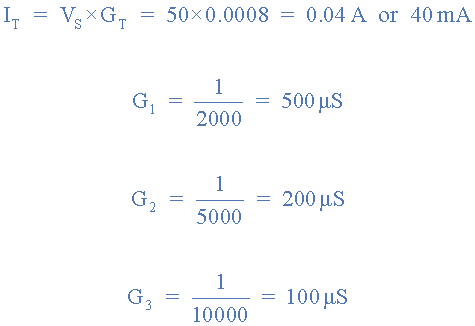
جریانهای شاخهای منحصر بفرد: IR3 ،IR2 ،IR1
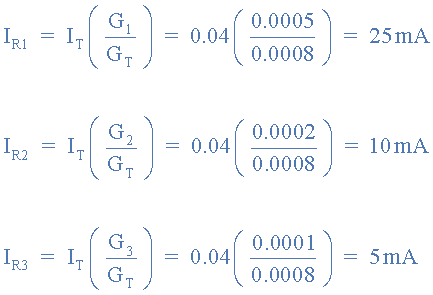
ازآنجاییکه، رسانایی، معکوس مقدار مقاومتی است؛ مقدار مقاومتی معادل مدار نمونه، بهسادگی ۱/۸۰۰uS بوده که برابر با ۱۲۵۰Ω یا ۱/۲۵kΩ است؛ که بهروشنی کمتر از کوچکترین مقدار مقاومت R1 یعنی 2kΩ است.
خلاصهی تقسیمکنندهی جریان
تقسیمکنندههای جریان یا تقسیم جریان، فرآیند یافتن جریانهای شاخهای جداگانه، در یک مدار موازی است؛ درصورتی که هر عنصر موازی، دارای ولتاژ یکسانی باشد. قانون جریان کیرشهف (KCL) بیان میکند؛ که جمع جبری جریانهای منحصربفرد ورودی به اتصال یا گره، برابر با جریانهای خروجی از آن است. یعنی نتیجهی خالص برابر با صفر است.
قانون تقسیمکنندهی جریان کیرشهف، میتواند برای یافتن جریانهای شاخهای منحصربفرد، هنگامیکه مقدار مقاومتی معادل و جریان کلی مدار شناختهشدهباشند؛ مورداستفاده قرارگیرد. هنگامیکه، دو مقدار مقاومتی درگیر باشند؛ جریان در هر شاخه، بخشی از مقدار کل جریان، IT خواهدبود. اگر دو شاخهی موازی مقاومتی، دارای مقدار یکسانی باشند؛ جریان بهصورت مساوی، تقسیم میشود.
درمورد سه یا چند شاخهی موازی، مقدار مقاومتی معادل، REQ برای تقسیم جریان کل به کسرهایی از جریان برای هر شاخه، استفاده میشود؛که نسبتی از جریان را، تولید میکند؛ که برابر با معکوس مقادیر مقاومتی بوده و سبب تولید بزرگترین مقدار جریان از کمترین مقدار مقاومتی میگردد. جریان کل یا منبع، IT برابر با مجموع جریانهای شاخهای منحصربفرد است. این امر، سبب میشود؛ تقسیمکنندههای جریان برای استفاده با منابع جریان، مفید باشند.
گاهی اوقات، استفاده از رسانایی در مدارهای موازی، راحتتر است؛ زیرا میتواند به کاهش محاسبات ریاضیاتی موردنیاز برای تعیین جریان شاخهای، از طریق عناصر مدار جداگانه، که بهصورت موازی متصل شدهاند؛ کمک کند. و دلیل آن این است؛ که در مدارهای موازی، رسانایی کل، برابر با مقادیر رسانایی منحصربفرد است. رسانایی، معکوس مقدار مقاومتی، یعنی G = 1/R میباشد و یکای آن، زیمنس S است. رسانایی یک عنصر، میتواند هم برای منبع تغذیه ولتاژ DC و هم AC، در تقسیمکنندههای جریان استفاده شود.