رابطه بین ولتاژ، جریان و رزیستانس، در هر مدار الکتریکی DC، درابتدا توسط فیزیکدان آلمانی، جورج اهم کشف شد.
جورج اهم دریافت که در یک دمای ثابت، شارش جریان الکتریکی در یک مقاومت خطی ثابت، به صورت مستقیم با ولتاژ دو سر آن و نیز، با مقاومت، به صورت معکوس متناسب است. این رابطه بین ولتاژ، جریان و رزیستانس، اساس قانون اهم را شکل میدهد؛ که در زیر آورده شده است.
رابطهی قانون اهم
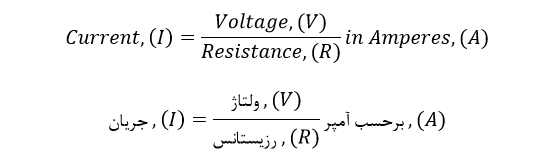
با دانستن هر دو مقدار از مقادیر ولتاژ، جریان یا مقاومت، میتوانیم از قانون اهم برای یافتن سومین مقداری که موجود نیست استفاده کنیم. قانون اهم، به طور گسترده در فرمولها و محاسبات الکترونیک استفاده میشود؛ بنابراین “درک و به خاطر سپردن دقیق این فرمولها بسیار مهم است”.
برای یافتن ولتاژ (V)
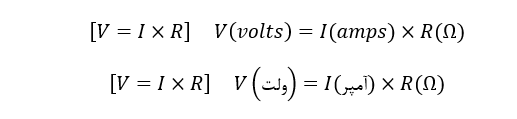
برای یافتن جریان (I)
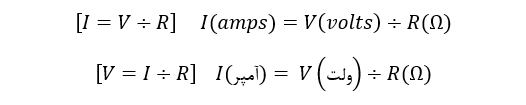
برای یافتن رزیستانس (R)
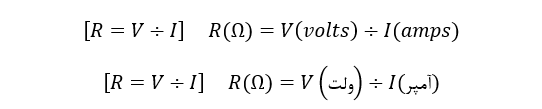
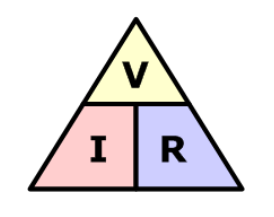
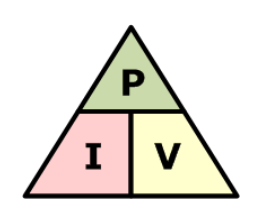
گاهی اوقات، به راحتی میتوان این رابطهی قانون اهم را با استفاده از تصاویر به خاطر آورد. در اینجا، سه مقدار V، I و R بر روی مثلث قرار گرفتهاند (مثلث، مثلث قانون اهم نامیده میشود) که در بالا ولتاژ، جریان و مقاومت در پایین، نشان داده شدهاند. این چیدمان، نشان دهندهی موقعیت واقعی هر کمیت در فرمولهای قانون اهم است.
مثلث قانون اهم
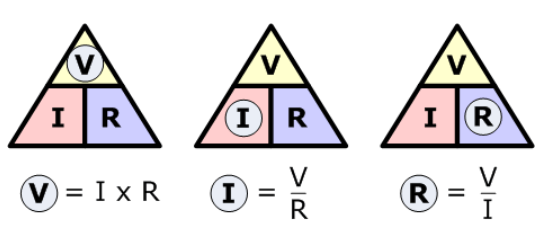
با جابهجایی معادلهی استاندارد قانون اهم در بالا، ترکیبهای زیر از همان معادله به ما داده میشود:
پس با استفاده از قانون اهم، میتوانیم مشاهده کنیم که 1 ولت، ولتاژ اعمال شده، به یک مقاومت 1Ω ،باعث جریان 1 آمپر میشود و هر چه مقدار مقاومت بیشتر باشد، میزان جریان کمتری برای یک ولتاژ اعمال شده معین جریان مییابد. در هر وسیلهی الکتریکی یا عنصری که از “قانون اهم” پیروی میکند، شارش جریان جاری در آن، متناسب با ولتاژ دو سر آن، (I α V) مانند مقاومتها یا کابلها بوده، که از نظر ماهیت “اهمی” میباشند و دستگاههایی که اینگونه نیستند مانند دستگاههای ترانزیستورها و دیودها، دستگاه های “غیر اهمی” نامیده میشوند.
توان الکتریکی در مدارها
توان الکتریکی (P)، در یک مدار، میزان جذب یا تولید انرژی در یک مدار است. یک منبع انرژی مانند ولتاژ، توان تولید یا عرضه میکند؛ در حالیکه، بار متصل شده، آن را جذب میکند. به عنوان مثال، لامپها و بخاریها، توان الکتریکی را جذب کرده و آن را به گرما، نور و یا هر دو تبدیل میکنند. هر چه مقدار یا نرخ آنها بر حسب وات بیشتر باشد؛ احتمالا توان الکتریکی بیشتری مصرف خواهند کرد.
نماد کمیت برای توان، P بوده و حاصل ضرب ولتاژ در جریان است. واحد اندازهگیری آن وات (W) است. پیشوندهایی که برای نشان دادن مضربهای متعدد یا پیشوند های وات استفاده میشوند؛ مانند میلیوات (mW=10-3W) یا کیلو وات (kW=103W) میباشند.
پس با استفاده از قانون اهم و جایگذاری مقادیر V،I و R میتوان فرمول توان الکتریکی را بهصورت زیر یافت:
برای یافتن توان (P)
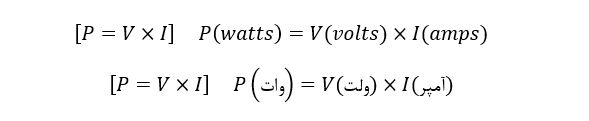
همچنین:
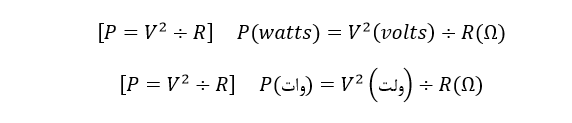
همچنین:
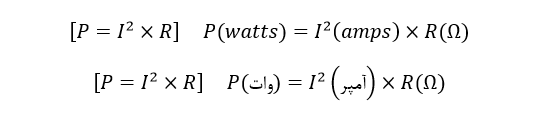
دوباره سه کمیت، مثلث توان را تشکیل میدهند؛ که توان در بالا و ولتاژ و جریان در پایین است. دوباره، این چیدمان نشاندهندهی وضعیت واقعی هر کمیت برحسب فرمولهای قانون اهم است.
مثلث توان
و دوباره، جابهجایی معادلهی اساسی قانون اهم در بالا برای توان، ترکیبهای زیر از یک معادله را، برای یافتن مقادیر مختلف منحصر بفرد به ما میدهد:
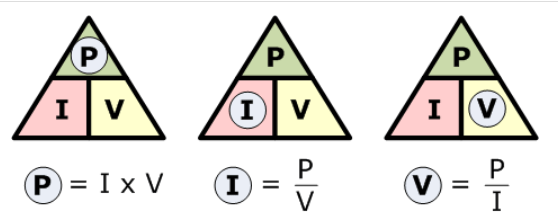
بنابراین میتوانیم ببینیم که سه فرمول محاسبهی توان الکتریکی در مدار وجود دارد. اگر مقدار توان محاسبهشده مثبت باشد (+P)، برای هر فرمولی عنصر توان جذب میکند. این استفاده یا مصرف توان است. اما اگر مقدار توان محاسبه شده منفی باشد (-P)؛ عنصر توان تولید یا ایجاد میکند، به بیان دیگر این منبع توان الکتریکی، مانند باتریها و ژنراتورها است.
نرخ توان الکتریکی
قطعات الکتریکی دارای “نرخ توان” بر حسب وات میباشند که نشاندهندهی حداکثر نرخی است، که یک عنصر، توان الکتریکی را به شکلی از انرژی مانند گرما، نور یا حرکت تبدیل میکند. برای مثال، یک مقاومت 1/4 وات و یک لامپ 100 وات و غیره.
همچنین، اکنون میدانیم که یکای توان، وات است؛ اما برخی از دستگاههای الکتریکی مانند موتورهای الکتریکی، دارای نرخ توان در اندازه گیری قدیمی “اسب بخار” یا hp میباشند. رابطهی بین اسب بخار و وات بهصورت: 1hp=746W است. پس برای مثال، دو موتور اسببخار دارای نرخ 1492W،(2*746) یا 1.5KW است.
نمودار پای قانون اهم
برای کمک به فهم بهتر رابطهی بین مقادیر مختلف، میتوانیم همه معادلات قانون اهم را از بالا، برای یافتن ولتاژ، جریان، رزیستانس و توان دریافت کرده. و آنها را در یک نمودار پای قانون اهم، برای استفاده از مدارهای AC و DC ببریم و محاسبات آنها را بهصورت زیر نشان دهیم:
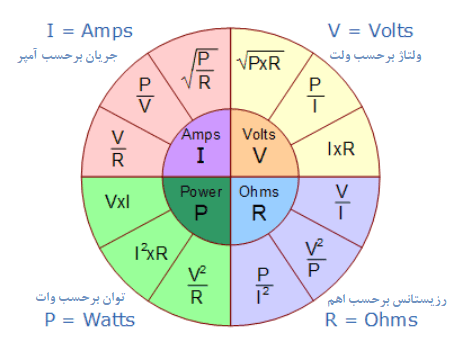
علاوهبر استفاده از نمودار پای قانون اهم نشاندادهشده در بالا، ما همچنین میتوانیم معادلات منحصربفرد قانون اهم را، در یک جدول ماتریس ساده برای مراجعهی آسان، هنگام محاسبهی مقدار نامعلوم قرار دهیم.
جدول ماتریس قانون اهم
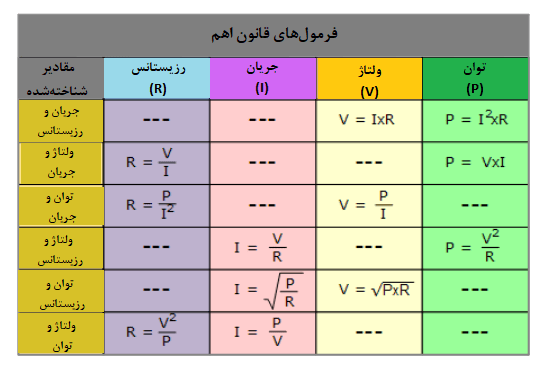
مثال 1
برای مداری که در پایین نشان دادهشده است؛ ولتاژ (V)، جریان (I)، رزیستانس (R) و توان (P) را بیابید.
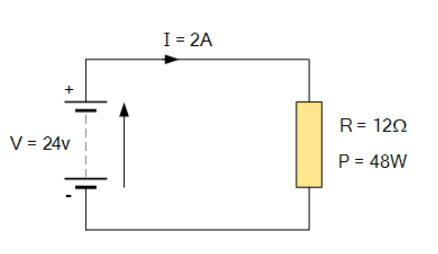
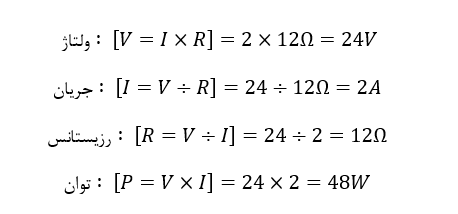
توان در یک مدار الکتریکی، تنها زمانی وجود دارد؛ که ولتاژ و جریان هردو موجود باشند. برای مثال، در یک وضعیت مدارباز، ولتاژ زمانی وجود دارد؛ که شارش جریان برابر با صفر(I=0) باشد. از اینرو، V*0 برابر با 0 بوده و توان تلفشده در مدار، برابر با صفر است. به همینترتیب، اگر وضعیت اتصال کوتاه داشته باشیم؛ شارش جریان وجود دارد؛ اما ولتاژ، برابر با صفر (V=0) است و 0*I=0، بنابراین توان تلفشده در مدار برابر با 0 است.
از آنجایی که، توان الکتریکی، حاصلضرب V*I بوده و توان تلفشده در مدار، چه درصورت ولتاژ بالا و جریان کم و چه درصورت ولتاژ کم و جریان بالا، برابر است. درحالتکلی، توان الکتریکی تلفشده در شکل گرما (هیتر)، کار مکانیکی مانند موتورها، انرژی بهصورت تابش (لامپها) یا بهعنوان انرژی ذخیرهشده (باتریها) تلف میشود.
انرژی الکتریکی در مدارها
انرژی الکتریکی، ظرفیت انجام کار است و یکای کار با انرژی، ژول (J) است. انرژی الکتریکی حاصل ضرب توان در مدت زمان مصرف است. بنابراین، اگر بدانیم چه مقدار توانی برحسب وات مصرف شدهاست و چه مقدار زمان، برحسب ثانیه، برای آن استفاده میشود، میتوانیم کل انرژی مصرفی را در وات ثانیه پیدا کنیم.
به بیان دیگر، زمان * توان = انرژی و جریان * ولتاژ = انرژی است. از اینرو، توان الکتریکی، مرتبط با انرژی و یکای انرژی الکتریکی، وات-ثانیه یا ژول است.
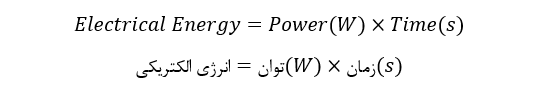
توان الکتریکی را میتوان بهعنوان نرخ انتقال انرژی تعریف کرد. اگر یک ژول کار، با نرخ ثابت یک ثانیه جذب یا تحویل داده شود؛ توان مربوطه معادل یک وات خواهد بود. بنابراین، توان را میتوان “1وات=ثانیه/1ژول” تعریف کرد. پس میتوان گفت؛ که یک وات معادل یک ژول در ثانیه است و توان الکتریکی را، میتوان بهعنوان میزان انجام کار یا انتقال انرژی تعریف کرد.
توان الکتریکی و مثلث انرژی
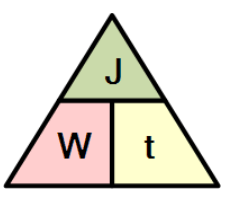
برای یافتن کمیتهای مختلف منحصر بفرد:
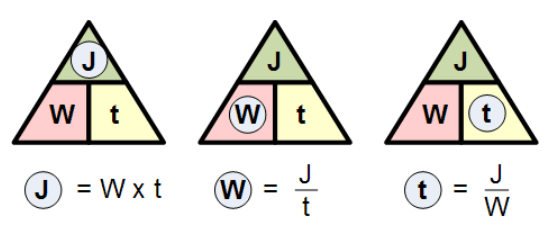
پیش از این گفتیم که انرژی الکتریکی برحسب وات-ثانیه یا ژول تعریف میشود. اگرچه، انرژی الکتریکی برحسب ژول اندازهگیری میشود؛ اما وقتی برای محاسبهی انرژی مصرفی یک عنصر، مورد استفاده قرار میگیرد، میتواند به مقدار بسیار بزرگی تبدیل شود.
برای مثال، اگر یک لامپ 100وات برای 24ساعت، روشن گذاشتهشود، انرژی مصرفی برابر با 8640000 ژول (100W*86400s) خواهد بود و بنابراین پیشوندهایی مانند کیلوژول (kJ=103J) یا مگاژول (MJ=106J) به جای آن استفاده میشود و در این مثال، انرژی مصرفی برابر با 8.64MJ (مگاژول) است.
هنگام سروکار داشتن با ژول، کیلوژول و مگاژول برای بیان انرژی الکتریکی، ریاضیات مربوطه میتواند دارای اعداد بزرگ و صفرهای زیادی باشد و بنابراین، بیان انرژی الکتریکی مصرفشده برحسب کیلووات-ساعت بسیار آسانتر است.
اگر توان الکتریکی مصرفی (یا تولیدشده) برحسب وات یا کیلووات (هزاروات) اندازه گیری شود و زمان بر حسب ساعت و نه ثانیه محاسبه گردد، پس یکای انرژی الکتریکی برابر با کیلووات-ساعت (kWhr) خواهد بود. پس لامپ 100وات ما در بالا، 2400 وات-ساعت یا 2.4kWhr مصرف خواهد کرد؛ که برای فهم 8640000 ژول، آسانتر است.
1 کیلووات-ساعت (1kWh)، میزان برق مصرفی دستگاهی است که نرخ آن، 1000 وات در یک ساعت است و معمولا بهصورت “واحد برق”، خوانده میشود. این چیزی است؛ که با کنتوربرق اندازهگیری میشود و ما بهعنوان مصرفکننده، هنگام دریافت قبض از تامینکنندگان برق، میپردازیم.
کیلووات-ساعت، یکای استاندارد انرژی است؛ که توسط کنتور برق در خانههای ما برای محاسبهی میزان انرژی الکتریکی مورد مصرف ما، استفاده شده و در نتیجه طبق آن، هزینه را میپردازیم. اگر یک آتش الکتریکی را با المنت حرارتی روشن کنیم و نرخ آن 1000 وات باشد و برای یک ساعت روشن بماند، الکتریسته مصرفی آن 1kWh خواهد بود و اگر دو آتش الکتریکی که هرکدام المنت 1000وات دارند؛ برای نیمساعت روشن کنیم؛ کل مصرف، دقیقا برابر با همان میزان برق، 1kWh خواهد بود.
پس، برای مصرف 1000 وات در یک ساعت، همان مقدار توانی را مصرف مینماید؛ که برای 2000 وات (2 برابر) برای نیمساعت(نصف زمان) مصرف میکند. پس برای مصرف 1kWh یا یک واحد انرژی الکتریکی، در یک لامپ 100 وات، نیاز به روشن نگه داشتن آن به مدت 10 ساعت (10*100=1000=1kWhr) است.
حال که رابطهی بین ولتاژ، جریان و رزیستانس را در مدار میدانیم، در آموزش بعدی مرتبط با مدارهای DC، به یکاهای استاندارد الکتریکی مورد استفاده در مهندسی برق و الکترونیک، که ما را قادر به محاسبهی این مقادیر میسازد؛ پرداخته و خواهیم دید که هر مقدار را میتوان به صورت مضرب یا پیشوندهای هر یکای استاندارد نشان داد.