در آموزش مرتبط با مقاومتها دیدیم که یک مقاومت معادل واحد (RT)، زمانی پیدا میشود که دو یا چند مقاومت، در اتصال سری یا موازی یا ترکیبی از هردو، با یکدیگر باشند و مدارها از قانون اهم پیروی کنند.
با اینحال، گاهی اوقات، در مدارهای پیچیده مانند شبکههای پل یا شبکههای T، نمیتوانیم به تنهایی از قانون اهم برای یافتن ولتاژها یا جریانهای مدار استفاده کنیم. برای این نوع از محاسبات، نیاز به قانونهای خاصی داریم که به ما اجازه دهد تا معادلات مدار را به دست بیاوریم و برای این کار میتوانیم از قانون مداری کیرشهف استفاده کنیم.
درسال 1845، گوستاو کیرشهف، فیزیکدان آلمانی، یک جفت یا مجموعهای از قوانین را، برای حفظ جریان و انرژی در مدارهای الکتریکی ایجاد کرد. این دو قانون عموما به این نامها شناخته میشوند: از قانونهای مداری کیرشهف، قانونی که مرتبط با شارش جریان در یک مداربسته است؛ را قانون جریان کیرشهف (KCL) میگویند. و قانون دیگری که با منابع ولتاژ حاضر در مدار بسته سروکار دارد، قانون ولتاژ کیرشهف (KVL) است.
قانون اول کیرشهف - قانون جریان (KCL)
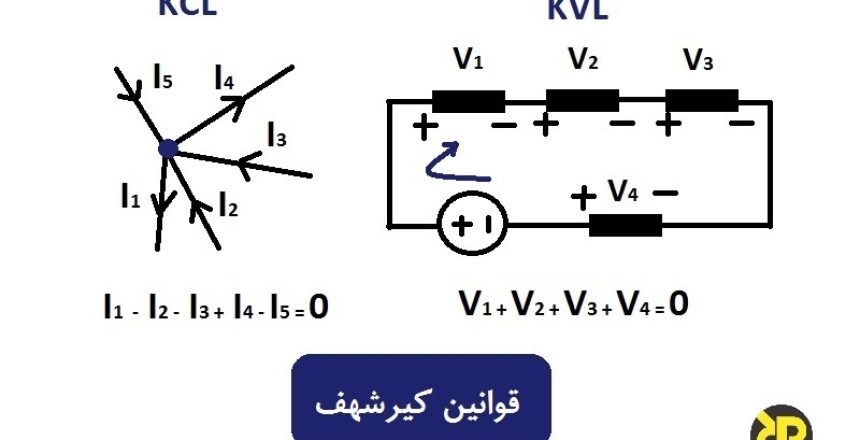
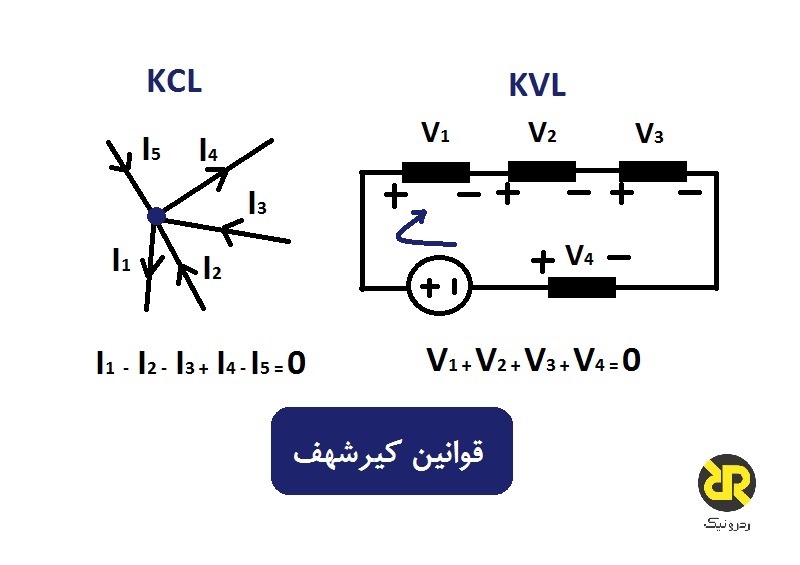
قانون جریان کیرشهف یا KCL، بیان میکند که “کل جریان یا شارژ ورودی به یک اتصال یا گره، دقیقا برابر با شارژ خروجی از آن گره است؛ چون هیچ باری در گره از بین نمیرود، راهی بهجز خروج ندارد“. به بیان دیگر، مجموع جبری تمام جریانهای ورودی و خروجی گره، باید برابر با صفر باشد (0=خروجیI +ورودیI). این ایده کیرشهف، معمولا بهعنوان حفظ شارژ، شناخته میشود.
قانون جریان کیرشهف
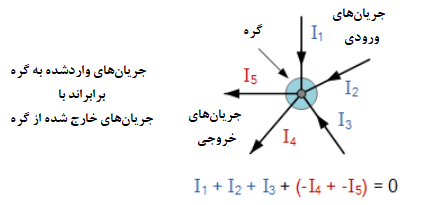
در اینجا، سه جریان ورودی به گره I1 ،I2 و I3 از نظر مقداری مثبت و دو جریان خروجی گره I4 و I5 از نظر مقداری منفی میباشند. معادلهی آن را بهصورت زیر مینویسیم:
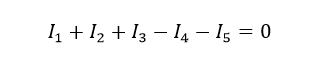
در یک مدار الکتریکی اصطلاح گره، به طور کلی، به اتصال یا محل برخورد دو یا چند جریان در مسیرها یا عناصری، مانند کابل و اجزای مدار اشاره دارد. برای شارش جریان در داخل یا خارج یک گره، باید یک مسیر مدار بسته وجود داشتهباشد. هنگام تجزیه و تحلیل مدارهای موازی، میتوانیم از قانون جریان کیرشهف استفاده کنیم.
قانون دوم کیرشهف - قانون ولتاژ (KVL)
قانون ولتاژ کیرشهف یا KVL، بیان میکند که “در هر شبکهی حلقه بسته، ولتاژ کل در حلقه، برابر با مجموع افت ولتاژها، در همان حلقه است“که برابر با صفر است. به بیان دیگر، مجموع جبری تمام ولتاژهای درون حلقه، باید برابر با صفر باشد. این ایده کیرشهف معمولا بهعنوان حفظ انرژی شناخته میشود.
قانون ولتاژ کیرشهف
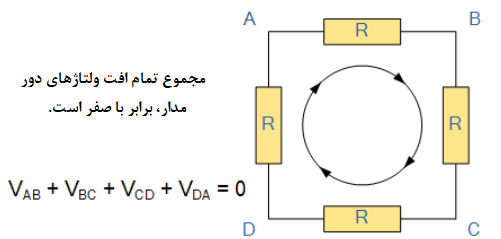
از هر نقطه ای که در مدار شروع کردید در همان جهت ادامه داده و جهت تمام افت ولتاژها را، چه مثبت و چه منفی یادداشت نموده و به نقطه ابتدایی بازگردید. بسیار حائز اهمیت است که در یک جهت، چه ساعتگرد و چه پادساعتگرد بمانید؛ در غیر این صورت مجموع ولتاژهای نهایی برابر با صفر نخواهد شد. هنگام تجریه و تحلیل مدارهای سری، میتوانیم از قانون ولتاژ کیرشهف استفاده کنیم.
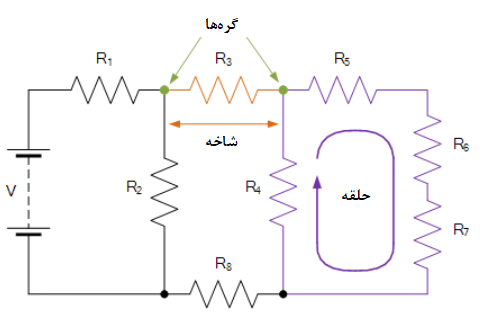
هنگام تجزیه و تحلیل مدارهای DC یا مدارهای AC، با استفاده از قوانین مداری کیرشهف، تعدادی تعاریف و اصطلاحات برای توصیف بخشهای تجزیه و تحلیلی مدار، مانند: گره، مسیر، شاخه، حلقه و مش استفاده میشوند. از این اصطلاحات اغلب به کار برده شده بنابراین درک آنها مهم است.
اصطلاحات عمومی نظریهی مدار DC
- مدار – یک مدار، یک مسیر هدایت حلقه بسته برای شارش جریان الکتریکی در آن است.
- مسیر – یک خط منحصربفرد و متصلکنندهی عناصر یا منابع است.
- گره – یک گره، محل برخورد، اتصال یا پایانه درون یک مدار است؛ که دو یا تعداد بیشتری عناصر مداری را به هم متصل کرده یا پیوند میدهد و سبب ایجاد یک نقطهی اتصال بین دو یا تعداد بیشتری شاخه میگردد. یک گره با یک نقطه نمایش داده میشود.
- شاخه – یک شاخه، یک یا گروهی از اجزای مدار مانند مقاومت یا منبع است که بین دو گره به هم متصل شدهاند.
- حلقه – یک حلقه، یک مسیر بسته ساده در یک مدار است که در آن بیش از یک بار، با هیچ عنصر یا گرهای از مدار، برخورد صورت نمیگیرد.
- مش- یک مش، یک مسیر سری حلقهی بستهی ساده است؛ که هیچ مسیر دیگری را شامل نمیشود. هیچ حلقهای داخل مش، وجود ندارد.
توجه داشته باشید که:
اگر مقدار جریان در تمام عناصر مدار یکسان باشد؛ گفته میشود که عناصر، به صورت سری به یکدیگر متصل شدهاند.
اگر مقدار ولتاژ دو سر تمام عناصر مدار یکسان باشد؛ گفته میشود که عناصر، به صورت موازی به یکدیگر متصل شدهاند.
مثالی از یک مدار معمولی DC
مثال 1
جریان جاری در مقاومت (40Ω) R3 را بیابید.
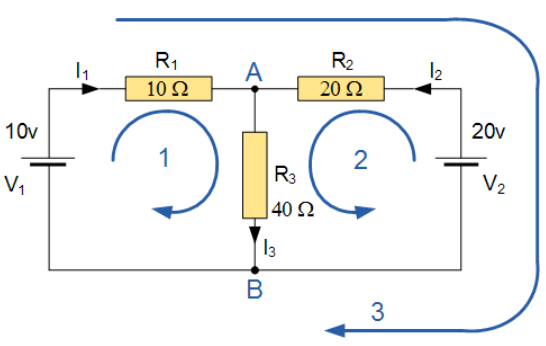
مدار دارای 3 شاخه، 2 گره (A و B) و 2 حلقهی منحصر بفرد است.
با استفاده از قانون جریان کیرشهف، KCL، معادلات زیر را خواهیم داشت:
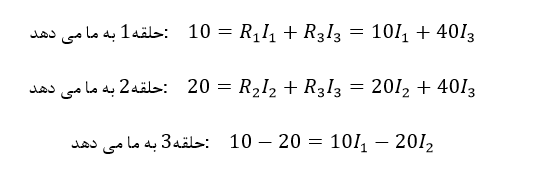
از آنجایی که I3 مجموع I1+I2 است؛ میتوانیم معادلات را دوباره بنویسیم:
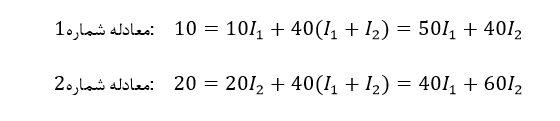
پس ما در حال حاضر، دو “معادلهی همزمان“ داریم که میتوان آنها را کاهش داد و مقادیر I1 و I2 را بهدست آورد.
جایگذاری I1 برحسب I2 به ما مقدارِ آمپر I1=-0.143 را میدهد.
جایگذاری I2 برحسب I1 به ما مقدارِ آمپر I2=+0.429 را میدهد.
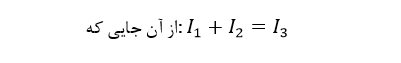
جریان جاری در مقاومت R3 برابر است با: آمپر -0.143 + 0.429 = 0.286
ولتاژ دوسر مقاومت R3 برابر است با: ولت 0.286 * 40 = 11.44
علامت منفی برای I1، به این معناست که جهت جریان جاری، در ابتدا اشتباه درنظر گرفته شده بود؛ اما همچنان معتبر است. در واقع باتری 20 ولت، باتری 10 ولت را شارژ میکند.
کاربردهای قوانین مدار کیرشهف
این دو قانون، امکان یافتن جریانها و ولتاژها در یک مدار را فراهم میکند. یعنی گفته میشود که مدار “تجزیه و تحلیل شدهاست” و روش اساسی برای استفاده از قوانین مداری کیرشهف به شرح زیر است:
- فرضکنید که همه ولتاژها و مقاومتها، داده شدهاست (اگر اینگونه نبود، به آنها برچسب V1، V2 و…. R1،R2 و… بزنید )
- یک جریان را به هر شاخه یا مش اختصاص دهید (ساعتگرد یا پادساعتگرد)
- به هر شاخه همراه با جریان آن، برچسب بزنید (I1،I2، I3و…)
- معادلات قانون اول کیرشهف را برای هر گره بیابید.
- معادلات قانون دوم کیرشهف را، برای هر حلقهی منحصربفرد در مدار بیابید.
- از معادلات همزمان خطی، برای یافتن جریانهای مجهول لازم استفاده کنید.
علاوه بر استفاده از قانون مداری کیرشهف، برای محاسبهی ولتاژها و جریانهای مختلف در یک مدار خطی، میتوانیم از تجزیه و تحلیل حلقه، برای محاسبهی جریانها در هر حلقهی منحصربفرد استفاده کنیم؛ که مقدار ریاضیات مورد نیاز را با استفاده از قوانین کیرشهف کاهش میدهد. در آموزش بعدی در مورد مدارهای DC، به تجزیه و تحلیل جریان مش برای انجام اینکار خواهیم پرداخت.