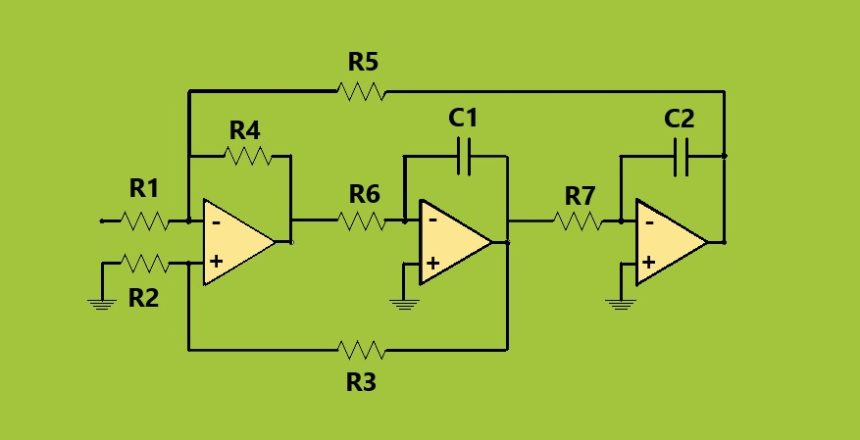
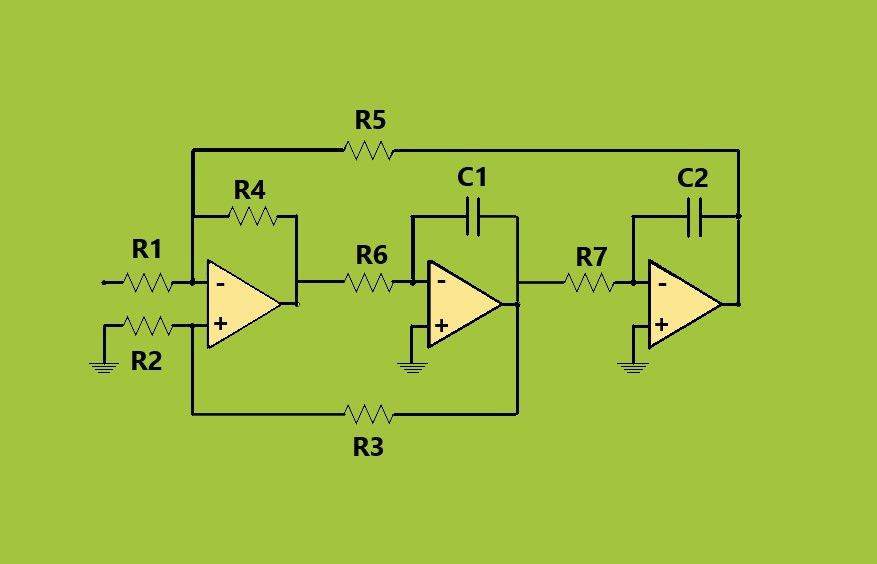
فیلترهای حالت متغیر از سه (یا بیشتر) مدار تقویتکننده عملیاتی کسکود شده (عنصر اکتیو) استفاده میکنند تا خروجیهای جداگانه فیلتر را تولید کنند، اما در صورت نیاز میتوان یک تقویتکننده جمعکننده اضافی نیز اضافه کرد تا پاسخ خروجی فیلتر چهارم یعنی فیلتر میاننگذر را نیز ایجاد کند.
فیلترهای حالت متغیر، فیلترهای اکتیو RC درجه دوم هستند که از دو تقویتکننده انتگرالگیر یکسان که هر کدام به عنوان یک فیلتر پایینگذر تک قطبی درجه اول عمل میکنند و از یک تقویتکننده جمعکننده که میتوانیم گین فیلترها و فیدبک میرایی شبکه را تنظیم کنیم، تشکیل شدهاند. سیگنالهای خروجی از هر سه طبقه تقویتکننده به ورودی باز میگردند و به ما اجازه میدهند حالتهای مختلف مدار را ایجاد کنیم.
یکی از مزایای اصلی طراحی فیلتر حالت متغیر این است که هر سه پارامتر اصلی فیلترها یعنی گین (A)، فرکانس گوشه (fC) و ضریب کیفیت فیلترها Q را میتوان به طور مستقل تنظیم کرد بدون اینکه بر عملکرد فیلترها تاثیر بگذارد.
در واقع اگر به درستی طراحی شود، نقطه فرکانس گوشه منفی 3 دسیبل برای هر دو پاسخ دامنه پایینگذر و پاسخ دامنه بالاگذر باید با نقطه فرکانس مرکزی طبقه میانگذر یکسان باشد. یعنی ƒLP(-3dB) برابر ƒHP(-3dB) که برابر ƒBP(center)است. همچنین ضریب میرایی (ζ) برای پاسخ فیلتر میانگذر باید برابر با باشد زیرا Q روی منفی 3 دسیبل (7071/0) تنظیم میشود.
اگرچه این نوع فیلتر، خروجیهای پایینگذر (LP)، بالاگذر (HP) و میانگذر (BP) را ارائه میدهد، کاربرد اصلی این نوع مدار فیلتر، به عنوان یک طرح فیلتر میانگذر حالت متغیر با فرکانس مرکزی تنظیم شده توسط دو انتگرالگیر RC است.
قبلا دیدهایم که ویژگیهای فیلترهای میانگذر را میتوان با کسکود کردن یک فیلتر پایینگذر با یک فیلتر بالاگذر بهدست آورد، فیلترهای میانگذر حالت متغیر این مزیت را دارند که میتوان آنها را به گونهای تنظیم کرد که انتخابکنندگی بالا (Q بالا) داشته باشند و در نقطه فرکانس مرکزی گین بالایی ارائه دهند.
چندین طرح فیلتر حالت متغیر وجود دارد که همگی بر اساس طراحی فیلتر استاندارد با تقویتکنندههای معکوس و غیرمعکوس موجود هستند. با این حال، طراحی اصلی فیلتر برای هر دو حالت، همانطور که در شکل زیر نشان داده شده است، یکسان خواهد بود.
دیاگرام فیلتر حالت متغیر
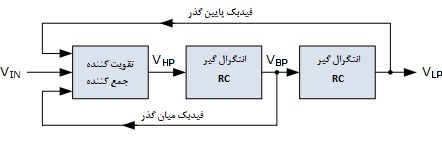
پس از دیاگرام اصلی بالا متوجه میشویم که فیلتر حالت متغیر دارای سه خروجی از هر کدام از 3 تقویتکننده با نامهای VHP، VBP و VLP است. پاسخ فیلتر میاننگذر را میتوان با اضافه کردن یک تقویتکننده چهارم نیز به دست آورد.
با یک ولتاژ ورودی ثابت Vin، خروجی از تقویتکننده جمعکننده یک پاسخ بالاگذر ایجاد میکند که همچنین به ورودی اولین انتگرالگیر RC تبدیل میشود. خروجی این انتگرالگیر یک پاسخ میانگذر تولید میکند که به ورودی دومین انتگرالگیر RC تبدیل میشود و خروجی آن پاسخ پایینگذر تولید میکند. در نتیجه، توابع انتقال جداگانه برای تکتک خروجیها را با توجه به ولتاژ ورودی میتوان یافت.
بنابراین طراحی اولیه فیلتر حالت متغیر غیرمعکوس به صورت زیر ارائه میشود:
مدار فیلتر حالت متغیر
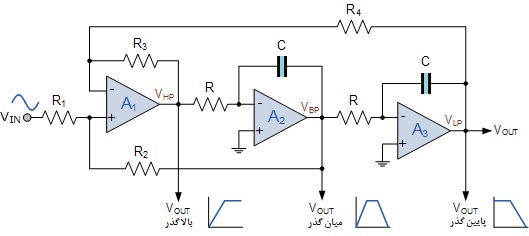
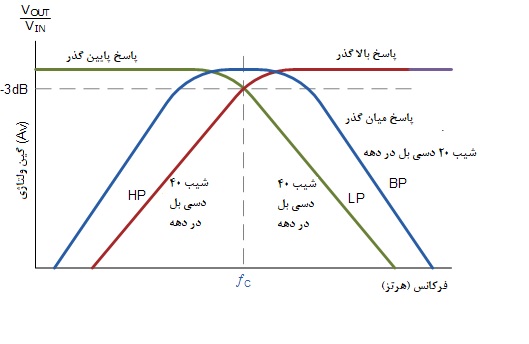
و پاسخ دامنه هر سه خروجی از فیلتر حالت متغیر به این صورت خواهد بود:
پاسخ نرمالیزه فیلتر حالت متغیر
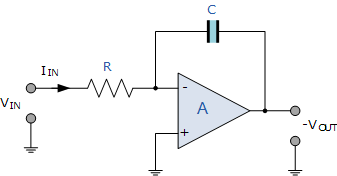
یکی از عناصر اصلی طراحی فیلتر حالت متغیر، استفاده آن از دو تقویتکننده انتگرالگیر است. همانطور که در آموزش انتگرالگیر دیدیم، تقویتکننده انتگرالگیر از یک امپدانس وابسته به فرکانس به شکل یک خازن در حلقه فیدبک خود استفاده میکند. به دلیل استفاده از یک خازن، ولتاژ خروجی متناسب با انتگرال ولتاژ ورودی است.
مدار تقویتکننده انتگرالگیر
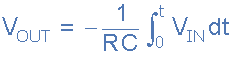
برای سادهسازی روابط ریاضی، فرمول بالا را میتوان در حوزه فرکانس به شکل زیر بازنویسی کرد:
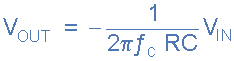
ولتاژ خروجی Vout برابر است با مقدار ثابت ضرب در انتگرال ولتاژ ورودی Vin نسبت به زمان. انتگرالگیرها یک تاخیر فاز با علامت منفی (-) ایجاد میکنند که نشاندهنده تغییر فاز 180 درجه است زیرا سیگنال ورودی مستقیما به پایه ورودی منفی تقویتکننده متصل است.
در مورد آپامپ A2 در بالا، سیگنال ورودی آن به خروجی آپامپ A1 متصل است، بنابراین ورودی A2 به عنوان VHP و خروجی آن به عنوان VBP نامگذاری شدهاست. پس از شکل بالا میتوان معادله تقویتکننده A2 را به صورت زیر نوشت:
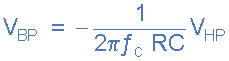
سپس با جابجایی برخی از پارامترها، میتوانیم تابع انتقال انتگرالگیر معکوسکننده A2 را به صورت زیر مشخص کنیم:
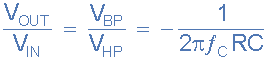
دقیقا همان فرض را میتوان انجام داد تا تابع انتقال انتگرالگیر دیگر A3 نیز مشخص شود:
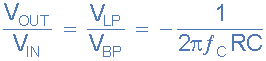
بنابراین دو تقویتکننده انتگرالگیر A2 و A3 به صورت کسکود به هم متصل میشوند تا خروجی اولی (VBP) به ورودی دومی تبدیل شود. بنابراین میبینیم که پاسخ میانگذر با انتگرالگیری از پاسخ بالاگذر و پاسخ پایینگذر با انتگرالگیری از پاسخ میانگذر ایجاد میشود. بنابراین تابع انتقال بین VHP و VLP به صورت زیر ارائه میشود:
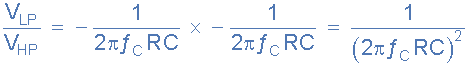
توجه داشته باشید که هر مرحله انتگرالگیری یک خروجی معکوس ارائه میدهد اما خروجی جمع مثبت خواهد بود زیرا آنها انتگرالگیرهای معکوسکننده هستند. اگر دقیقا از مقادیر یکسانی برای R و C استفاده شود تا دو مدار انتگرالگیر ثابت زمانی یکسانی داشته باشند، دو مدار تقویتکننده را میتوان به عنوان یک مدار انتگرالگیر تک با فرکانس گوشه fC در نظر گرفت.
فیلتر همچون دو مدار انتگرالگیر، دارای یک تقویت کننده جمعکننده دیفرانسیلی است که جمع وزنی ورودیها را در خروجی ایجاد میکند. مزیت در اینجا این است که ورودیهای تقویتکننده جمعکننده A1 پارامترهای فیدبک نوسانی، میرایی و سیگنال های ورودی را در داخل فیلتر جمع میکند زیرا هر سه خروجی به ورودیهای جمعکننده باز میگردند.
مدار تقویتکننده جمعکننده
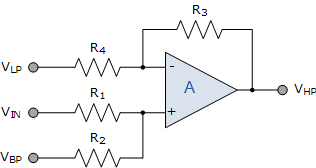
تقویتکننده عملیاتی A1 به صورت مدار جمعکننده/تفریقکننده بسته شدهاست. به عبارت دیگر، سیگنال ورودی Vin با خروجی آپامپ A2 یعنی VBP جمع شده و از این حاصل، مقدار خروجی آپامپ A3 یعنی VLP کم میشود.
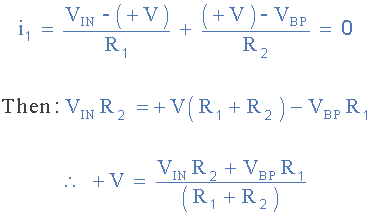
و در ادامه داریم:
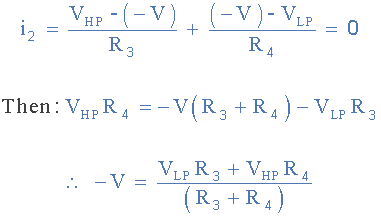
از آنجایی که ورودیهای دیفرانسیلی، +V و -V یک تقویتکننده عملیاتی یکسان هستند، یعنی +V = -V، میتوانیم دو عبارت بالا را دوباره مرتب کنیم تا تابع انتقال خروجی A1، خروجی بالاگذر را پیدا کنیم.
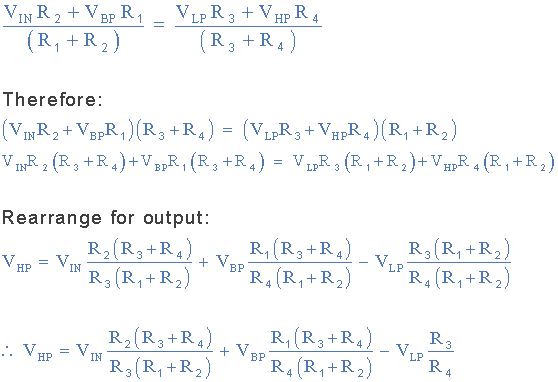
از بالا میدانیم که VBP و VLP خروجیهای دو انتگرالگیر A2 و A3 هستند. با جایگزینی معادلات انتگرالگیر برای A2 و A3 در معادله فوق، تابع انتقال فیلتر حالت متغیر را بدست میآوریم:
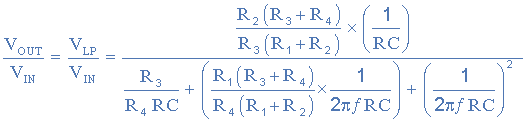
قبلا گفتیم که یک فیلتر حالت متغیر سه پاسخ فیلتر پایینگذر، بالاگذر و میانگذر ایجاد میکند و اینکه پاسخ میانگذر، یک فیلتر بسیار باریک با Q بالا است و این در تابع انتقال فیلتر حالت متغیر در بالا مشهود است زیرا شبیه به یک پاسخ درجه دوم استاندارد است.
تابع انتقال نرمالیزه درجه دوم
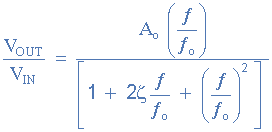
فرکانس گوشه فیلترها یا fC
فرکانس گوشه فیلتر حالت متغیر
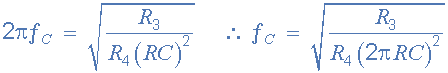
اگر فرض کنیم که مقاومتهای فیدبک R3 و R4 برابر هستند، پس فرکانس گوشه تمامی فیلترهای موجود در فیلتر حالت متغیر به شکل زیر خواهد بود:
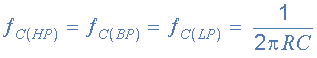
پس تنظیم فرکانس گوشه فیلتر حالت متغیر به سادگی با تغییر مقاومت تنظیم R یا خازن C انجام میشود.
فیلترهای حالت متغیر نه تنها با تکتک پاسخهای خروجی، بلکه با ضریب کیفیت فیلترها یا Q نیز مشخص میشوند. Q به «تیز بودن» منحنی پاسخ دامنه فیلترهای میانگذر مربوط میشود و هر چه Q بالاتر باشد، پاسخ خروجی تیزتر خواهد بود و در نتیجه فیلتری بسیار انتخابی ایجاد میشود.
برای فیلتر میانگذر، Q به عنوان فرکانس مرکزی تقسیم بر پهنای باند منفی 3 دسیبل فیلترها، یعنی به صورت Q=fC/BW تعریف میشود. اما Q را می توان از مخرج تابع انتقال فوق نیز یافت زیرا معکوس ضریب میرایی (ζ) است. پس Q به صورت زیر داده میشود:
ضریب کیفیت یا Q برای فیلتر حالت متغیر
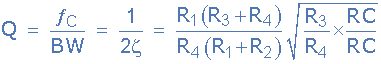
مجددا، اگر مقاومتهای R3 و R4 برابر باشند و هر دو مولفه انتگرالگیر R و C برابر باشند، عبارت ریشه دوم نهایی به 1√ یا به 1 منتهی میشود زیرا صورت و مخرج یکدیگر را خنثی میکنند.
مثال 1- فیلتر حالت متغیر
یک فیلتر حالت متغیر طراحی کنید که دارای فرکانس گوشه fC (طبیعی بدون میرایی)، 1 کیلوهرتز و ضریب کیفیت یا Q برابر 10 باشد. فرض کنید مقاومتها و خازنهای تعیینکننده فرکانس برابر هستند. گین DC فیلترها را تعیین کنید و مدار حاصل و نمودار بد را رسم کنید.
ما در بالا گفتیم که اگر هر دو مقاومت R و خازن فیدبک C دو مدار انتگرالگیر مقادیر یکسانی داشته باشند، یعنی R = R و C = C، نقطه قطع یا فرکانس گوشه برای فیلتر به سادگی به این صورت خواهد بود:
فرکانس گوشه فیلتر
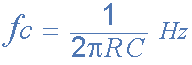
میتوانیم یکی از دو المان مقاومت یا خازن را به دلخواه به صورت منطقی انتخاب کنیم تا مقدار دیگری بر حسب فرمول محاسبه شود. اگر فرض کنیم که مقدار خازن به صورت منطقی برابر با 10 نانوفاراد است، مقدار مقاومت برابر خواهد بود با:
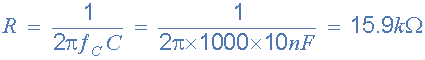
پس مقدار خازن برابر با 10 نانوفاراد و مقدار مقاومت برابر با 9/15 کیلواهم یا 16 کیلواهم در نزدیکترین حالت خواهند بود.
مقدار Q برابر با 10 است. پس ضریب میرایی فیلتر به این شکل خواهد بود:
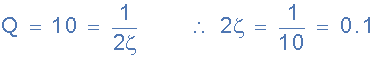
در تابع انتقال فیلتر حالت متغیر بالا، اگر به جای 2ζ از ترکیب مقاومتها استفاده کنیم، خواهیم داشت:
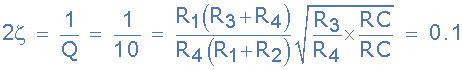
میدانیم که مقاومت R برابر با 16 کیلواهم و خازن C برابر با 10 نانوفاراد است. اگر فرض کنیم که مقاومتهای فیدبک یعنی R3 و R4 مقادیر یکسانی برابر با 10 کیلواهم دارند، در این صورت معادله بالا به شکل زیر خواهد شد:
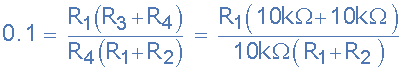
اگر یک مقدار مناسب مثلا 1 کیلواهم برای مقاومت R1 فرض کنیم، مقدار مقاومت R2 را میتوانیم به این صورت بیابیم:
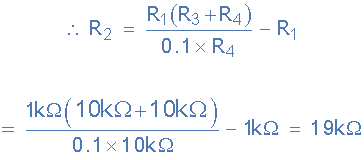
گین DC باند عبور در تابع انتقال نرمالیزه A0 است و با توجه به تابع انتقال فیلتر حالت متغیر، مقدار آن برابر است با:
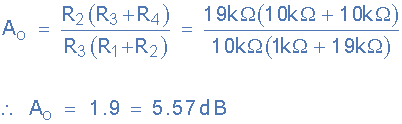
پس گین DC فیلتر برابر با 9/1 که برابر با است محاسبه شد. همچنین حداکثر گین فیلتر در نقطه fC را میتوان با حاصلضرب Q در A0 یافت:
حداکثر گین فیلتر حالت متغیر
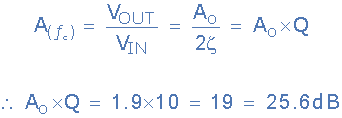
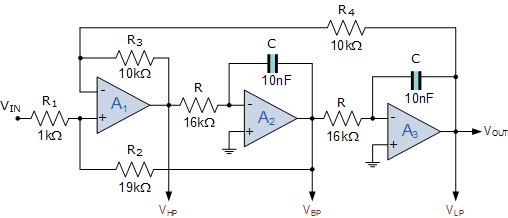
مدار فیلتر حالت متغیر
پس المانهای مدار فیلتر حالت متغیر مثال اول به این صورت خواهد بود:
R = 16kΩ, C = 10nF, R1 = 1kΩ,
R2 = 19kΩ and R3 = R4 = 10kΩ
طرح فیلتر حالت متغیر
حال میتوانیم منحنی پاسخ تکتک خروجیها را برای مدار فیلتر حالت متغیر در محدوده فرکانسی بین 1 هرتز تا 1 مگاهرتز به صورت نمودار بد زیر رسم کنیم.
نمودار بد (Bode) فیلتر حالت متغیر
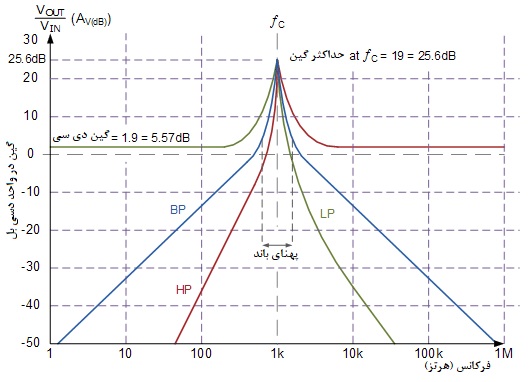
پس از منحنیهای پاسخ فیلترها در بالا میبینیم که گین DC مدار فیلتر 57/5 دسیبل است و همانطور که در بالا محاسبه شد برابر است با گین ولتاژی حلقه باز، Ao یا 9/1. پاسخ همچنین نشان میدهد که منحنیهای خروجی به دلیل مقدار Q با حداکثر گین ولتاژی 6/25دسیبل در فرکانس گوشه به اوج میرسند.
همانطور که میدانیم مقدار Q فرکانس مرکزی فیلترهای میانگذر را نیز به پهنای باند آن مرتبط میکند، بنابراین پهنای باند فیلتر برابر با خواهد بود.
در این مقاله فیلتر حالت متغیر دیدیم که به جای اینکه یک فیلتر اکتیو یک نوع پاسخ فرکانسی تولید کند، میتوانیم از تکنیکهای چند فیدبکه برای تولید هر سه پاسخ فیلتر، پایینگذر، بالاگذر و میانگذر به طور همزمان از تنها یک فیلتر اکتیو استفاده کنیم.
اما علاوه بر سه پاسخ فیلتر اصلی، میتوانیم یک مدار تقویتکننده اضافی را به طرح فیلتر حالت متغیر پایه در بالا اضافه کنیم تا یک پاسخ خروجی چهارم شبیه به یک فیلتر میاننگذر استاندارد تولید کنیم.
طراحی فیلتر میان نگذر
فیلتر ناچ اساسا مخالف فیلتر میانگذر است، به این معنا که اجازه عبور یک باند فرکانس خاصی را نمیدهد. یک فیلتر ناچ به عنوان «فیلتر میاننگذر» نیز شناخته میشود. برای به دست آوردن پاسخ یک فیلتر میاننگذر از طراحی فیلتر حالت متغیر پایه، باید پاسخهای خروجی بالاگذر و پایینگذر را با استفاده از یک تقویتکننده جمعکننده دیگر، A4، با هم جمع کنیم.
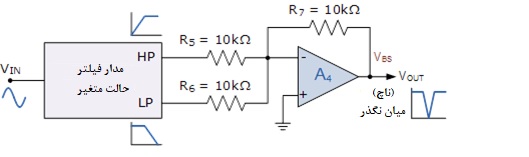
در اینجا برای سادهسازی فرض کردهایم که دو مقاومت ورودی، R5 و R6 و همچنین مقاومت فیدبک، R7 همگی همچون R3 و R4 مقدار 10 کیلواهم دارند. بنابراین فیلتر میاننگذر گین 1 یا واحد خواهد داشت.
پاسخ خروجی فیلتر میاننگذر و فیلتر میانگذر به یکدیگر مرتبط هستند به این صورت که فرکانس مرکزی پاسخ فیلتر میانگذر برابر با نقطه صفر پاسخ فیلتر میاننگذر است و در این مثال 1 کیلوهرتز خواهد بود.
همچنین پهنای باند فیلتر میاننگذر دقیقا همچون فیلتر میانگذر توسط Q مدار مشخص میشود. بنابراین پیک رو به پایین برابر است با فرکانس مرکزی تقسیم بر پهنای باند منفی 3 دسیبل، یعنی اختلاف فرکانس بین نقاط منفی 3 دسیبل در دو طرف فیلتر میاننگذر. توجه داشته باشید که ضریب کیفیت Q ربطی به عمق واقعی فیلتر میاننگذر ندارد.
این طرح فیلتر میاننگذر پایه، تنها دو ورودی به تقویتکننده جمعکننده خود دارد، خروجی پایینگذر VLP و خروجی بالاگذر VHP. با این حال، دو سیگنال دیگر برای استفاده از مدار فیلتر حالت متغیر اولیه، خروجی میانگذر، VBP و خود سیگنال ورودی، VIN وجود دارد.
اگر یکی از این دو سیگنال به عنوان ورودی تقویتکننده جمعکننده فیلتر میاننگذر همراه با سیگنالهای پایینگذر و بالاگذر نیز استفاده شود، میتوان عمق فیلتر میاننگذر را کنترل کرد.
اینکه چگونه می خواهید خروجی فیلتر میاننگذر را کنترل کنید، بستگی به این دارد که از کدام یک از دو سیگنال موجود استفاده کنید. اگر لازم بود که خروجی میاننگذر از یک پاسخ منفی به یک پاسخ مثبت در فرکانس طبیعی نامیرا fO تغییر کند، از سیگنال خروجی میانگذر VBP استفاده میشود.
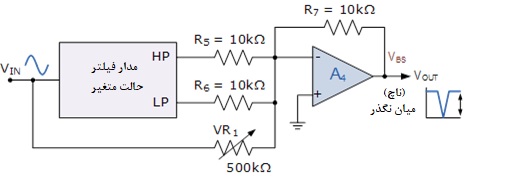
به همین ترتیب، اگر لازم بود که خروجی فیلتر میاننگذر فقط در عمق منفی رو به پایین آن تغییر کند، از سیگنال ورودی VIN استفاده میشود. اگر یکی از این دو سیگنال اضافی از طریق یک مقاومت متغیر به تقویتکننده جمعکننده متصل شود، عمق و جهت خروجی میاننگذر را میتوان به طور کامل کنترل کرد. مدار فیلتر میاننگذر اصلاح شده زیر را در نظر بگیرید.
عمق فیلتر میاننگذر متغیر
خلاصه فیلتر حالت متغیر
مدار فیلتر حالت متغیر، (SVF) یک طرح فیلتر RC اکتیو درجه دوم است که از تکنیکهای چند فیدبکه برای تولید سه خروجی پاسخ فرکانسی مختلف یعنی پایینگذر، بالاگذر و میانگذر از یک فیلتر واحد استفاده میکند. مزیت فیلتر حالت متغیر نسبت به سایر طرحهای فیلتر اصلی این است که سه پارامتر اصلی فیلتر یعنی گین، ضریب کیفیت و فرکانس گوشه را میتوان به طور مستقل تنظیم کرد.
همچنین تنظیم کردن فیلتر نیز آسان است زیرا فرکانس گوشه را میتوان با تغییر R یا C بدون تاثیر بر ضریب میرایی فیلتر تنظیم کرد. با این حال، در فرکانسهای گوشهای بالاتر و ضریبهای میرایی بزرگتر، فیلتر میتواند ناپایدار شود، بنابراین بهتر است با Q پایین، کمتر از 10، و در فرکانسهای گوشه پایین استفاده شود.
طراحی فیلتر حالت متغیر پایه از سه بخش تقویتکننده برای تولید خروجیهای خود استفاده میکند، اما با افزودن چهارمین تقویتکننده که خروجی های سیگنالهای پایینگذر و بالاگذر را با هم جمع میکند، یک پاسخ خروجی ناچ یا میاننگذر نیز میتواند در فرکانس مرکزی دلخواه به دست آید.