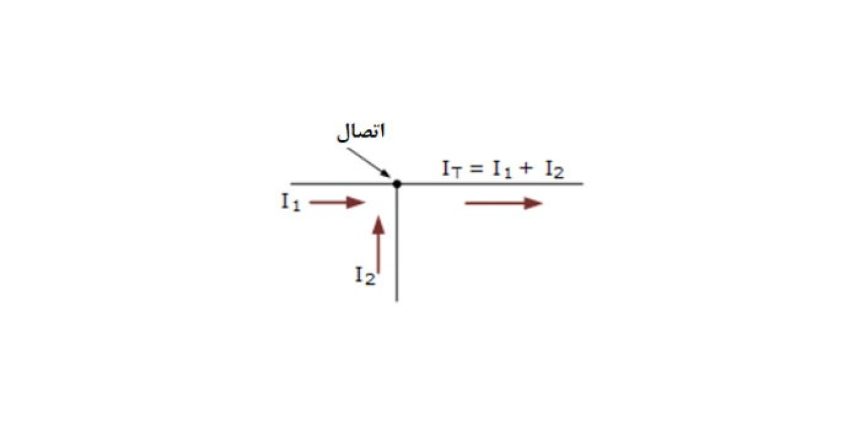
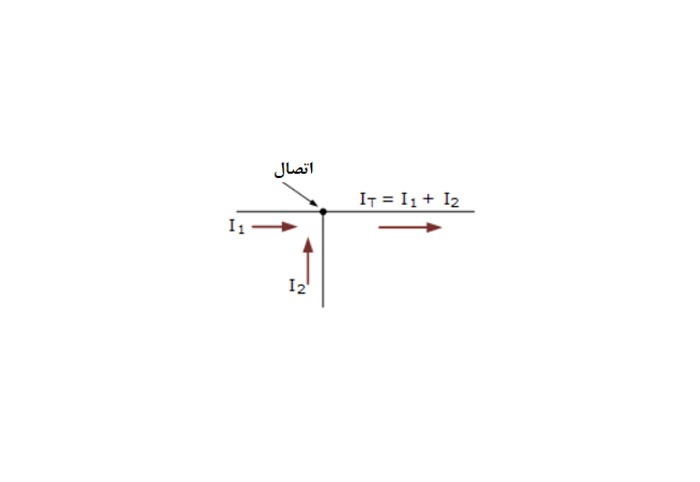
قانون جریان کیرشهف (KCL)، اولین قانونی است؛ که با بقای شارژ ورودی و خروجی یک اتصال، سروکار دارد.
برای تعیینکردن مقدار یا بزرگی جریان الکتریکی جاری، در یک مدار الکتریکی یا الکترونیکی، نیاز به استفاده از قوانین خاصی داریم؛ که به ما اجازهی نوشتن این جریانات در قالب یک معادله را بدهد. شبکهی معادلات استفادهشده براساس قوانین کیرشهف بوده و از آنجایی که با جریانهای مدار سروکار داریم؛نگاهی بر قانون جریان کیرشهف (KCL) خواهیم داشت.
قانون جریان گوستاو کیرشهف،از اولین قانونهای اساسی است؛ که برای تجزیهوتحلیل مدار استفاده میشود. قانون جریان وی، بیان میکند؛ که برای یک مسیر موازی، کل جریان ورودی به یک اتصال مدار،دقیقا برابر با کل جریان خروجی از آن اتصال است. زیرا به دلیل از بین نرفتن شارژ، هیچ راه دیگری برای جریان نیست.
به بیان دیگر، جمع جبری تمام جریانهای ورودی و خروجی اتصال باید برابر با صفر باشد. (Σ IIN = Σ IOUT)
این ایده توسط کیرشهف را، معمولا بهصورت بقای بار میشناسند؛ زیرا جریان در اتصال، بدون از دسترفتن، حفظ میشود. بیایید نگاهی به مثال سادهای از قانون جریان کیرشهف (KCL) هنگامیکه به یک اتصال منفرد اعمال میشود؛ داشتهباشیم.
یک اتصال منفرد
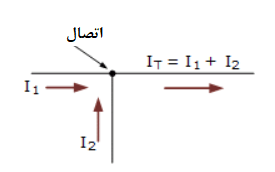
در این مثال سادهی اتصال منفرد، در اینجا، جریان IT که از اتصال خارج میشود؛ برابر با جمع جبری I1 + I2 بوده، که به اتصال وارد میشوند و درنتیجه: IT = I1 + I2 خواهد بود. همچنین میتوان آن را بهصورت جمع جبری IT – (I1 + I2) = 0 نیز نوشت.
پس اگر I1 برابر با ۳ آمپر و I2 نیز برابر با ۲ آمپر باشد؛ درنتیجه، جریان کل IT که از اتصال خارج میشود برابر با ۵=۳+۲ خواهدبود و میتوانیم از این قانون پایه، برای هر تعداد اتصال یا گرهای، از آنجایی که مجموع جریان های ورودی و خروجی، باهم برابر خواهدبود؛ استفاده نماییم.
همچنین، حتی اگر جهت جریانها را برعکس کنیم؛ معادلات نهایی همچنان برای I۱ و I2 صادق خواهد بود. زیرا I1 = IT – I2 = 5 – 2 = 3 آمپر و I2 = IT – I1 = 5 – 3 = 2 آمپر است. پس میتوانیم فرضکنیم که جریانات ورودی به اتصال مثبت(+) بوده؛ درحالیکه، جریانات خروجی از آن(-) است.
پس میتوان دید که جمع ریاضیاتی جریانها، چه ورودی به اتصال و چه خروجی از آن، درهر جهتی، همیشه برابر با صفر، خواهدبود و این امر، پایهی قانون اتصال کیرشهف، یا قانون بیشتر شناختهشدهی جریان کیرشهف یا (KCL) را شکل میدهد.
مقاومت های موازی
بیایید نگاه کنیم؛ که چگونه میتوان قانون جریان کیرشهف را به مقاومتهای موازی، با مقادیر مقاومتی برابر یا نابرابر اعمال نمود. نمودار مداری زیر را در نظر بگیرید:
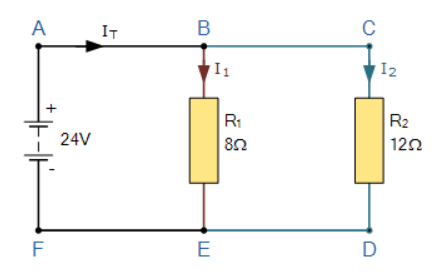
در این مثال ساده مقاومت موازی، دو اتصال مجزا برای جریان وجود دارد؛ که یک اتصال در گرهی B و یک اتصال در گرهی E میباشد. بنابراین، میتوانیم از قانون اتصال کیرشهف، برای جریانهای الکتریکی در هردوی این اتصالات مجزا و جریانهای ورودی به اتصال و خروجی از آن، استفاده کنیم.
برای شروع، تمام جریان IT، از منبع ۲۴ ولتی خارجشده و به نقطهی A رسیده و پس از به گره B وارد میشود. گره B، یک اتصال است؛ زیرا جریان میتواند در آن به دو جهت مجزا تقسیم شود. مقداری از جریان، به پایین و از طریق مقاومت R1 جاری میشود؛ درحالیکه که مابقی آن از طریق گره C به مقاومت R2 میرسد. توجه داشته باشید؛ که جریانهای ورودی و خروجی از یک نقطهی گره، معمولا جریانهای شاخهای، نامیده میشوند.
میتوانیم از قانون اهم، برای تعیین جریانهای شاخهای منحصربفرد از طریق هر مقاومت استفاده کنیم ( I = V/R).
برای جریان شاخهی B به E از طریق مقاومت R1:
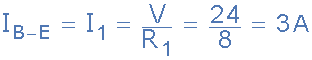
برای جریان شاخهی C به D از طریق مقاومت R2:
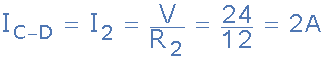
از بالا میدانیم؛ که قانون جریان کیرشهف، بیان میدارد، که مجموع جریانهای ورودی به یک اتصال باید برابر با مجموع جریانهای خروجی از آن باشد و در مثال سادهی بالا، یک جریان IT به اتصال گره B، وارد میشود و دو جریان I1 و I2 از اتصال خارج میگردند.
از آنجایی که از محاسبات میدانیم؛ که جریانهای خروجی از اتصال گره B، I1 برابر با ۳ آمپر و I2 برابر با ۲ آمپر است، درنتیجه، مجموع جریانهای ورودی به اتصال در گره B باید برابر با مجموع دو جریان ۵=۲+۳ باشد. پس ΣIN = IT = 5 است.
در مثال ما، دو اتصال مجزا در گره B و گره E وجود دارد و بنابراین، از طریق دیگری نیز، میتوان مقدار جریان IT را تایید نمود؛ زیرا دو جریان، درگره E نیز، دوباره با یکدیگر ترکیب میشوند. بنابراین، برای اینکه، قانون اتصال کیرشهف، صادق باشد؛ باید مجموع جریانهای ورودی نقطهی F ،برابر با مجموع جریانهای خروجی از اتصال در گره E باشد.
از آنجایی که، دو جریان ورودی به اتصال E، بهترتیب برابر با ۳ و ۲ آمپر است؛ مجموع جریانهای ورودی نقطهی F نیز برابر با ۵=۲+۳ آمپر است. پس ΣIN = IT = 5 و بنابراین، قانون جریان کیرشهف، از آنجایی که همین مقدار از نقطه A خارج میشود؛ صادق است.
اعمال KCL به مدار های پیچیده تر
میتوانیم، از قانون جریان کیرشهف، برای یافتن جریانهای جاری در مدارهای پیچیدهتر استفاده کنیم. تاکنون میدانیم؛ که جمع جبری تمام جریانهای یک گره (نقطهی اتصال) برابر با صفر است و با داشتن این ایده در ذهن، تعیین جریانهای ورودی به یک گره و نیز خروجی از آن، کار سادهای خواهد بود. مدار زیر را در نظر بگیرید:
مثال شماره 1 قانون جریان کیرشهف
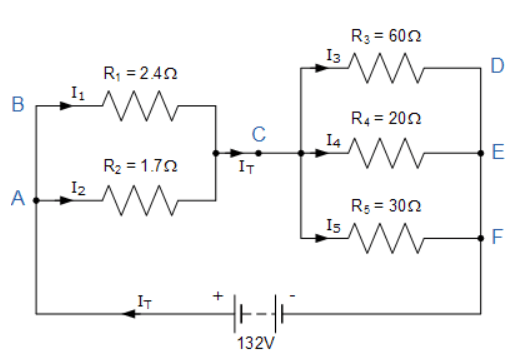
در این مثال، چهار اتصال مجزا برای جداسازی یا ادغام جریان درگرههای A، C،E و F وجود دارد. جریان منبع IT درگره A جداشده و از طریق مقاومتهای R1 و R2 جریان مییابد، سپس دوباره در گره C ، قبل از دوباره جاری شدن از طریق مقاومتهای R3، R4 و R5 ترکیب شده و درنهایت، یکبار دیگر در گره F باهم ترکیب میشوند.
اما پیش از محاسبهی جریانهای منحصربفرد جاری در هر شاخهی مقاومت، ابتدا باید جریان کلی مدار یعنی IT را محاسبه کرد. قانون اهم به ما میگوید؛ و از آنجایی که میدانیم مقدار V برابر با ۱۳۲ ولت است؛ نیاز داریم که مقادیر مقاومتی مدار را بهصورت زیر بیابیم:
مقدار مقاومتی مدار Rac
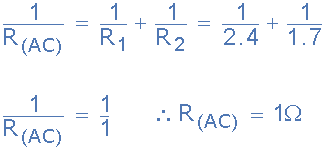
بنابراین ، مقدار مقاومتی معادل مدار، بین گرههای A و C ، برابر با ۱ اهم، محاسبه شدهاست.
مقدار مقاومتی مدار Rcf
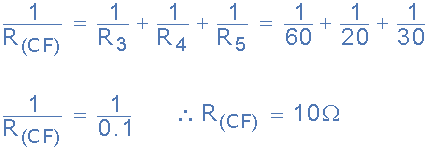
بنابراین ، مقدار مقاومتی معادل مدار، بین گرههای C و F ، برابر با ۱۰ اهم محاسبه شدهاست. پس جریان کل مدار IT بهصورت زیر خواهدبود:
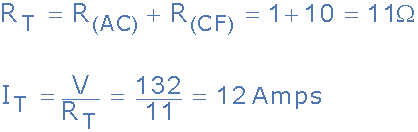
درنهایت، معادل مدار خواهد بود:
مدار معادل قانون جریان کیرشهف
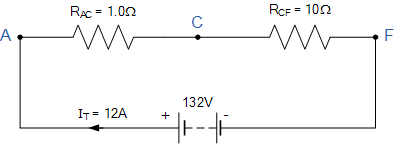
از اینرو، V = 132V،RAC = 1Ω ،RCF = 10Ω و IT = 12A خواهد بود.
با ایجاد مقادیر مقاومتی موازی معادل و منبع جریان، اکنون میتوانیم جریانهای شاخهای منحصربفرد را محاسبه نموده و استفاده از قانون اتصال کیرشهف را بهصورت زیر تایید کنیم

از اینرو I1 = 5A ،I2 = 7A ،I3 = 2A, I4 = 6A و I5 = 4A خواهد بود.
میتوانیم با استفاده از گره C بهعنوان نقطهی مرجع خود، جریانات ورودی و خروجی به اتصال را بهصورت زیر بیابیم و تایید کنیم که قانون جریان کیرشهف در مدار صادق است.
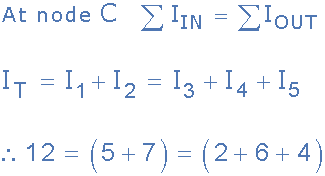
میتوانیم دوباره چک کنیم تا ببینیم که آیا قانون اتصال کیرشهف، زمانیکه جریانهای ورودی به اتصال مثبت و جریانهای خروجی از آن منفی است؛ صادق است؟! پس جمع جبری I1 + I2 – I3 – I4 – I5 = ۰ است که برابر با ۰ = ۵ + ۷ – ۲ – ۶ – ۴ خواهدبود.
پس ما میتوانیم با تجزیهوتحلیل تایید کنیم؛ که، قانون جریان کیرشهف (KCL) بیان میکند: جمع جبری جریانها، در یک نقطهی اتصال در یک شبکهی مداری برابر با صفر است، در این مثال درست و صحیح است.
مثال شماره 2 قانون جریان کیرشهف
جریانهای جاری در مدار زیر را، تنها توسط قانون جریان کیرشهف بیابید.
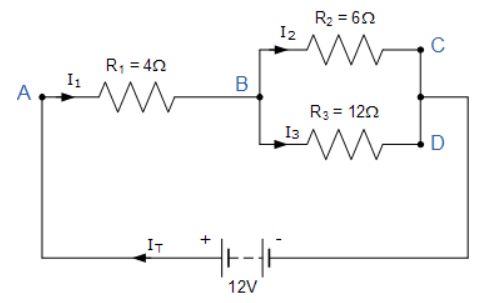
IT، جریان کلی جاری در مدار است؛ که توسط منبع ولتاژ ۱۲ ولت رانده میشود. درنقطهی A، جریان I۱ برابر با IT بوده و بنابراین، افت ولتاژ I1*R را در دوسر مقاومت R1 خواهیم داشت.
مدار دارای 2 شاخه، 3 گره ( B ، C و D) و 2 حلقهی مستقل است و درنتیجه، افت ولتاژ در حلقهها خواهدبود:
- حلقه ABC ⇒ ۱۲ = ۴I1 + ۶I2
- حلقه ABD ⇒ ۱۲ = ۴I1 + ۱۲I3
از آنجاییکه، قانون جریان کیرشهف بیان میکند؛ در گره B، معادله I1 = I2 + I3 برقرار خواهد بود و بنابراین میتوانیم I1 را جایگزین I2 + I3 در هر دو معادلهی حلقهی زیر کرده و سپس ساده کنیم.
معادلات حلقه کیرشهف
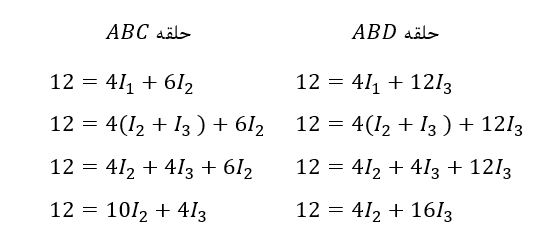
ما درحال حاضر، دومعادلهی همزمان داریم؛ که مربوط به جریانهای جاری در مدار است.
معادله شماره ۱ : 12 = 10I2 + 4I3
معادله شماره ۲ : 12 = 4I2 + 16I3
با ضرب معادلهی اول (حلقهی ABC) در ۴ و سپس کم کردن حلقهی ABD از ABC، میتوانیم معادلات را کاهش دهیم تا مقادیر I2 و I3 را بیابیم.
معادله شماره ۱ : 12 = 10I2 + 4I3 ( x4 ) و 48 = 40I2 + 16I3
معادله شماره ۲ : 12 = 4I2 + 16I3 ( x1 ) و 12 = 4I2 + 16I3
معادله شماره ۱ – معادله شماره ۲ : 36 = 36I2 + 0
جایگزینی I2 برحسب I3، مقدار I2 را برابر با ۱ آمپر، نشان میدهد.
اکنون میتوانیم همین روند را برای یافتن مقدار I3، با ضرب معادلهی اول (حلقهی ABC) در ۴ و معادلهی دوم (حلقهی ABD) در ۱۰ انجام دهیم؛ سپس با کم کردن حلقهی ABC از ABD، میتوانیم معادلات را کاهش دهیم تا مقادیر I2 و I3 را بیابیم.
معادله شماره ۱ : 12 = 10I2 + 4I3 ( x4 ) و 48 = 40I2 + 16I3
معادله شماره ۲ : 12 = 4I2 + 16I3 ( x10 ) و 12 = 4I2 + 16I3
معادله شماره ۲ – معادله شماره ۱ : 72 = 144I3 + 0
جایگزینی I3 برحسب I2، مقدار I3 را برابر با ۰/۵ آمپر، نشان میدهد.
از آنجاییکه، قانون اتصال کیرشهف بیان میکند: I1 = I2 + I3
جریان منبع جاری در مقاومت R1 برابر با ۱/۰ + ۰/۵ = ۱/۵ خواهدبود.
بنابراین I1 = IT = ۱/۵ A ، I2 = 1/0 A و I3 = ۰/۵ A بوده و با این اطلاعات میتوان افت ولتاژ I*R را در هر دستگاه و نقاط مختلف(گره) اطراف مدار محاسبه کرد.
ما میتوانستیم مدار مثال 2 را، به سادگی و آسانی توسط قانون اهم حل کنیم؛ اما از قانون جریان کیرشهف در اینجا، استفاده کردیم تا نشان دهیم؛ استفاده از این قانون برای مدارهای پیچیدهتر، هنگامیکه استفاده از قانون اهم بهسادگی کاربرد ندارد؛ امکانپذیر است.