همه سیمپیچها، سلفها، چوکها و ترانسفورماتورها یک میدان مغناطیسی در اطراف خود ایجاد میکنند که شامل یک سلف سری با مقاومتی است که مدار سری LR را تشکیل میدهد.
اولین مقاله در این بخش در مورد سلفها، به طور خلاصه به ثابت زمانی یک سلف پرداختیم که بیان میکرد جریانی که از یک سلف میگذرد، نمیتواند به طور لحظهای تغییر کند، اما با نرخ ثابتی که توسط نیروی محرکه خودالقاشده در سلف تعیین میشود، افزایش مییابد.
به عبارت دیگر، یک سلف در مدار الکتریکی با عبور جریان (i) از داخلش مخالفت میکند. در حالی که این کاملا صحیح است، ما در آموزش این فرض را مطرح کردیم که یک سلف ایدهآل داریم که هیچ مقاومت یا خازن پارازیتی مرتبط با سیمپیچ وجود ندارد.
با این حال، در دنیای واقعی، «همه» سیمپیچها از قبیل چوک، سلونویید، رله یا هر المان سیمپیچیشدهای، در هر اندازهای که باشند، چه بزرگ چه کوچک، همیشه مقدار معینی مقاومت دارند. این امر به این خاطر است که سیمپیچهای واقعی سیم که برای ساخت آن استفاده میشود از سیم مسی استفاده میکند که دارای مقداری مقاومت است.
پس برای کاربردهای دنیای واقعی میتوانیم سیمپیچ ساده خود را به عنوان یک اتصال سری «اندوکتانس» و «مقاومت» یا به عبارت دیگر تشکیل یک مدار سری LR در نظر بگیریم.
مدار سری LR اساسا از یک سلف با اندوکتانس L به صورت سری با مقدار مقاومت R تشکیل شده است. مقاومت R مقدار مقاومتی DC حلقههای سیم است که برای تشکیل سیمپیچ سلف به کار رفته است. مدار سری LR زیر را در نظر بگیرید:
مدار اتصال سری LR
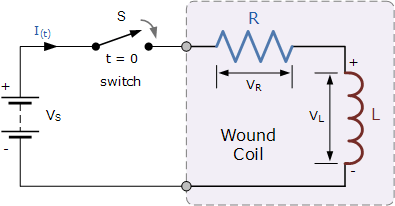
مدار سری LR فوق به دوسر یک منبع ولتاژ ثابت (باتری) و یک کلید متصل است. فرض کنید کلید S باز است تا زمانی که در زمان t = 0 بسته شود، و سپس برای همیشه بسته میماند و یک ورودی ولتاژ از نوع «پاسخ پله» تولید میکند. جریان i شروع به عبور از مدار میکند اما به سرعت به حداکثر مقدار Imax که با نسبت V / R (قانون اهم) تعیین می شود افزایش نمی یابد.
عامل محدودکننده نیروی محرکه خودالقاشده در سلف در نتیجه رشد شار مغناطیسی است (قانون لنز). پس از مدتی منبع ولتاژ اثر نیروی محرکه خودالقاشده را خنثی میکند، میزان عبور جریان ثابت میشود و در نتیجه جریان و میدان القایی به صفر میرسد.
میتوانیم از قانون ولتاژ کیرشهف (KVL) برای تعریف افت ولتاژ تکتک اجزای موجود مدار استفاده کنیم و سپس از آن برای بیان عبور جریان استفاده کنیم.
قانون ولتاژ کرشهف (KVL) به ما میدهد:
افت ولتاژ روی مقاومت R بر اساس قانون اهم رابر است با:
افت ولتاژ سلف با توجه به فرمول آشنای زیر به دست میآید:
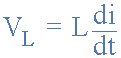
پس عبارت نهایی برای افت ولتاژ تکتک اجزای موجود در مدار سری LR به صورت زیر بیان میشود:

میبینیم که افت ولتاژ در مقاومت به جریان i بستگی دارد، در حالی که افت ولتاژ در سراسر سلف به نرخ تغییر جریان، di/dt بستگی دارد. هنگامی که جریان برابر با صفر است، (i = 0) در زمان t = 0 عبارت فوق، که همچنین یک معادله دیفرانسیل مرتبه اول است، میتواند بازنویسی شود تا مقدار جریان در هر لحظه از زمان به صورت زیر بشود:
عبارت جریانی برای مدار سری LR
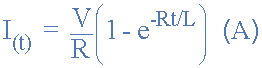
در این فرمول پارامترها به شکل زیر تعریف می شوند:
- V با واحد ولت
- R با واحد اهم
- L با واحد هانری
- T با واحد ثانیه
- e همان پایه لگاریتم طبیعی برابر با 71828/2
ثابت زمانی ( τ ) مدار سری LR به صورت L/R داده می شود و در آن V/R مقدار حالت پایدار نهایی را پس از پنج مقدار ثابت زمانی نشان میدهد. هنگامی که جریان به حداکثر مقدار حالت پایدار در برسد، اندوکتانس سیمپیچ به صفر رسیده و بیشتر شبیه یک اتصال کوتاه عمل میکند و عملا از مدار حذف میشود.
بنابراین جریان عبوری از سیمپیچ، فقط توسط عنصر مقاومتی با واحد اهم سیمپیچها محدود میشود. یک نمایش گرافیکی از رشد جریان که نشاندهنده ویژگیهای ولتاژ/زمان مدار است، میتواند به صورت زیر ارائه شود.
منحنی حالت گذرا برای اتصال سری LR
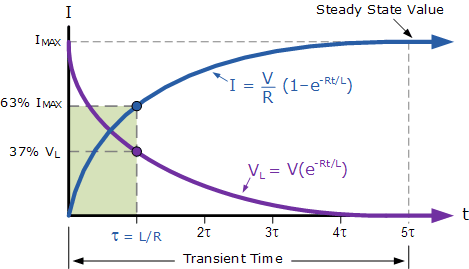
از آنجایی که افت ولتاژ در مقاومت VR برابر با I*R (قانون اهم) است، رشد و شکل نمایی مشابه جریان را خواهد داشت. با این حال، افت ولتاژ در سراسر سلف VL مقداری برابر با Ve(-Rt/L) خواهد داشت. پس ولتاژ در سرتاسر سلف VL مقدار اولیهای برابر با مقدار ولتاژ باتری در زمان t = 0 یا زمانی که کلید ابتدا بسته میشود و سپس به صورت نمایی به صفر میرسد، همانطور که در منحنی های بالا نشان داده شدهاست، خواهد داشت.
زمان لازم برای رسیدن مقدار جریان در مدار سری LR به حداکثر مقدار حالت پایدار خود معادل حدود 5 ثابت زمانی یا است. این ثابت زمانی τ با τ = L/R بر حسب ثانیه اندازهگیری میشود که R مقدار مقاومت بر حسب اهم و L مقدار سلف در واحد هانری است. پس یک مدار پایه شارژ RL تشکیل میشود که را میتوان به عنوان یا زمان گذرا مدار نیز در نظر گرفت.
زمان گذرا هر مدار القایی با رابطه بین اندوکتانس و مقاومت تعیین میشود. به عنوان مثال، برای یک مقاومت مقدار ثابت، هرچه اندوکتانس بزرگتر باشد، زمان گذرا کندتر خواهد بود و بنابراین ثابت زمانی طولانیتر برای مدار سری LR خواهد بود. به همین ترتیب، برای یک اندوکتانس با مقدار ثابت، هر چه مقدار مقاومت کمتر باشد، زمان گذرا طولانیتر میشود.
با این حال، برای یک اندوکتانس با مقدار ثابت، با افزایش مقدار مقاومت، زمان گذرا و در نتیجه ثابت زمانی مدار کوتاهتر میشود. این به این دلیل است که با افزایش مقاومت، مدار بیشتر و بیشتر مقاومت میکند زیرا مقدار اندوکتانس در مقایسه با مقاومت ناچیز میشود. اگر مقدار مقاومت به اندازه کافی در مقایسه با اندوکتانس افزایش یابد، زمان گذرا به طور موثر تقریبا به صفر کاهش مییابد.
مثال 1- اتصال سری LR
یک سیمپیچ که دارای اندوکتانس 40 میلیهانری است با یک مقاومت با مقدار 2 اهم به یکدیگر متصل شدهاند تا اتصال سری LR تشکیل شود. اگر به منلع ولتاژ 20 ولت متصل شوند.
الف) مقدار نهایی جریان را بیابید.
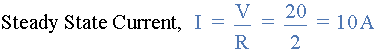
ب) ثابت زمانی مدار اتصال سری LR چه خواهد بود
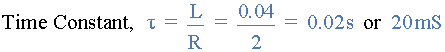
ج) مقدار زمان گذرای مدار اتصال سری LR چه خواهد بود
د) مقدار نیروی محرکه خودالقاشده پس از گذشت 10 میلیثانیه چقدر خواهد بود
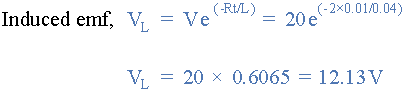
ه) مقدار جریان عبوری پس از گذشت یک ثابت زمانی و بسته شدن کلید چقدر است
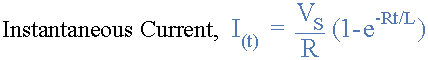
با توجه به ثابت زمانی مدار که برابر با 20 میلی ثانیه در قسمت ب محاسبه شده است، مقدار جریان پس از گذشت یک ثابت زمانی برابر خواهد بود با:
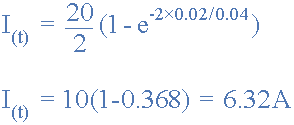
ممکن است متوجه شده باشید که پاسخ سوال ه که مقدار 32/6 آمپر را در زمان یک ثبات زمانی نشان میدهد، برابر با 2/63% مقدار جریان پایدار نهایی 10 آمپر است که در سوال (الف) محاسبه کردیم. این مقدار 63.2٪ یا 0.632 مقدار جریان نهایی نیز با منحنیهای گذرای نشان دادهشده در بالا مطابقت دارد.
مقدار توان در اتصال سری LR
توان لحظهای که منبع ولتاژ در اختیار مدار قرار میدهد، به صورت زیر محاسبه میشود:
توان لحظهای که توسط مقاومت به صورت گرما به هدر میرود به این صورت میباشد:
مقدار توانی که به صورت انرژی پتانسیل مغناطیسی در سلف ذخیره میشود به این صورت خواهد بود:
پس توان موجود در مدار اتصال سری LR به صورت زیر محاسبه خواهد شد:
جایی که عبارت I2R نشاندهنده توان تلفشده توسط مقاومت به صورت گرما است و عبارت دوم نشاندهنده توان جذب شده توسط سلف، به صورت انرژی مغناطیسی است.