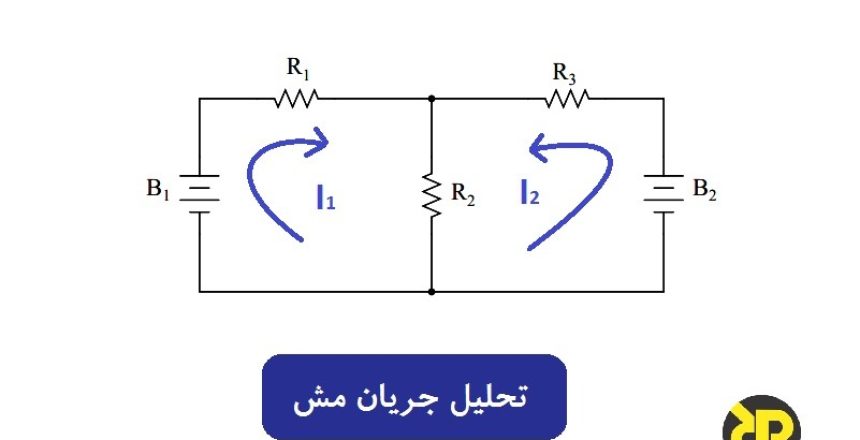
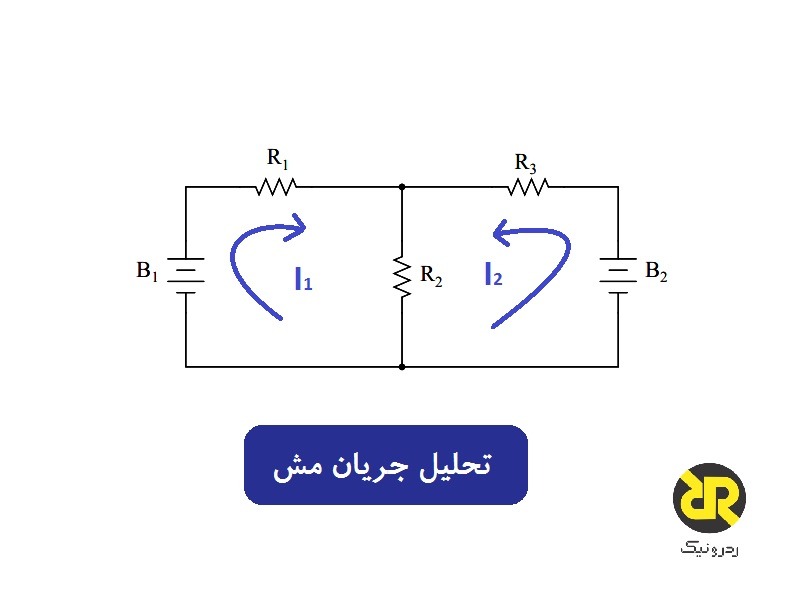
تجزیه و تحلیل جریان مش یک روش است که برای یافتن جریانهای حول یک حلقه یا مش در هر مسیر بستهای از مدار، استفاده میشود.
در حالی که قوانین کیرشهف به ما روش اصلی تجزیه و تحلیل مدارهای پیچیدهی الکتریکی را میدهد، روشهای متفاوتی برای بهبود این روش با استفاده از آنالیز جریان مش یا آنالیز ولتاژ گره وجود دارد. این روشها، منجر به کاهش محاسبات ریاضی در زمانی که با شبکههای بزرگ سروکار داریم، میشوند. این کاهش محاسبات میتواند یک مزیت بزرگ باشد.
به عنوان مثال، مدار الکتریکی زیر از آموزش قبل را در نظر بگیرید.
مدار تحلیل جریان مش
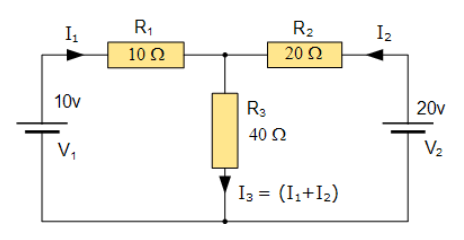
یک روش ساده برای کاهش میزان محاسبات ریاضی، تجزیه و تحلیل مدار با استفاده از معادلات جریان کیرشهف، برای تعیین جریانهای I1 و I2 در دو مقاومت است. پس نیازی به محاسبهی جریان I3 به عنوان مجموع I1 و I2 نیست. بنابراین قانون دوم ولتاژ کیرشهف بهسادگی بیان میکند:
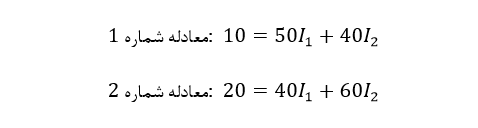
اینجا یک خط محاسبه ریاضی، ذخیره شد.
تحلیل جریان مش
یک روش سادهتر برای حل مدار بالا، استفاده از آنالیز جریان مش یا همان آنالیز حلقه بوده که گاهی اوقات روش جریانهای درحال گردش ماکسول نیز نامیده میشود. به جای برچسب زدن به جریانهای هر شاخه، ما باید هر “حلقهی بسته” را با یک جریان در حال گردش، برچسب گذاری کنیم.
بر اساس یک قاعدهی سرانگشتی، فقط در داخل حلقهها، جریانهای جاری را ساعتگرد برچسب گذاری کنید؛ زیرا هدف، حداقل یک بار پوشش دادن تمام عناصر مدار است. هر گونه جریان شاخهی مورد نیاز، ممکن است از جریان حلقه یا مش مناسب (همانند قبل که از روش کیرشهف استفاده میکردیم) پیدا شود.
برای مثال: i1 = I1 ، i2 = – I2 و I3= I1 – I2.
ما در حال حاضر، معادلهی قانون ولتاژ کیرشهف را به روش قبل برای حل آنها مینویسیم؛ اما مزیت این روش این است، که اطمینان حاصل میکند تا اطلاعات به دست آمده، حداقل مورد نیاز برای حل مدار است. زیرا این اطلاعات، کلی تر است و میتواند به راحتی در قالب ماتریس قرار گیرد.
برای مثال، مدار از قسمت قبل را در نظر بگیرید.
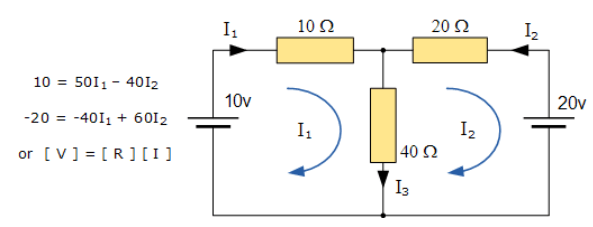
این معادلات را میتوان با استفاده از یک ماتریس امپدانس مش تنها Z به سرعت به دستآورد. هر عنصر بر روی قطر اصلی را میتوان “مثبت” درنظر گرفت که امپدانس کل هر مش است. در حالیکه، هر عنصر خارج از قطر اصلی برابر با “صفر” یا “منفی” است و نشاندهندهی عنصر مدار متصل کنندهی همهی مشهای مناسب است.
ابتدا باید درک کنیم که هنگام سروکار داشتن با ماتریسها، برای تقسیم دو ماتریس، همانند ضرب عمل نموده با این تفاوت که اولی در معکوس دومی ضرب میشود. همان طور که در شکل زیر نشان داده شدهاست.
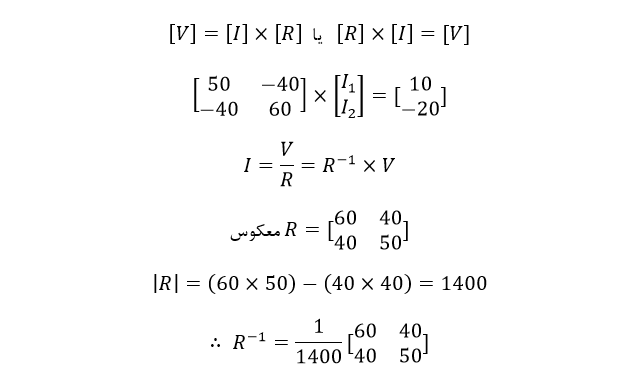
با پیدا کردن معکوس R، از آنجایی که V/R همان V*R-1 است؛ اکنون میتوانیم برای یافتن دو جریان در گردش استفاده کنیم.
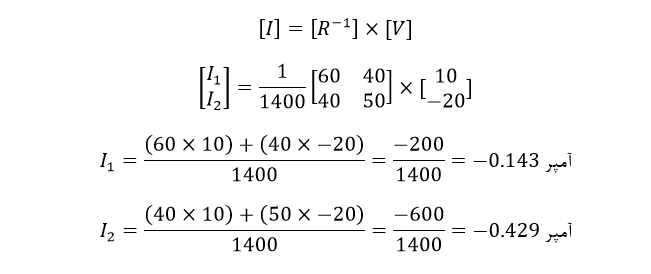
[V] : کل ولتاژ باتری برای حلقه 1 و سپس حلقه 2 را نشان میدهد.
[I] : نام جریانهای حلقه را که ما در تلاش برای یافتن آنها هستیم؛ بیان میکند.
[R] : ماتریس مقاومت است.
[R-1] : معکوس ماتریس [R] است.
درنتیجه I1 برابر با -0.143 آمپر و I2 برابر با -0.429 آمپر است.
ازآن جایی که I3 = I1 – I2 است و بنابراین جریان ترکیبی I3 بهصورت، آمپر-0.143-(-0.429) = 0.286 به دست میآید.
این مقدار جریان 0.286 آمپر، پیش از این در آموزش قانون مداری کیرشهف پیدا شدهبود.
خلاصه تحلیل جریان مش
این روش “نگاهکن-ببین” آنالیز مدار، احتمالا بهترین روش تحلیل مدار است. روش اصلی حل معادلات آنالیز جریان مش به شرح زیر است:
- به هر حلقه ورودی با جریانهای در گردش آن، برچسب بزنید (I1،I2، I3و…)
- ستون [L*1] ماتریس [V]، مجموع منابع ولتاژ هر حلقه را به ما میدهد.
- ستونهای [L*L] ماتریس [R] را برای یافتن رزیستانسهای مدار، بهصورت زیر بنویسید:

4. ماتریس یا معادله برداری [V] = [R] * [I] را درجاییکه، [I] لیست جریانهایی است که باید پیدا شوند بنویسید.
همانند استفاده از آنالیز جریان مش، می توان از آنالیز گره برای یافتن ولتاژهای دور حلقهها استفاده نمود؛ که این عمل، نیز دوباره سبب کاهش مقدار محاسبات لازم هنگام استفاده از قوانین کیرشهف خواهد شد. در آموزش بعدی مرتبط به تئوری مدار DC، نگاهی به آنالیز ولتاژ گره برای انجام این کار خواهیمداشت.