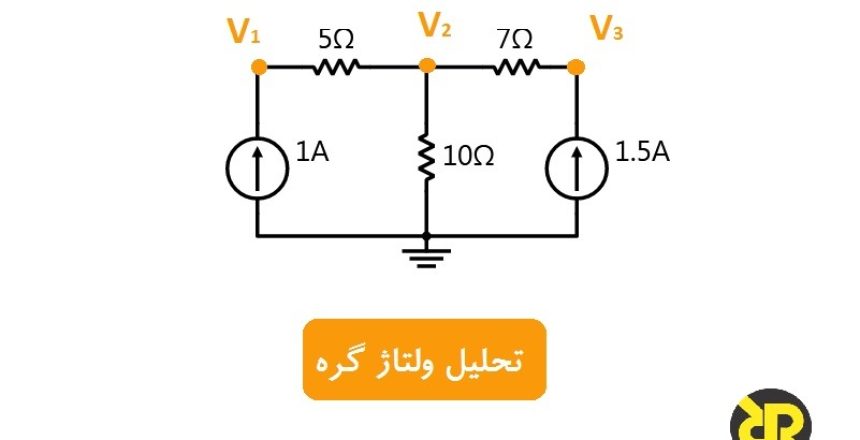
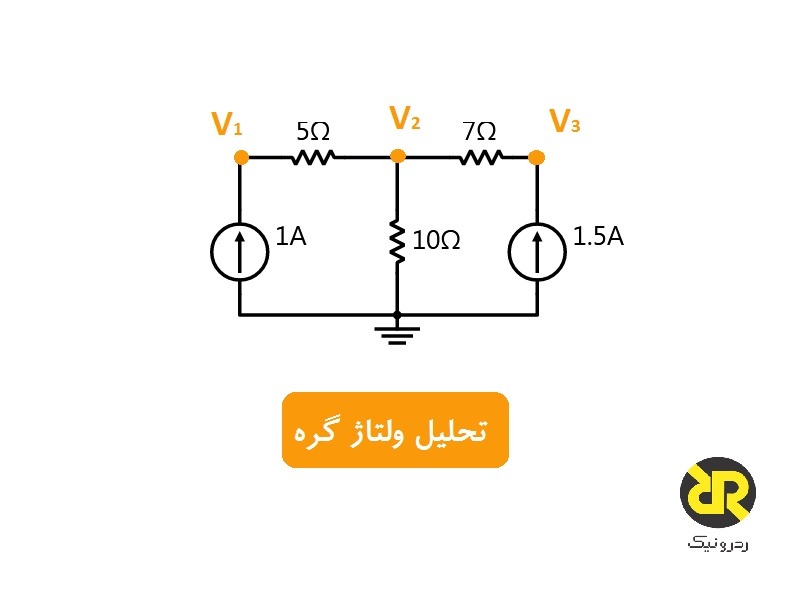
تجزیه و تحلیل ولتاژ گره، مقدار مجهول افت ولتاژ را در یک مدار، بین گرههای مختلف، نشان میدهد که یک اتصال مشترک برای دو یا تعداد بیشتری از عناصر مدار، فراهم میکند.
آنالیز ولتاژ گره، آنالیز مش قبلا گفته شده را کامل میکند؛ زیرا به همان اندازه قدرتمند است و براساس مفاهیم مشابه آنالیز ماتریس است. همانگونه که از نامش مشخص است؛ آنالیز ولتاژ گره، از معادلات “گره” برای یافتن پتانسیلهای ولتاژ در مدار استفاده میکند.
بنابراین با جمعکردن همهی ولتاژهای گره، نتیجه خالص برابر با صفر خواهدبود. پس اگر تعداد “n” گره در مدار باشد، “n-1” معادلهی گره مستقل وجود خواهد داشت که به تنهایی برای توصیف و حل مدار کافی خواهدبود.
در هر نقطهی گره، معادلهی قانون اول کیرشهف را بنویسید که بیان میکند: “جریانهای ورودی به هر گره برابر با جریانهای خروجی از آن گره است“. سپس هر جریان را بر حسب ولتاژ دو سر شاخه بیان کنید. برای “n” گره، یک گره به عنوان گره مرجع تعیین شده و سایر ولتاژها با توجه به این گره مشترک، ارجاع یا اندازهگیری میشوند.
بهعنوان مثال، مدار آموزش قبل را در نظر بگیرید:
تحلیل ولتاژ گره برای یک مدار
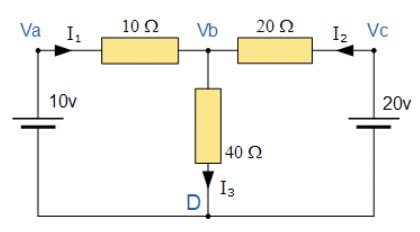
در مدار بالا، گره D بهعنوان گره مرجع انتخاب شدهاست و سه گره دیگر، دارای ولتاژ فرض شده Va ،Vb و Vc نسبت به گره مرجع D هستند. برای مثال:
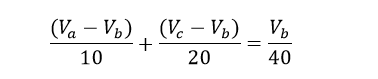
از آن جایی که، Va = 10v و Vc = 20v است؛ Vb به آسانی بدست میآید:
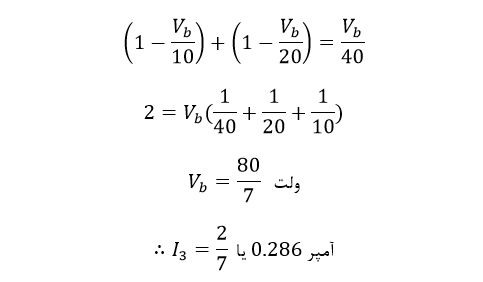
دوباره این مقدار جریان 0.286 آمپر، پیش از این در آموزش قبلی قانون مداری کیرشهف پیدا شدهبود.
از هر دو روش آنالیز مش و گره که تا کنون مورد بررسی قرار دادیم؛ این روش، سادهترین روش برای حل این مدار خاص است. به طور کلی تجزیه و تحلیل ولتاژ گره، زمانی مناسبتر است که تعداد بزرگی منبع جریان در اطراف مدار وجود داشتهباشد. پس شبکهی مربوطه تعریف خواهدشد :[I] = [Y][V]
که در اینجا
[I] منابع جریان جاری در مدار،
[V] ولتاژ گرههایی که باید یافت شوند
[Y] ادمیتانس ماتریس شبکه است که [V] را بر [I] اعمال میکند.
هستند.
خلاصه تحلیل ولتاژ گره
روش پایه برای حل معادلات آنالیز گره به شرح زیر است:
- بردارهای جریان را بنویسید. فرضکنید که جریانهای داخل یک گره، مثبت باشند؛ یعنی (N*1) ماتریس برای “N” گرهی مستقل وجود دارد.
- ماتریس ادمیتانس [Y] را بنویسید. به طوری که:

3. برای یک شبکه با “N” گرهی مستقل، [Y] برابر با یک ماتریس (N*N) بوده و Ynn مثبت و Yjk منفی یا صفر، خواهد بود.
4. بردار ولتاژ برابر با (N*L) بوده و لیستی از ولتاژهای “N” است؛ که باید پیداشوند.
تاکنون مشاهده نمودیم تعدادی قضیه وجود دارند که آنالیز مدارهای خطی را ساده میکنند. در آموزش بعدی، نگاهی به قضیه تونن خواهیم داشت؛ که به شبکهی تشکیلشده از مقاومتهای خطی و منابع اجازه میدهد تا با یک مدار معادل با یک منبع ولتاژ تنها و یک مقاومت سری، نمایش دادهشوند.