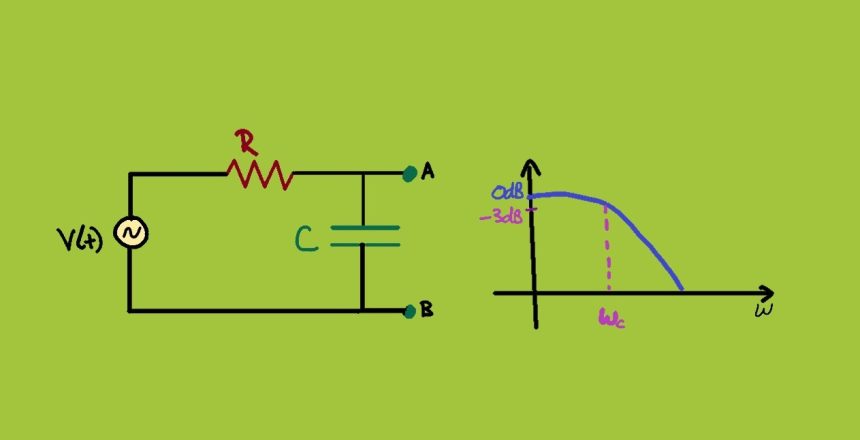
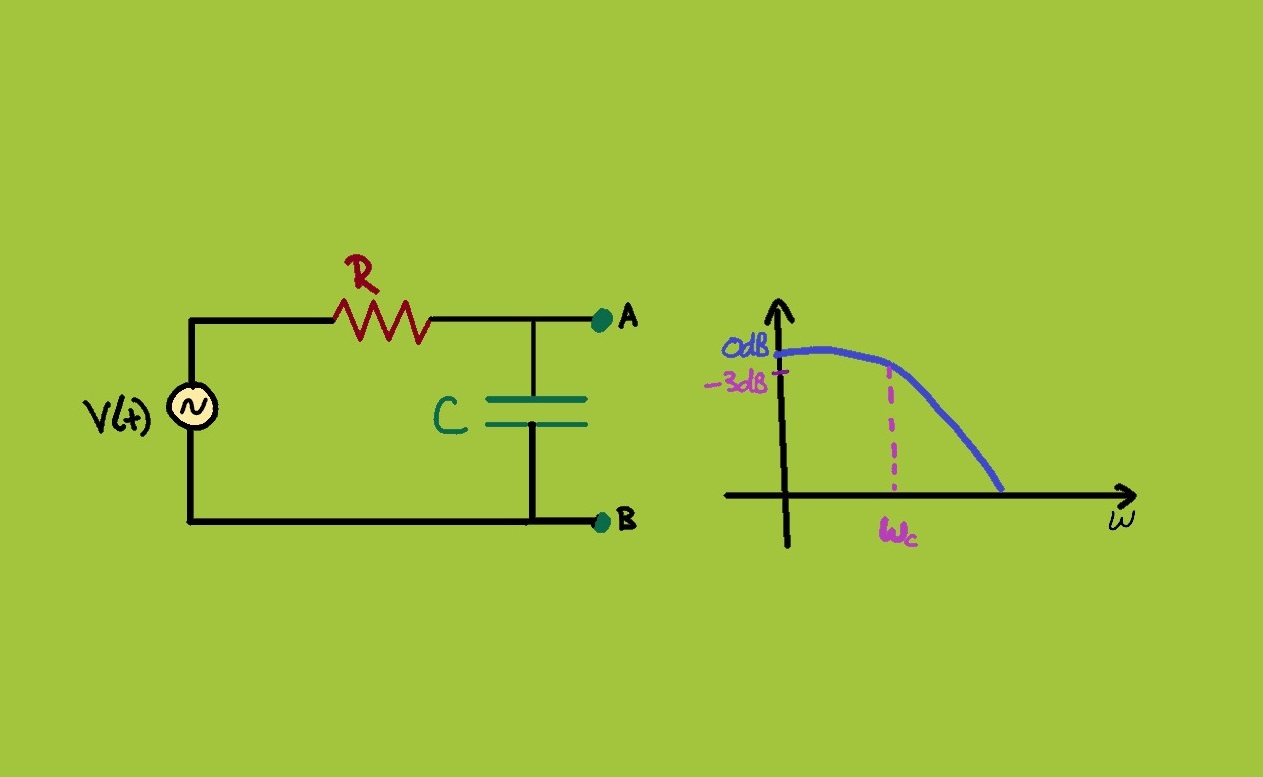
فیلتر پایین گذر مداری است که میتوان برای اصلاح، تغییر شکل یا بلاک کردن تمامی فرکانسهای بالای ناخواسته یک سیگنال الکتریکی به کار برد و تنها فرکانسهای موردنظر طراح مدار اجازه عبور دارند.
به عبارت دیگر این فیلترها سیگنالهای ناخواسته را حذف میکنند و یک فیلتر ایدهآل میتواند سیگنالهای ورودی سینوسی را بر اساس فرکانسهای تکتک سینوسیها جدا کرده و فرکانسهای مورد نظر را عبور دهد. در کاربردهای فرکانس پایین (حداکثر تا 100 کیلوهرتز) عموما فیلترهای پسیو با استفاده از یک شبکه ساده RC (مقاومتی-خازنی) ساخته میشوند، اما کاربردهای فرکانس بالا (بیش از 100 کیلو هرتز) معمولا از اجزای RLC (مقاومتی- سلفی- خازنی) ساخته میشوند.
فیلترهای پسیو از اجزای پسیو همچون مقاومتها، خازنها و سلفها ساخته میشوند و اجزای تقویتکننده (ترانزیستورها، تقویتکننده عملیاتی و غیره) ندارند پس گین سیگنال وجود ندارد و بنابراین سطح خروجی همواره از سطح ورودی پایینتر است.
فیلترها بر اساس محدوده فرکانسی سیگنالها که میتواند از شبکه آنها عبور کند نامگذاری میشوند؛ بقیه محدوده فرکانسی بلاک شده یا اصطلاحا «تضعیف» میشوند. رایجترین طراحیهای فیلترهای مورد استفاده عبارتنداز:
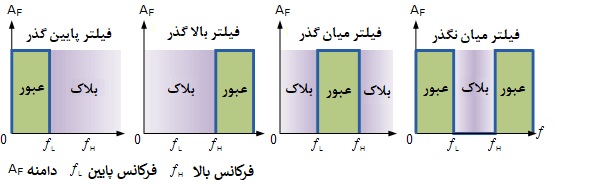
- فیلتر پایینگذر: فیلتر پایینگذر اجازه عبور فرکانسهای پایین، از فرکانس صفر تا فرکانس قطع فیلتر (fC) را میدهد و باقی محدوده فرکانسی بالا بلاک خواهد شد.
- فیلتر بالاگذر: فیلتر بالاگذر اجازه عبور فرکانسهای بالا، از فرکانس قطع فیلتر (fC) تا فرکانس بینهایت را میدهد و باقی محدوه فرکانسی پایین بلاک خواهد شد.
- فیلتر میانگذر: فیلتر میانگذر اجازه عبور باند فرکانسی خاص بین دو نقطه فرکانسی را میدهد و از عبور فرکانسهای بالا و پایین این محدوده ممانعت میکند.
فیلترهای پسیو درجه اول ساده را میتوان با اتصال یک مقاومت و یک خازن به صورت سری در دوسر یک سیگنال ورودی (Vin) ایجاد کرد و برای برداشتن خروجی (Vout) میتوان از دو سر یکی از المانهای مقاومت یا خازن استفاده کرد.
بسته به اینکه مقاومت و خازن را با توجه به سیگنال خروجی به چه ترتیبی وصل کنیم، نوع ساختار فیلتر را تعیین میکند که منجر به فیلتر پایینگذر یا فیلتر بالاگذر میشود.
از آنجایی که کار هر فیلتر این است که سیگنالهای باند فرکانسی موردنظر را بدون دستکاری از شبکه خود عبور دهد و باقی فرکانسهای ناخواسته را بلاک کرده یا تضعیف نماید، میتوانیم نمودار مشخصه دامنه یک فیلتر ایدهآل را با کمک منحنیهای پاسخ فرکانسی ایدهآل 4 فیلتر پایه شکل زیر بیان کنیم.
منحنیهای پاسخ فیلتر ایدهآل
فیلترها را میتوان به دو بخش مجزا تقسیم کرد: فیلترهای پسیو و فیلترهای اکتیو. فیلترهای اکتیو دارای ابزارهای تقویتکننده هستند تا قدرت سیگنال را افزایش دهند اما فیلترهای پسیو ابزار تقویتکننده ندارند تا سیگنال را تقویت کنند. از آنجایی که دو جز پسیو در داخل فیلترهای پسیو وجود دارد، سیگنال خروجی نسبت به سیگنال ورودی دامنه کوچکتری دارد، پس فیلترهای پسیو RC سیگنال را تضعیف میکنند و گین کمتر از یک (واحد) دارند.
فیلتر پایینگذر میتواند ترکیبی از ظرفیت خازنی، اندوکتانس یا مقاومت باشد که برای ایجاد تضعیف، بالای فرکانس مشخص و تضعیف کم یا بدون تضعیف زیر آن فرکانس طراحی شدهاست. فرکانسی که در آن قطعشدگی اتفاق میافتد را فرکانس «قطع» یا «گوشه» مینامند.
سادهترین فیلترهای پایینگذر از یک مقاومت و خازن تشکیل شدهاند، اما فیلترهای پایینگذر پیچیدهتر ترکیبی از سلفهای سری و خازنهای موازی هستند. در این مقاله به سادهترین نوع فیلتر پایینگذر RC دو جزئی پسیو می پردازیم.
فیلتر پایینگذر
یک فیلتر غیرفعال پایین گذر RC یا LPF را میتوان به راحتی با اتصال سری یک مقاومت با یک خازن مطابق شکل زیر ساخت. در این نوع آرایش فیلتر، سیگنال ورودی (VIN) به ترکیب سری اعمال میشود (هر دو مقاومت و خازن با هم) اما سیگنال خروجی (VOUT) فقط از دو سر خازن گرفته میشود.
این نوع فیلتر به طور کلی به عنوان «فیلتر درجه اول» یا «فیلتر یک قطبی» شناخته میشود، چرا مرتبه اول یا تک قطبی؟ زیرا تنها «یک»جزء راکتیو، خازن، در مدار دارد.
مدار فیلتر پایین گذر RC
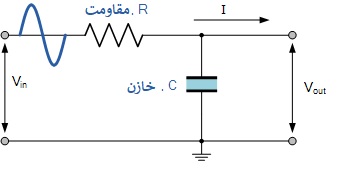
همانطور که قبلا در مقاله راکتانس خازنی ذکر شد، راکتانس خازن با فرکانس رابطه معکوس دارد، در حالی که مقدار مقاومت با تغییر فرکانس ثابت میماند. در فرکانسهای پایین، راکتانس خازنی (XC) خازن در مقایسه با مقدار مقاومت R بسیار بزرگ خواهد بود.
این بدان معناست که افت پتانسیل VC در دوسر خازن بسیار بزرگتر از افت پتانسیل VR دوسر مقاومت خواهد بود. در فرکانسهای بالا برعکس این امر اتفاق میافتد که به دلیل تغییر در مقدار راکتانس خازنی، VC کوچک و VR بزرگ است.
در حالی که مدار بالا مربوط به یک مدار فیلتر پایین گذر RC است، همچنین میتوان آن را به عنوان یک مدار تقسیم مقاومتی متغیر وابسته به فرکانس، مشابه آنچه در مقاله مقاومتها بیان کردیم در نظر گرفت. در آن آموزش از معادله زیر برای محاسبه ولتاژ خروجی برای دو مقاومت متصل به صورت سری استفاده کردیم.
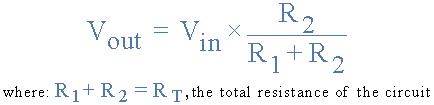
جایی که R1+R2=RT مقاومت کل مدار است.
همینطور میدانیم که راکتانس خازنی یک خازن در یک مدار متصل به وردی متناوب (AC) به این صورت به دست میآید:
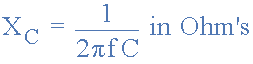
مقاومت در برابر عبور جریان در یک مدار AC را امپدانس مینامند و با Z نشان میدهند. برای یک مدار سری شامل یک مقاومت به صورت سری با یک حازن، امپدانس مدار با فرمول زیر محاسبه میشود:
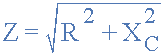
با جایگزینی این معادله امپدانس در معادله تقسیم ولتاژی خواهیم داشت:
معادله تقسیم ولتاژی RC
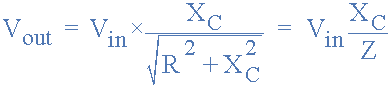
پس با استفاده از معادله تقسیم ولتاژی دو مقاومت سری و جایگزینی معادله امپدانس توانستیم ولتاژ خروجی فیلتر RC را برای هر فرکانس داده شده محاسبه کنیم.
مثال اول فیلتر پایینگذر
یک مدار پایینگذر شامل یک مقاومت 47 کیلواهم یا یک خازن 47 نانوفاراد به صورت سری بسته شده و این دو به یک منبع ولتاژ سینوسی 10 ولت متصل هستند. ولتاژ خروجی را در فرکانسهای 100 هرتز و 10 کیلوهرتز بیابید.
ولتاژ خروجی در فرکانس 100 هرتز
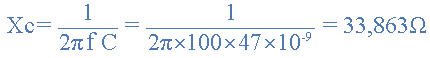
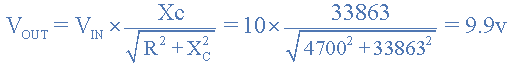
ولتاژ خروجی در فرکانس 10 کیلوهرتز یا 10000 هرتز
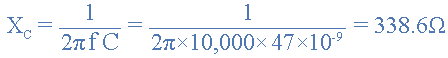
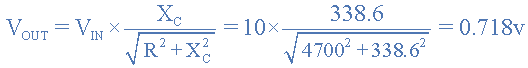
پاسخ فرکانسی
از نتیجه مثال بالا درمییابیم که با افزایش فرکانسی اعمالی بر شبکه RC از 100 هرتز تا 10 کیلوهرتز، بیشتر افت ولتاژ بر روی دوسر خازن افتاده و بنابراین ولتاژ خروجی (VOUT) مدار از 9/9 ولت تا 718/0 ولت کاهش یافته است.
با رسم نمودار ولتاژ خروجی شبکه بر اساس تغییرات فرکانس، منحنی پاسخ فرکانسی یا نمودار بد مدار فیلتر پایینگذر به صورت شکل زیر به دست میآید.
پاسخ فرکانسی فیلتر پایینگذر درجه اول
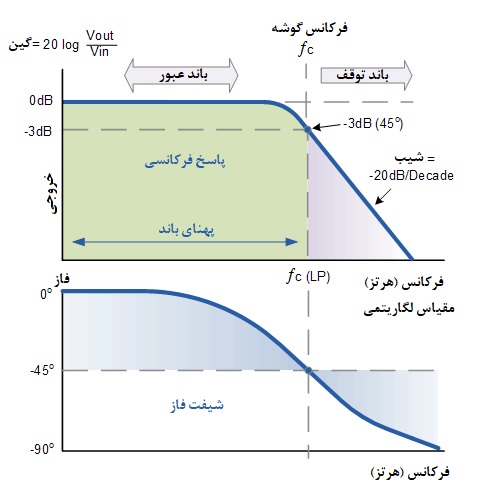
نمودار بد پاسخ فرکانس فیلتر را برای فرکانسهای پایین تقریبا مسطح نشان میدهد و تمام سیگنال ورودی مستقیما به خروجی ارسال میشود و در نتیجه یک بهره نزدیک به 1 به نام واحد ایجاد میشود تا زمانی که به نقطه فرکانس قطع خود (fC) برسد. این به این دلیل است که راکتانس خازن در فرکانسهای پایین زیاد است و اجازه عبور جریان از خازن را نمیدهد.
پس از نقطه فرکانس قطع، پاسخ مدار با شیب 20- دسیبل در هر دهه یا 6- دسیبل در هر اکتاو ادامه مییابد تا به صفر برسد که اصطلاحا این شیب را roll-off مینامند. توجه داشته باشید که این زاویه شیب، همیشه برای هر ترکیب RC یکسان خواهد بود.
هر سیگنال فرکانس بالا اعمالی بر مدار فیلتر پایینگذر بالای نقطه فرکانس قطع به شدت تضعیف میشود، یعنی به سرعت کاهش مییابد. این امر به این دلیل اتفاق میافتد که در فرکانسهای بسیار بالا راکتانس خازن به قدری کم میشود که باعث ایجاد شرایط اتصال کوتاه روی پایانههای خروجی شده و در نتیجه خروجی صفر میشود.
سپس با انتخاب دقیق ترکیب مقاومت و خازن، میتوانیم یک مدار RC ایجاد کنیم که به طیفی از فرکانسهای زیر یک مقدار معین اجازه میدهد بدون تاثیر از مدار عبور کنند، در حالی که فرکانسهای اعمال شده به مدار بالای این نقطه قطع تضعیف میشوند. چنین مداری معمولا فیلتر پایینگذر نامیده میشود.
برای این نوع «فیلتر پایینگذر»، تمام فرکانسهای زیر نقطه قطع (fC) که بدون تضعیف یا بدون تغییر هستند، در باند عبور فیلتر هستند. این ناحیه باند عبور نیز نشاندهنده پهنای باند فیلتر است. هر فرکانس سیگنال بالاتر از این نقطه قطع، معمولا در باند توقف فیلتر قرار دارد و تا حد زیادی تضعیف میشود.
این فرکانس قطع، گوشه یا نقطه شکست به عنوان نقطه فرکانسی تعریف میشود که در آن راکتانس خازنی و مقاومت برابر هستند( R = Xc = 47kΩ ). هنگامی که این اتفاق می افتد، سیگنال خروجی به 7/70 % از مقدار سیگنال ورودی رسیده یا 3- دسیبل کاهش مییابد. بنابراین، در R = Xc ، خروجی نیمی از سیگنال ورودی نیست. این امر به این دلیل اتفاق میافتد که این مقدار برابر است با مجموع برداری این دو و بنابراین 707/0ورودی است.
از آنجایی که فیلتر حاوی یک خازن است، زاویه فاز (Φ) سیگنال خروجی از سیگنال ورودی عقب افتاده و در فرکانس قطع 3- دسیبل با تاخیر فاز 45- درجه روبرو میشود. این امر به دلیل زمان صرف شده برای شارژ صفحات خازن، با تغییر ولتاژ ورودی است که در نتیجه ولتاژ خروجی (ولتاژ دو طرف خازن) از سیگنال ورودی عقب می ماند. هر چه فرکانس ورودی اعمال شده به فیلتر بیشتر باشد، تاخیر خازن بیشتر می شود و مدار بیشتر و بیشتر از ورودی عقب میافتد (اصطلاحا میگویند که خروجی Lag دارد).
نقطه فرکانس قطع و زاویه شیفت فاز را با استفاده از معادلات آتی میتوان یافت:
شیفت فاز و فرکانس قطع
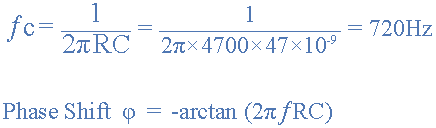
پس برای مثال ساده ما در مورد مدار فیلتر پایینگذر، فرکانس قطع برابر با 720 هرتز است که در این فرکانس، ولتاژ خروجی 7/70 % ولتاژ ورودی است و شیفت فازی برابر با 45- درجه میباشد.
فیلتر پایینگذر درجه دوم
تا اینجا دیدیم که فیلترهای RC مرتبه اول ساده را میتوان با اتصال یک مقاومت به صورت سری با یک خازن ایجاد کرد. این آرایش تک قطبی یک شیب 20- دسیبل در هر دهه ایجاد میکند که موجب تضعیف فرکانسهای بالاتر از نقطه قطع در فرکانس 3- دسیبل میشود. با این حال، گاهی اوقات در مدارهای فیلتر، این زاویه شیب 20- دسی بل بر هردهه (6- دسی بل بر هر اکتاو) ممکن است برای حذف سیگنال ناخواسته کافی نباشد، پس میتوان از دو طبقه فیلتر مطابق شکل استفاده کرد.
فیلتر پایینگذر درجه دوم
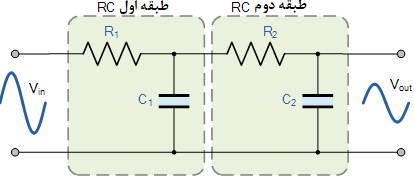
مدار فوق از دو فیلتر پایینگذر مرتبه اول پسیو متصل به یکدیگر یا «کسکود» برای تشکیل یک شبکه فیلتر مرتبه دوم یا دو قطبی استفاده میکند. بنابراین میتوانیم ببینیم که یک فیلتر پایینگذر مرتبه اول را میتوان با اضافه کردن یک شبکه RC اضافی به آن به یک نوع مرتبه دوم تبدیل کرد و هرچه طبقات RC بیشتری اضافه کنیم، مرتبه فیلتر بالاتر میرود.
اگر تعداد (n) طبقه RCبا هم کسکود شوند، مدار فیلتر RC حاصل به عنوان یک فیلتر مرتبه n با شیب 20 – در دهر دهه شناخته می شود.
به عنوان مثال، یک فیلتر مرتبه دوم دارای شیب 40- بر هر دهه (12- در هر اکتاو) است، یک فیلتر مرتبه چهارم دارای شیب 80- بر هر دهه (24- در هر اکتاو) است. این امر بدان معنی است که با افزایش طبقات فیلتر، شیب roll-off تندتر میشود و پاسخ باند توقف واقعی فیلتر، به ویژگیهای باند توقف ایدهآل خود نزدیک میشود.
فیلترهای مرتبه دوم مهم هستند و به طور گسترده در طراحی فیلترها مورد استفاده قرار میگیرند زیرا وقتی با فیلترهای مرتبه اول ترکیب میشوند، میتوان فیلترهای درجه n بالاتر را با استفاده از آنها طراحی کرد. به عنوان مثال، یک فیلتر پایینگذر مرتبه سوم از اتصال سری یا کسکود یک فیلتر پایینگذر مرتبه اول و دوم تشکیل میشود.
اما کنار هم قرار دادن طبقات فیلتر RC به صورت کسکود یک جنبه منفی نیز دارد. اگرچه هیچ محدودیتی برای طبقات فیلتر وجود ندارد، اما با افزایش طبقات، گین و دقت فیلتر نهایی کاهش مییابد. هنگامی که طبقات فیلتر RC یکسان، با هم کسکود میشوند، گین خروجی در فرکانس قطع مورد نیاز (fC) به میزانی وابسته به تعداد طبقات فیلتر استفاده شده با افزایش شیب roll-off کاهش مییابد (تضعیف میشود). با استفاده از فرمول زیر می توانیم میزان تضعیف را در فرکانس قطع انتخابی به دست آوریم.
گین فیلتر پسیو پایینگذر در fC
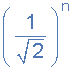
جایی که n تعداد طبقات فیلتر میباشد.
پس برای فیلتر درجه دوم، سوم و چهارم، گین به ترتیب برابر با 5/0 (6- دسیبل)، 353/0، (9- دسیبل) و 25/0 (12- دسیبل) خواهد بود. فرکانس گوشه (fC) برای فیلتر پایینگذر پسیو درجه دوم، توسط ترکیب مقاومت و خازن مشخص شده و به صورت زیر محاسبه میشود:
فرکانس گوشه فیلتر درجه دوم

در عمل با افزایش طبقات فیلتر و در نتیجه شیب roll-off آن، نقطه فرکانس گوشه 3- دسیبل فیلتر پایینگذر و همینطور فرکانس باند عبور آن، از مقدار محاسبه شده اولیه خود در بالا با مقدار تعیین شده توسط معادله زیر تغییر میکند.
فرکانس 3- دسیبل فیلتر پایینگذر درجه دوم
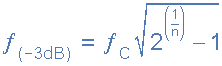
جایی که fC فرکانس قطع محاسبه شده، n درجه فیلتر و f-3dB فرکانس باند عبور جدید به دلیل افزایش درجه فیلتر میباشند.
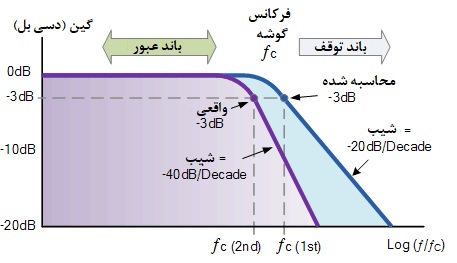
پس پاسخ فرکانسی (نمودار بد) برای یک فیلتر پایینگذر درجه دوم با فرض نقطه قطع 3- دسیبل یکسان با شکل زیر نشان داده میشود:
پاسخ فرکانسی یک فیلتر پایینگذر درجه دوم
در عمل، اجرای دقیق فیلترهای پسیو کسکود برای تولید فیلترهای مرتبه بزرگتر دشوار است زیرا امپدانس دینامیکی هر طبقه فیلتر بر شبکه مجاور آن تأثیر میگذارد. با این حال، برای کاهش اثر بارگذاری، میتوانیم امپدانس هر مرحله بعدی را 10 برابر مرحله قبلی کنیم، بنابراین R2 = 10 x R1 و C2 = 1/10 C1
شبکههای فیلتر مرتبه دوم و بالاتر عموما در مدارهای فیدبک آپآمپها استفاده میشوند و آنچه را که معمولا به عنوان فیلترهای فعال یا شبکه شیفت فاز در مدارهای نوسانگر RC شناخته میشوند، میسازند.
خلاصه فیلتر پایینگذر
بنابراین به طور خلاصه، فیلتر پایینگذر دارای یک ولتاژ خروجی ثابت از صفر هرتز (DC ) تا یک فرکانس قطع مشخص (ƒC) است. این نقطه فرکانس قطع، 707/0 برابر بهره ولتاژ مجاز یا 3 دسیبل پایینتر از دامنه فرکانس DC است.
محدوده فرکانسی «زیر» نقطه قطع fC به طور کلی به عنوان باند عبور شناخته میشود زیرا سیگنال ورودی اجازه عبور از فیلتر را دارد. محدوده فرکانسی «بالای» نقطه قطع عموما به عنوان باند توقف شناخته میشود زیرا سیگنال ورودی مسدود شده یا از عبور آن جلوگیری میشود.
یک فیلتر پایینگذر ساده مرتبه اول را میتوان با استفاده از یک مقاومت به صورت سری با یک خازن غیر قطبی (یا هر جزء راکتیو دیگر) متصل به دو سر یک سیگنال ورودی Vin ایجاد کرد، در حالی که سیگنال خروجی Vout از دوسر خازن گرفته میشود. فرکانس قطع یا نقطه 3- دسی بل را میتوان با استفاده از این فرمول استاندارد پیدا کرد. زاویه فاز سیگنال خروجی در fC برابر 45- درجه برای فیلتر پایینگذر است. به طور کلی، بهره فیلتر یا هر فیلتری برای این امر بر حسب دسی بل بیان میشود و تابعی از مقدار خروجی تقسیم بر مقدار ورودی مربوطه آن است و به صورت زیر به دست میآید:
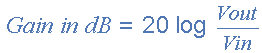
کاربردهای فیلترهای پایینگذر پسیو در تقویتکنندههای صوتی و سیستمهای بلندگو برای هدایت سیگنالهای باس فرکانس پایین به بلندگوهای باس بزرگتر، کاهش هرگونه نویز فرکانس بالا و یا اعوجاج نوع «هیس» است. فیلتر پایینگذر هنگامی که به این صورت در کاربردهای صوتی استفاده میشود، گاهی اوقات فیلتر high-cut یا treble cut نامیده میشود. اگر بخواهیم موقعیت مقاومت و خازن را در مدار عوض کنیم به طوری که ولتاژ خروجی از دوسر مقاومت گرفته شود، مداری خواهیم داشت که منحنی پاسخ فرکانس خروجی مشابه فیلتر بالاگذر را تولید میکند و در آموزش بعدی به این موضوع پرداخته شده است.
ثابت زمانی
تا به حال ما زمانی که فیلتر پایینگذر در معرض شکل موج سینوسی قرار میگیرد، به پاسخ فرکانسی آن علاقهمند بوده ایم. همچنین دیدیم که فرکانس قطع فیلترها (ƒC) محصولی از مقادیر مقاومت (R) و ظرفیت (C) در مدار نسبت به نقطه فرکانس مشخص است و با تغییر هر یک از دو جز، این نقطه فرکانس قطع افزایش یا کاهش مییابد.
همچنین میدانیم که به دلیل زمان مورد نیاز برای شارژ و سپس تخلیه خازن با تغییر موج سینوسی، سیگنال خروجی به دلیل شیفت فازی از سیگنال ورودی عقب است. این ترکیب از R و C یک اثر شارژ و دشارژ بر روی خازن ایجاد میکند که به عنوان ثابت زمانی مدار ( τ ) شناخته میشود، همانطور که در آموزش های مدار RC مشاهده کردهاید که پاسخ فیلتر در حوزه زمان را مشخص میکند.
تاو یا ثابت زمانی (τ) به گونهای با فرکانس قطع رابطه دارد:
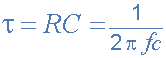
اگر بخواهیم فرکانس قطع fC را بر حسب ثابت زمانی (τ) بنویسیم:
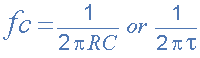
ولتاژ خروجی VOUT به ثابت زمانی و فرکانس سیگنال ورودی بستگی دارد. با یک سیگنال سینوسی که به آرامی در طول زمان تغییر میکند، همانطور که در بالا دیدیم، مدار مانند یک فیلتر پایینگذر ساده درجه 1 عمل میکند. اما اگر بخواهیم سیگنال ورودی را به سیگنالی از نوع «روشن/خاموش» به شکل «موج مربعی» که ورودی پلهای تقریبا عمودی دارد تغییر دهیم، اکنون چه اتفاقی برای مدار فیلتر میافتد. پاسخ خروجی مدار به طور چشمگیری تغییر میکند و نوع دیگری از مدار را تولید میکند که معمولا به عنوان انتگرالگیر شناخته میشود.
انتگرالگیر RC
انتگرالگیر اساسا یک مدار فیلتر پایینگذر است که در حوزه زمان کار میکند و همینطور که خازن شارژ و دشارژ میشود، سیگنال ورودی پاسخ «پله» موج مربعی را به یک خروجی به شکل موج مثلثی تبدیل میکند. شکل موج مثلثی از خطوط شیبدار متناوب مساوی، مثبت و منفی تشکیل شدهاست. همانطور که در زیر مشاهده میشود، اگر ثابت زمانی RC در مقایسه با دوره زمانی شکل موج ورودی طولانی باشد، شکل موج خروجی مثلثی شکل خواهد بود و هر چه فرکانس ورودی بالاتر باشد دامنه خروجی در مقایسه با ورودی کمتر خواهد بود.
مدار انتگرالگیر RC
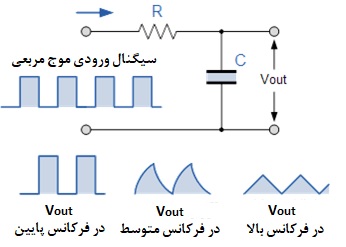
پس در مدارهای موجتولیدکن یا تغییرشکلدهنده موج، این نوع از مدار برای تبدیل کردن سیگنالهای الکترونیکی به شکلهای مختلف برای اهداف گوناگون ایدهآل است.