تفریق کننده باینری، نوع دیگری از مدارهای ترکیبی محاسباتی است ؛ که خروجی ناشی از تفریق دو عدد باینری را ، تولید میکند.
همانطور که از نامش پیدا ست ؛ یک تفریق گر باینری ، یک مدار تصمیم گیری است ؛ که دو عدد باینری را از یک دیگر ، کم میکند. برای مثال ، X-Y برای یافتن تفاوت حاصل بین دو عدد ، استفاده میشود.
برخلاف جمع کننده باینری ، که یک بیت جمع (SUM) و یک بیت نقلی (CARRY) هنگام جمع شدن دو عدد با یکدیگر ، تولید میکند ؛ یک تفریق گر باینری ، یک اختلاف (DIFFERENCE) یا D ، با استفاده از یک بیت قرضی (BORROW bit) ، B گرفته شده از ستون قبلی ، تولید میکند. پس بدیهی است ؛ که عمل تفریق ، برعکس عمل جمع است.
از درس های ریاضی در مدرسه، آموختیم ؛ که علامت منفی “-” برای محاسبهی تفریق ، استفاده میشود و هنگامی که ، یک عدد از دیگری کم میشود ؛ عدد قرضی ، درصورتی که عدد مفروق ، از عددی که از آن کم میشود ؛ بزرگ تر باشد ، نیاز است. تفریق سادهی دو عدد ده دهی (مبنای 10) زیر را ، در نظر بگیرید:

ما نمیتوانیم مستقیما عدد 8 را از 3 ، در ستون اول ، کم کنیم ؛ زیرا عدد 8 از 3 بزرگتر است. پس باید یک 10 ، عدد پایه را از ستون بعدی ، قرض کنیم و به عددی که میخواهیم از آن کم کنیم ؛ اضافه نماییم ؛ درنتیجه باید 8 را 13 کم کنیم . این 10 “قرض گرفته شده”، پس از یافتن تفاوت ، به مفروق ستون بعدی ، باز میگردد. ریاضیات سادهی مدرسه ، بیان میکند ؛ که یک 10 درصورت لزوم ، قرض بگیرید ، تفاوت را پیدا کنید و سپس عدد قرضی را بازگردانید.
تفریق دو عدد باینری از یکدیگر نیز ، دارای همان ایدهی تفریق دو عدد ده دهی است. اما از آنجایی که سیستم اعداد باینری ، یک سیستم شماره گذاری در مبنای 2 است ؛ که از “0” و “1” بهعنوان دو رقم مستقل خود ، استفاده میکند؛ بنابراین ، اعداد باینری بزرگ ، که باید از یکدیگر ، تفریق شوند ؛ برحسب “0” و “1”، نمایش داده میشود.
تفریق باینری
تفریق باینری ، میتواند اشکال مختلفی ، داشته باشد ؛ اما قوانین تفریق ، در هر روشی که استفاده میشود ؛ یکسان است. از آنجایی که ، نماد باینری دارای دو رقم است ؛ تفریق “0” از “0” یا “1” ، یک نتیجهی بدون تغییر دارد. یعنی 0-0=0 و 1-0=0 خواهد بود. تفریق “1” از “1” برابر با “0” خواهد بود ؛ اما تفریق “1” از “0”، نیاز به یک رقم قرضی دارد. به بیان دیگر ، 0-1 باید یک رقم قرضی ، داشتهباشد.
تفریق باینری دو بیت

برای مثال سادهی تفریق 1 بیتی بالا ، اگر بیت قرضی نادیده گرفته شود ؛ نتیجهی تفریق باینری آنها شبیه به یک گیت Ex-OR است. برای جلوگیری از هرگونه سردرگمی در این آموزش ، زیرا هم ورودی باینری تفریق گر برچسب B خورده است و هم خروجی بیت قرضی نتیجه از تفریق گر باینری ، دارای برچسب B است ؛ دو بیت ورودی را با برچسب X برای عددی که از آن کم میکنیم و Y برای عدد مفروق ، برچسب گذاری میکنیم . سپس جدول درستی نتیجه ، تفاوت بین دو بیت ورودی تفریق گر باینری واحد را ، بهصورت زیر ، به ما خواهد داد:
گیت دو ورودی Ex-OR
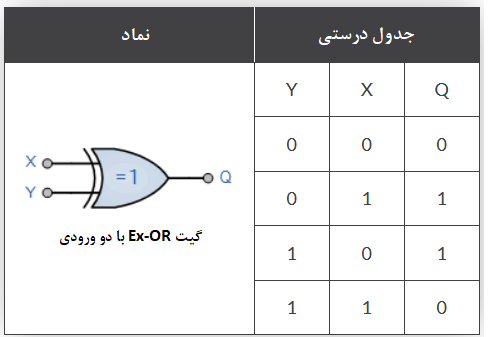
همانند جمع کنندهی باینری ، اختلاف بین دو رقم ، تنها زمانی “1” خواهد بود ؛ که دو ورودی طبق آنچه توسط عبارت Ex-OR بیان میشود ؛ برابر نباشند. بنابراین ، نیاز به یک خروجی اضافه ، برای تولید بیت قرضی ، زمانیکه ورودی X=0 و ورودی Y=1 است ؛ میباشد. متاسفانه ، هیچ گیت منطقی استانداردی ، برای تولید خروجی برای این ترکیب بندی خاص ورودی های X و Y، وجود ندارد.
اما ، ما میدانیم ؛ که یک گیت AND ، زمانیکه دو ورودی X و Y آن ، برابر با “1”(HIGH) باشد؛ خروجی “1” تولید میکند. پس اگر ما یک معکوس کننده یا گیت NOT بهعنوان مکمل ورودی X قبل از اتصال به گیت AND قرار دهیم ؛ میتوانیم خروجی قرضی موردنیاز را ، برای زمانیکه X=0 و Y=1 است ، تولید نماییم.

پس ، ترکیب کردن گیت Ex_OR با یک ترکیب گیت NOT-AND ، به ما یک مدار تفریق گر باینری دیجیتال ساده ، خواهد داد ؛ که معمولا با نام نیم تفریق گر ، شناخته میشود و در زیر ، نشان داده شده است.
یک مدار نیم تفریق گر
یک نیم تفریق گر ، یک مدار منطقی است ؛ که عمل تفریق را بر روی دو رقم باینری ، انجام میدهد. این نیم تفریق گر، یک اختلاف و یک بیت قرضی ، برای مرحلهی بعد ، تولید میکند.
نیم تفریق گر با خروجی قرضی
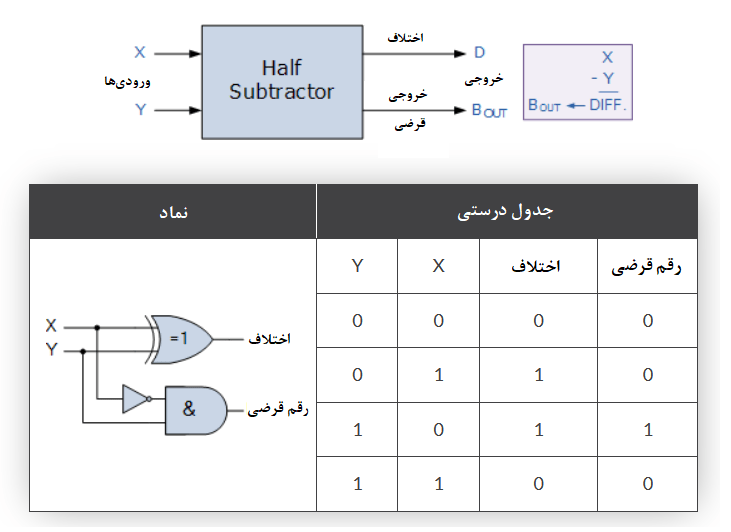
از جدول درستی بالا برای نیم تفریق کننده ، میتوانیم ببینیم که خروجی اختلاف (DIFFERENCE) ،D نتیجهی گیت انحصاری OR و خروجی قرضی (Borrow-out) ، Bout نتیجهی ترکیب NOT-AND است. پس عبارت بولین برای یک نیم تفریق گر، بهصورت زیر است:
برای بیت اختلاف:
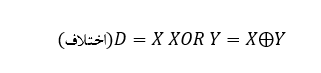
برای بیت قرضی:
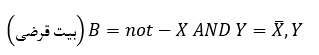
اگر ما دو عبارت بولین از نیم تفریق گر را با نیم جمع کننده، مقایسه کنیم؛ میبینیم که دو عبارت برای جمع (جمعکننده) و اختلاف (تفریقگر) دقیقا برابر بوده و بهدلیل نوع عملکرد گیت Ex_OR باید همین گونه باشد. عبارات بولین برای رقم قرضی تفریق گر باینری، بسیار مشابه به رقم نقلی برای جمع کننده است. پس تنها چیزی که برای تبدیل یک نیم جمع کننده به نیم تفریق گر نیاز است؛ معکوس کردن ورودی X که عددی بعدی، از آن کم میشود؛ میباشد.
یکی از معایب اصلی مدار نیم تفریق گر، زمانیکه بهعنوان تفریق گر باینری بهکار میرود؛ این است؛ که هنگام تفریق چند بیت داده از یکدیگر، هیچ پیش بینی برای “رقم قرضی ورودی(Borrow-in)” از مدار قبلی، وجود ندارد. بنابراین، نیاز به تولید یک مدار تفریق کننده کامل، برای درنظر گرفتن ورودی borrow-in از مدار قبلی، میباشد.
یک مدار تفریقگر کامل
تفاوت اصلی بین مدار تفریق گر کامل و نیم تفریق گر پیشین، این است؛ که تفریق گر کامل، دارای سه ورودی میباشد. دو ورودی دادهی تک بیتی X (عددی که از آن تفریق، انجام میشود) و Y(مفروق)، همانند قبل ، بهعلاوهی یک ورودی قرضی(B-in) اضافی که بتواند رقم قرضی را از فرآیند تفریق مرحلهی قبلی، دریافت کند؛ که در زیر نشان داده شده است.
بلوک دیاگرام تفریقگر کامل
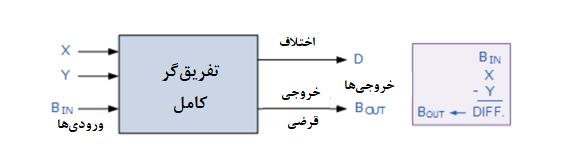
پس مدار ترکیبی یک “تفریق گر کامل”، عملیات تفریق را بر روی سه بیت باینری، برای تولید خروجی های اختلاف،D و خروجی نقلی B، انجام میدهد. دقیقا همانند مدار جمع کننده ی باینری، میتوان یک تفریق گر کامل را، دو نیم تفریق گر که به یک دیگر اتصال یافتهاند؛ فرض نمود؛ درحالیکه، نیم تفریق گر اول، رقم قرضی خود را به نیم تفریق گر دوم، انتقال میدهد.
بلوک دیاگرام تفریقگر کامل
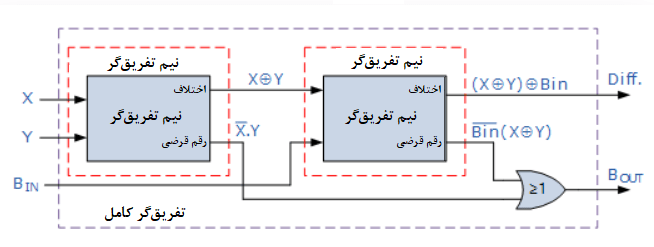
از آنجایی که، مدار تفریق گر کامل در بالا، اساسا دو نیم تفریق گر اتصال یافته به یک دیگر، را نشان میدهد؛ جدول درستی برای تفریقگر کامل، دارای هشت ترکیب ورودی مختلف، بهدلیل وجود سه متغیر ورودی است. یعنی شامل بیت های داده و ورودی قرضی (Borrow-in(BIN)) به همراه بیت خروجی اختلاف (D) و بیت خروجی قرضی (Borrow-out(Bout)) میباشد
جدول درستی تفریقگر کامل
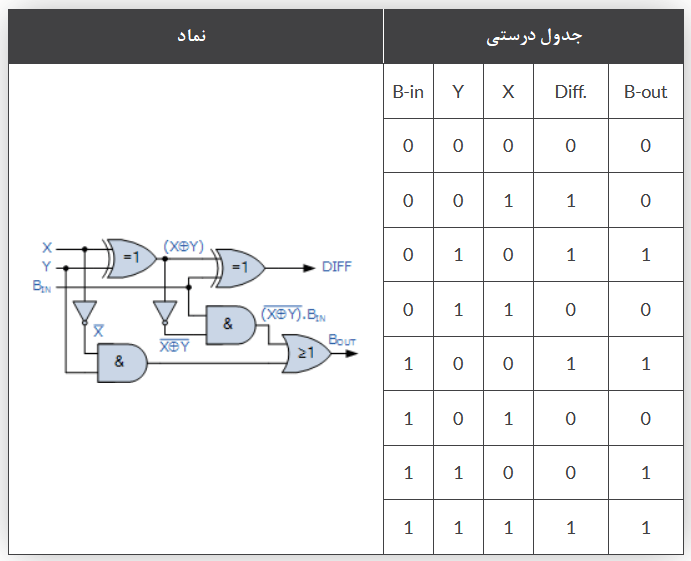
بنابراین، عبارت بولین برای تفریقگرکامل بهصورت زیر است:
برای بیت اختلاف (D):
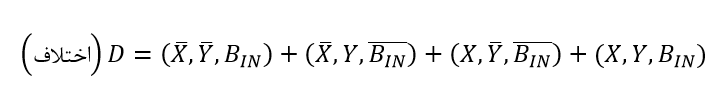
که میتواند بهصورت زیر ساده شود:
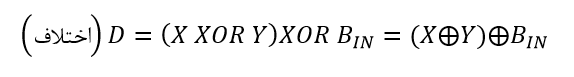
برای بیت خروجی قرضی(Bout):
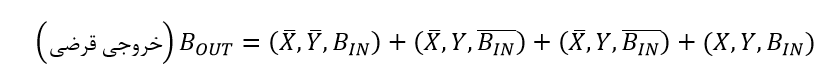
که میتواند بهصورت زیر ساده شود:
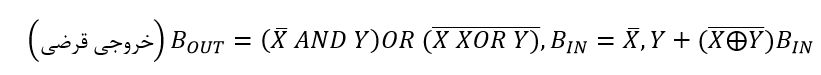
یک تفریق گر باینری n بیت
همانند جمعکننده ی باینری ، میتوان n عدد تفریق گر کامل تک بیتی را به یکدیگر متصل یا “کسکید” نمود؛ تا بتوان دو عدد موازی n بیتی را از هم کم کرد. برای مثال، دو عدد باینری 4 بیتی. پیش از این گفتیم؛ که تنها تفاوت بین جمعکننده ی کامل و تفریق گر کامل، معکوس شدن یکی از ورودیهاست.
بنابراین، با استفاده از یک جمعکنندهی n بیتی و n عدد معکوسکننده (گیت NOT)، میتوان فرآیند تفریق را به جمع تبدیل نمود. زیرا میتوان از نماد مکمل دو در تمام بیت های مفروق و تنظیم ورودی نقلی بیت با کمترین ارزش به منطق “1”(HIGH) استفاده نمود.
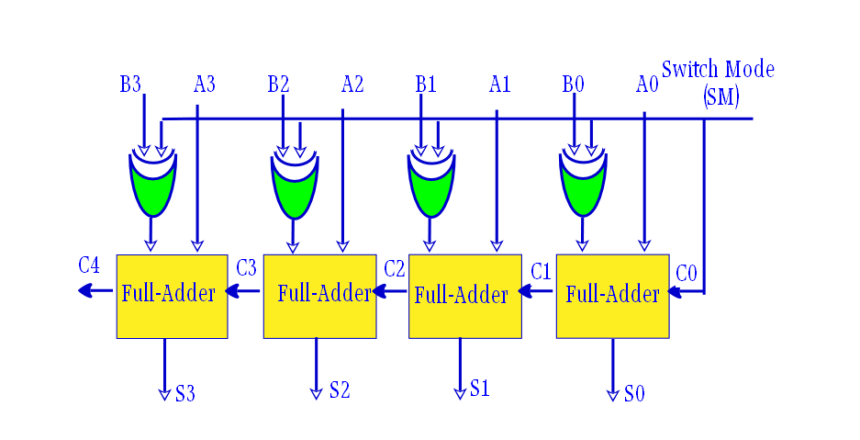
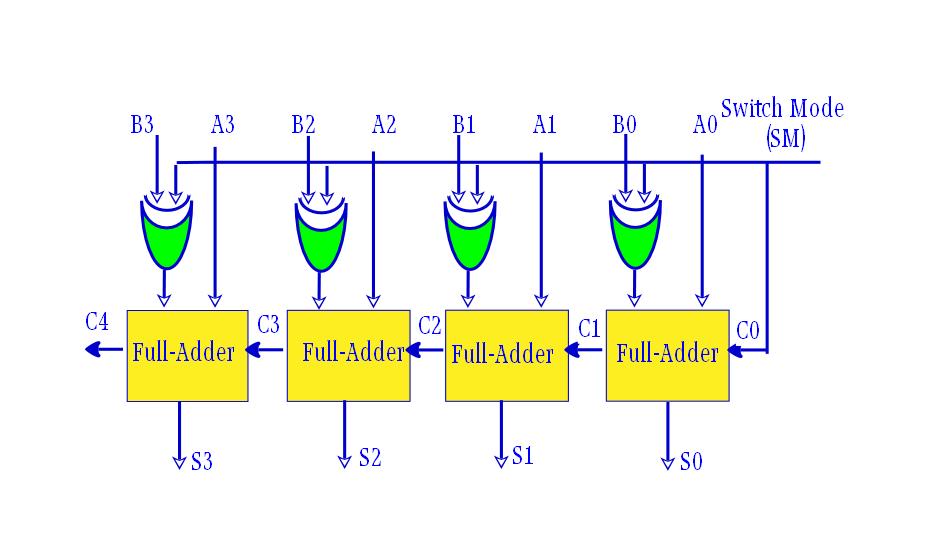
تفریق گر باینری با استفاده از مکمل دو
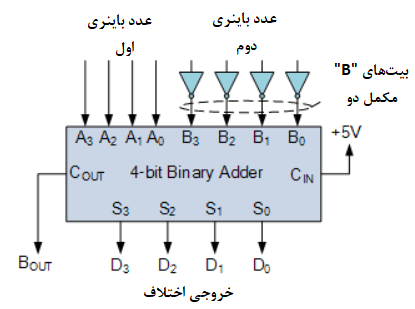
پس میتوان از IC های جمع کنندهی کامل 4 بیتی، مانند 74LS283 و CD4008 برای عمل تفریق، به سادگی و با استفاده از مکمل دو نمودن مفروق، B استفاده نمود. زیرا X-Y برابر با X+(-Y) است؛ که بهمعنای X بهعلاوهی مکمل دو Y است.
اگر بخواهیم از جمع کننده ی 4 بیتی، یک بار دیگر برای جمع استفاده کنیم؛ تنها نیاز است که ورودی نقلی (CIN) را در حالت LOW و یعنی منطق “0” قرار دهیم. زیرا ما میتوانیم IC جمعکنندهی 4 بیتی، مانند 74LS83 یا 74LS283 را بهعنوان یک جمع کنندهی کامل یا یک تفریق گر کامل استفاده کنیم. چون، آنها بهعنوان یک مدار جمع کننده/تفریق گر واحد، با ورودی کنترلی واحد، برای انتخاب بین دو عملکرد، در دسترس میباشند.