کد BCD روشی برای تبدیل اعداد دسیمال به معادل باینری آن است. همانطور که در مقالات پیشین اشاره شد، در مدارهای دیجیتالی و الکترونیکی از کدهای باینری بسیار متفاوتی استفاده میشود که هرکدام کاربرد خاص خود را دارند.
محاسبات روزانه در جهان بر مبنای ده (اعداد اعشاری) ارائه میشوند، از طرفی سیستمهای الکترونیکی و دیجیتال تنها قادر به درک اعداد باینری هستند، از این رو تبدیل اعداد دسیمال به اعداد باینری دارای اهمیت فراوان است، که یکی از این روشها استفاده از کد BCD است.
با توجه به آموزشهای قبلی، یک کد باینری n بیتی، شامل گروهی از n بیت خواهد بود که میتواند حداکثر ترکیب مجزا از ارقام 0 و 1 را ایجاد کند. یکی از ویژگیهای استفاده از کد BCD معرفی هر رقم اعشاری توسط مجموعهای از 4 بیت باینری مشابه با اعداد هگزادسیمال است، بنابراین هر رقم دسیمال (0 تا 9) توسط یک کد باینری 4 بیتی نمایش داده خواهد شد.
کدهای BCD و اعداد هگزادسیمال کاملا مشابه نیستند. در حالی که یک عدد هگزادسیمال 4 بیتی، میتواند تا عدد F16 معادل عدد دسیمال 15 (1111 باینری) را تولید کند، یک کد BCD میتواند تا عدد 1001 دسیمال یا باینری را تولید کند.
با وجود اینکه یک مجموعه 4 رقم باینری میتواند حداکثر 16 (2 به توان 4) ترکیب عددی را تولید کند، در سیستم شمارش BCD شش ترکیب باینری (1010)، (1011)، (1100)، (1101)، (1110)و (1111) به عنوان اعداد ممنوعه طبقهبندی میشوند و استفاده از آنها مجاز نخواهد بود.
مزیت اصلی استفاده از کد BCD فراهم کردن امکان تبدیل اعداد باینری و دسیمال به روشی ساده خواهد بود. با این حال عدم استفاده این کد از ارقام (1010 باینری) معادل 10 دسیمال تا رقم (1111 باینری) معادل 15 دسیمال، یکی از نقطه ضعفهای این روش است. با این وجود کد BCD کاربردهای بسیار مهمی به ویژه در نمایشگرهای دیجیتال دارد.
در سیستم شمارهگذاری BCD، هر رقم از اعداد دسیمال به 4 بیت تقسیم خواهد شد. هر رقم دسیمال توسط مقدار وزن باینری خود، به صورت مجموعههای 4 بیتی از رقم 0000 (صفر) تا 1001 (نه) را شامل خواهد شد.
به عنوان مثال، کد BCD معادل عدد دسیمال به صورت زیر معرفی خواهد شد.
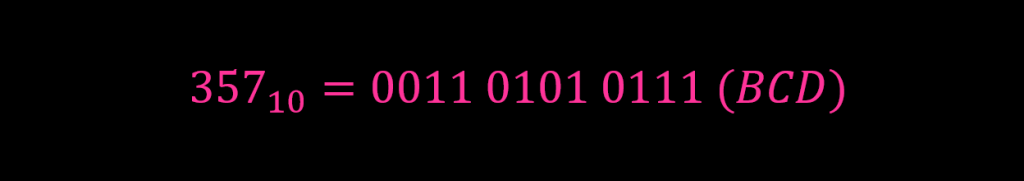
واضح است که، سیستم شماره گذاری BCD از کدگذاری وزنی استفاده میکند، و هر گروه 4 بیتی دارای وزن معینی از مقدار نهایی با توجه به جایگاه گروه خواهد بود. به بیان دیگر، BCD یک کد وزنی است و وزنهای معرفی شده در کد BCD عبارتند از 8,4,2,1. با توجه به اینکه روش کد BCD امکان نمایش اعداد دسیمال در قالب باینری را فراهم خواهد کرد، معمولا با نام کد 8421 نیز شناخته میشود.
ارائه کد BCD یک عدد دسیمال (Binary Coded Decimal Representation of a Decimal Number)
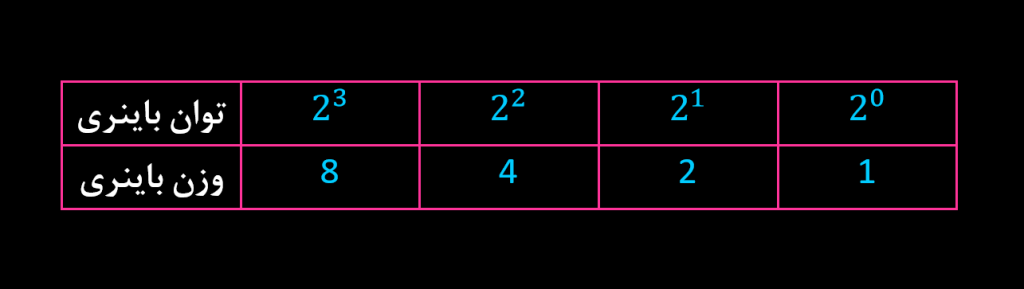
وزن هر رقم در سیستم اعداد دسیمال با حرکت به سمت چپ با ضریب 10 افزایش مییابد. همان طور که در جدول فوق نشان داده شده است، در سیستم اعداد BCD، وزن باینری هر رقم با ضریب 2 افزایش مییابد. به این ترتیب، وزن رقم اول معادل 1 (0^2)، رقم دوم وزنی معادل 2 (1^2)، رقم سوم 4 (2^2)، و وزن رقم چهارم برابر با 8 (3^2) خواهد بود.
رابطه بین اعداد دسیمال و ارقام BCD در جدول زیر ارائه شده است.
جدول صحت کد BCD
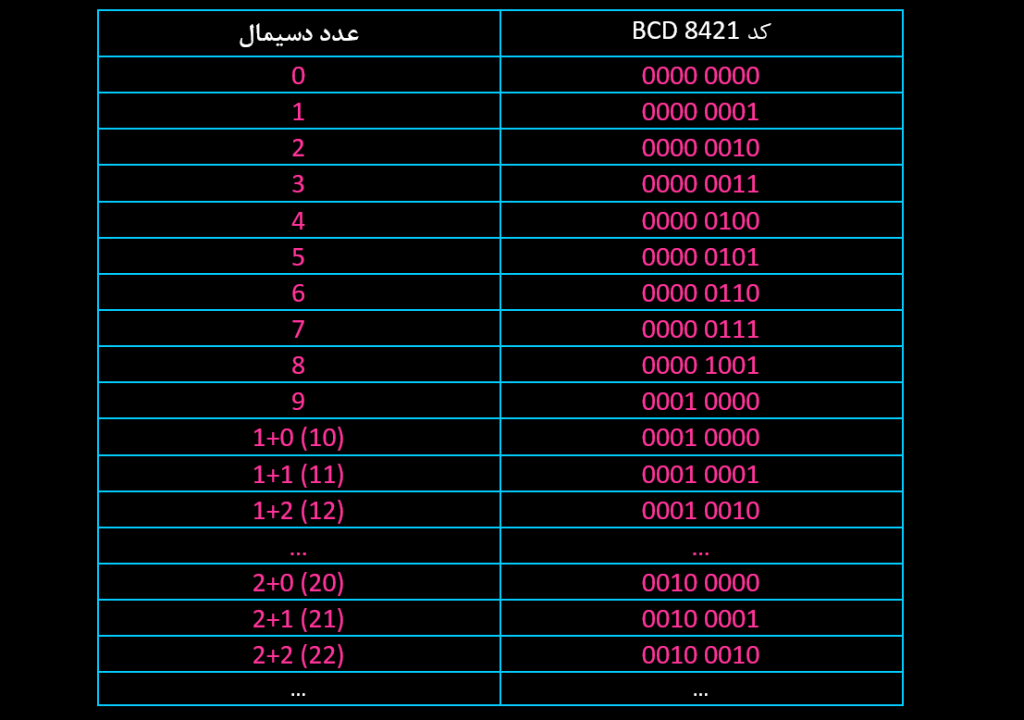
کاملا واضح است که کد BCD 8421 همان وزن هر رقم باینری است و هر رقم دسیمال توسط معادل باینری 4 بیتی آن نمایش داده خواهد شد.
تبدیل اعداد دسیمال به کد BCD (Decimal-to-BCD Conversion)
با توجه به توضیحات مطرح شده، تبدیل اعداد دسیمال به کد BCD مشابه با قوانین تبدیل اعداد هگزادسیمال به اعداد باینری خواهد بود. در ابتدا، ارقام وزندار عدد دسیمال را مشخص کرده و سپس معادل باینری هر رقم در قالب چهار بیتی معرفی میشوند. در نهایت معادل کد BCD 8421 عدد با کنار هم قرار دادن بیتهای مشخص شده بدست خواهد آمد.
مثال شماره یک
معادل کد BCD 8421 اعداد دسیمال (8579)، (572) و (85) با توجه به جدول بالا به صورت زیر محاسبه خواهد شد.
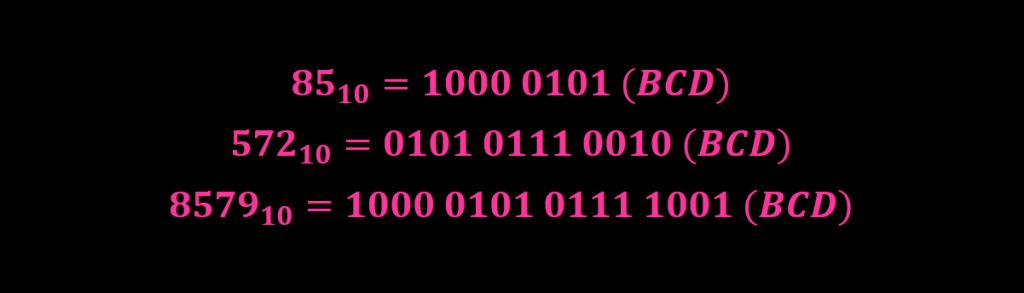
نکته مهم در تبدیل اعداد دسیمال به کد BCD توجه به معرفی ارقام در قالب 4 بیتی است. بنابراین درصورتی که معادل باینری رقمی کمتر از چهار بیت باشد، کافیست در سمت چپ رقم MSB به اندازه مورد نیاز صفر اضافه شود، تا قالب چهار بیتی مورد نظر ایجاد شود.
تبدیل کد BCD به عدد دسیمال (BCD-to-Decimal Conversion)
جهت تبدیل کد BCD به عدد دسیمال، کافیست عکس عملیاتهای فوق عمل شود. به این ترتیب ابتدا عدد باینری به مجموعههای چهار بیتی گروهبندی خواهد شد و سپس معادل دسیمال هر یک از ارقام گروههای باینری به ترتیب از سمت کم ارزش ترین بیت محاسبه میشود. به طور مشابه در صورت نیاز در سمت چپ عدد صفرهای اضافی جهت تشکیل گروههای چهار بیتی اضافه خواهد شد. برای مثال عدد باینری 110101 به صورت 0011 0101 و یا 35 دسیمال بیان میشود.
مثال شماره دو
معادل دسیمال، اعداد باینری 10100111000.101، 1000111، 1010، 1001 به صورت زیر محاسبه خواهد شد.
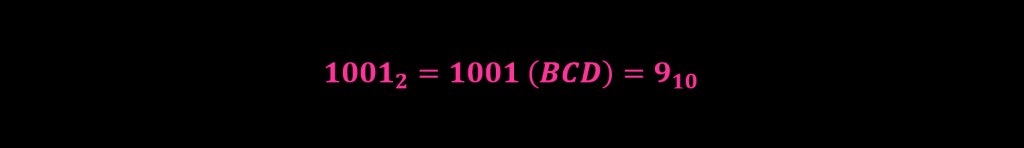
1010 باینری معادل با 10 دسیمال خواهد بود که یک عدد BCD غیر مجاز است.
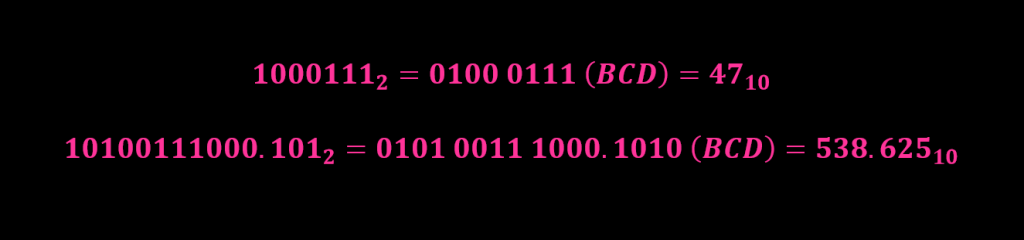
تبدیل عدد BCD به دسیمال یا اعداد دسیمال به کد BCD نسبتا راحت است و پیچیدگی خاصی ندارد؛ البته همواره باید توجه داشت که اعداد BCD در واقع اعداد دسیمال هستند و نه اعداد باینری، هرچند با بیتهای 0 و 1 نشان داده میشوند.
درک قالب BCD یک عدد دسیمال بسیار اهمیت دارد، زیرا سیستمهای مبتنی بر میکروپروسسور (microprocessor) که کاربردهای فراوانی دارند، مبتنی بر اعداد دسیمال هستند.
با این حال، در حالی که کد گذاری و رمز گشایی (decode) توسط کد BCD بسیار ساده است، اما روش مناسبی جهت ذخیره اعداد نخواهد بود. در رمز گذاری استاندارد (encoding) اعداد دسیمال به BCD 8421، همواره تعداد بیتهای لازم برای نمایش یک عدد دسیمال معین، بیشتر از تعداد بیتهای لازم جهت رمزگذاری باینری همان عدد خواهد بود.
برای مثال، معادل باینری یک عدد دسیمال سه رقمی (0 تا 999) تنها به 10 بیت (1111100111 باینری) نیاز خواهد داشت، در حالی که جهت نمایش کد BCD همان عدد به حداقل 12 بیت (0011 1110 0111 BCD) نیاز است.
همچنین، اعمال عملیاتهای محاسباتی روی اعداد BCD ممکن است مشکلاتی ایجاد کند. این اعداد نمیتوانند مقادیر بزرگتر از 9 را اختیار کنند، از این رو ممکن است حاصل جمع دو رقم اعشاری در این سیستم یک بیت کری (carry) ایجاد کند که باید به گروه چهار بیتی بعدی اضافه شود.
اگر حاصل جمع بیت (carry) با چهار بیت باینری کوچکتر مساوی 9 (1001) باشد، رقم BCD متناظر نیز صحیح خواهد بود. اما اگر این حاصل جمع بزرگتر از عدد 9 باشد، یک رقم BCD غیرمجاز تولید خواهد شد. بنابراین بهتر است که ابتدا اعداد BCD را به باینری تبدیل کرده، عملیات جمع را بر روی اعداد باینری انجام داده و در آخر نتیجهی به دست آمده مجددا در قالب BCD بیان شود.
با این وجود، استفاه از سیستم کد گذاری BCD در سیستمهای میکروالکترونیکی و سیستمهای کامپیوتری بسیار رایج است، به طور ویژه جهت نمایش یک یا چند رقم دسیمال بر روی LED یا LCD های هفت قسمتی که با نام (7-Segment) نیز شناخته میشوند. مدارهای مجتمع (integrated circuits) بسیار متنوعی نیز جهت دریافت ورودی BCD یا تولید خروجی BCD ارائه شدهاند.
آی سی 74LS90 یکی از رایج ترین و پرکاربردترین شمارنده و یا تقسیم کنندهی آسنکرون (asynchronous) با خروجی BCD است. این آیسی درای دو شمارنده مجزا تقسیم بر دو و تقسیم بر پنج است که از ترکیب هر دو میتوان یک شمارنده تقسیم بر ده تولید کرد. همچنین آی سی 74LS390 که نسخه دوگانه آی سی 74LS90 اصلی است و میتواند جهت تولید خروجیهای BCD با توجه به نیاز در مدارهای مختلف مورد استفاده قرار گیرد.
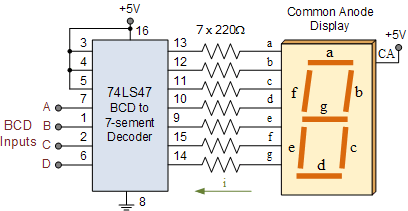
رایجترین آیسیهای رمزگذاری BCD (BCD encoded IC’s) عبارتند از 74LS47 و 74LS48 که کد BCD رمز گذاری شده را به کد 7-segment تبدیل خواهند کرد. آی سی 74LS48 یک کد BCD چهار بیتی را به کد 7-segment که جهت راه اندازی یک نمایشگر LED سون سگمنت لازم است، تبدیل خواهد کرد.
در حالی که عملکرد هر دو آیسی یکسان است، خروجی آیسی 74LS47 به صورت (active-low) خواهد بود و معمولا جهت راهاندازی نمایشگرهای (common-anode) استفاده خواهد شد، در حالی که خروجی آیسی 74LS48 به صورت (active-high) است و در راه اندازی نمایشگرهای (common-cathode) استفاده میشود.
خلاصه
کد BCD نمایش یک عدد دسیمال توسط گروههای چهار بیتی باینری است، به بیان دیگر هر رقم دسیمال یا صحیح با معادل باینری خود جایگزین خواهد شد. کد BCD از چهار بیت جهت نمایش 10 رقم دسیمال 0 تا 9 استفاده خواهد کرد.
بنابراین به عنوان مثال، جهت نمایش اعداد دسیمال در محدوده 0 تا 9 (یک رقم) 4 بیت معادل یک Nibble نیاز است، به طور مشابه برای نشان دادن اعداد دسیمال در بازه 0 تا 99 (دو رقم) به 8 بیت معادل یک بایت و اعداد دسیمال در بازه 0 تا 999 (سه رقمی) به 12 بیت نیاز است. تنها استفاده از یک بایت (8 بیت) امکان ذخیره سازی و یا نمایش ارقام BCD در بازه 00 تا 99 را فراهم خواهد کرد. این عدد دو رقمی با نام packed BCD نیز شناخته میشود.
کد BCD استاندارد معمولا با نام کد وزن دار BCD 8421 شناخته میشود، و اعداد 8، 4، 2 و 1 نشان دهنده وزن بیتهای مختلف با شروع از پر ارزش ترین (MSB) تا کم ارزش ترین بیت (LSB) است. به عبارت دیگر وزن هر یک از بیتهای کد BCD با توجه به موقعیت آن برابر با 8=3^2، 4=2^2 ، 2=1^2 و 1=0^2 است.
مهمترین مزیت کدهای BCD در مقایسه با سیستم اعداد باینری خالص، سریعتر بودن و کارآمدی بالای آنها در تبدیل اعداد دسیمال به باینری است. لازم به ذکر است که عدم به کارگیری شش ترکیب باینری چهار بیتی 10 تا 16 از گسترش کاربرد این کد جلوگیری خواهد کرد، اما همچنان در نمایشگرهای دسیمال کاربردهای بسیار مهمی دارد.







