علامت اعداد باینری (Signed Binary Numbers)
اعداد باینری علامت دار از MSB (پر ارزشترین بیت) به عنوان علامت بیت جهت نمایش محدوده مثبت یا منفی اعداد استفاده میکنند.
در ریاضیات، جهت نمایش اعداد مثبت (شامل عدد صفر) معمولا از نوشتن علامت + در سمت چپ اعداد صرف نظر میشود و به صورت اعداد بدون علامت نمایش داده میشوند.
با این حال، جهت نمایش اعداد منفی، علامت – در سمت چپ اعداد نوشته خواهد شد، تا تمایز بین اعداد مثبت و منفی مشخص شود. اعداد باینری علامت دار نیز از قواعد مشابه در ریاضیات پیروی میکنند.
این در حالی است که در مدارهای دیجیتال، هیچ پیش بینی ای جهت قرار دادن علامت مثبت یا منفی در کنار یک عدد تدارک دیده نشده است. زیرا عملکرد سیستمهای دیجیتال بر اساس اعداد باینری است که بهصورت صفر و یک نمایش داده میشوند. از کنار هم قرار گرفتن ارقام 0 و 1 در مدارهای میکروالکترونیک، مفهوم بیت (bit) پدید میآید. همچنین مجموعهای متشکل از 8 بیت با نام یک بایت (byte) و یا یک مجموعه 16 بیتی (2 بایت) با نام کلمه (word) شناسایی میشود.
با توجه به توضیحات مطرح شده در آموزشهای پیشین، یک عدد باینری 8 بیتی (یک بایت) میتواند مقادیری از 0 (0000 0000) تا 255 (1111 1111) را اخذ کند، به بیان دیگر ترکیب متفاوت و مختلف از بیتها، که یک بایت 8 بیتی منحصر به فرد را تشکیل میدهند. برای مثال عدد باینری بدون علامت 01001101 معادل مقدار دسیمال 77=1+4+8+64 خواهد بود. با این وجود سیستمهای دیجیتال و کامپیوترها نیز نیاز به استفاده از اعداد منفی مانند اعداد مثبت دارند.
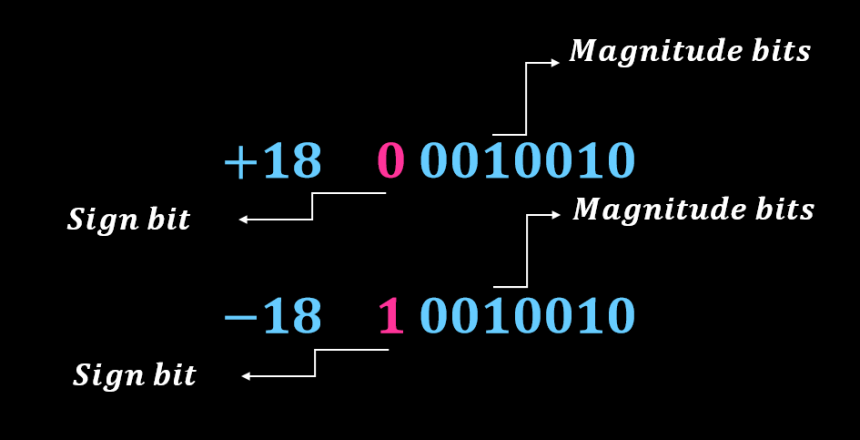
در ریاضیات، هر عدد شامل یک مقدار (بزرگی) و یک علامت است. علامت نمایانگر مثبت و یا منفی بودن عدد و مقدار نشان دهنده اندازه عدد خواهد بود. ارائه اعداد توسط این روش با نام (علامت-بزرگی) شناخته میشود، به این ترتیب اولین رقم از سمت چپ نماینده علامت عدد و باقی ارقام بزرگی عدد را معرفی خواهند کرد.
روش نمادگذاری علامت-بزرگی (Sign-magnitude) یکی از متداولترین روشها جهت نمایش اعداد مثبت و منفی است. بنابراین اعداد منفی با تغییر علامت عدد مثبت مربوطه بدست میآید، زیرا هر عدد مثبت یا بدون علامت دارای یک عدد متناظر با علامت منفی است. برای مثال 2+ و 2- و یا 10 و 10- .
با این حال نمایش علامت اعداد باینری در حالی که تنها شامل مقادیر 0 و 1 هستند، چالش آفرین خواهد بود، از طرفی هر عدد تنها یکی از دو علامت + و یا – را اخذ خواهد کرد.
بنابراین کافیست، از یک بیت واحد جهت تعیین و نمایش علامت یک عدد باینری به عنوان مثبت یا منفی استفاده شود. به این ترتیب جهت نمایش یک عدد باینری مثبت (n+) و عدد باینری منفی (n-)، اعداد با افزودن یک علامت معرفی خواهند شد.
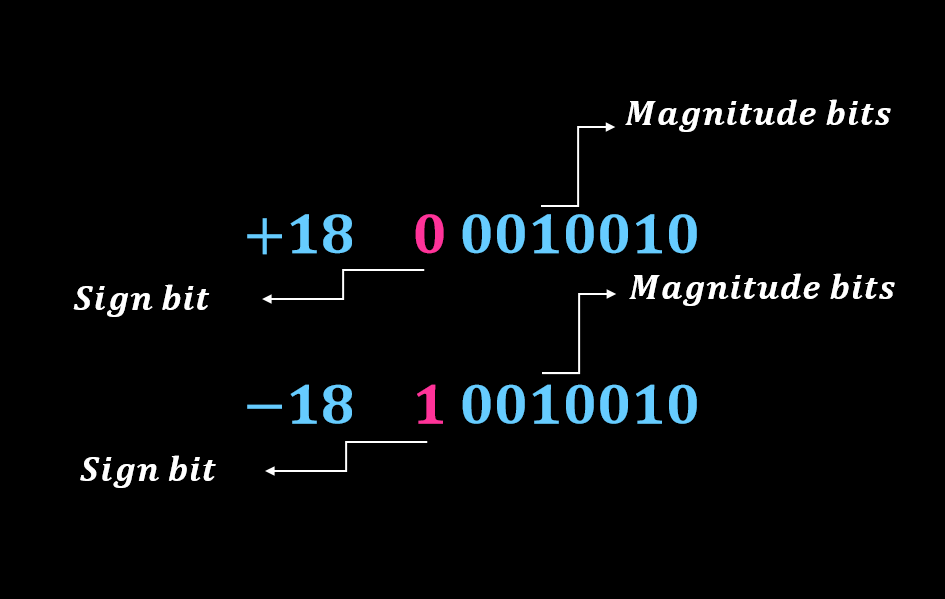
در اعداد باینری علامت دار، مهمترین بیت (MSB) به عنوان بیت معرف علامت استفاده خواهد شد. در صورتی که مقدار بیت علامت برابر 0 باشد، علامت عدد باینری مثبت خواهد بود و در صورتی که بیت علامت 1 باشد، علامت عدد باینری منفی است. بیتهای باقی مانده جهت نمایش بزرگی عدد باینری بدون علامت استفاده خواهند شد.
بنابراین در روش نمادگذاری علامت-بزرگی، مقادیر مثبت و منفی با تقسیم n بیت به دو قسمت حاصل میشود. یک بیت واحد جهت نمایش علامت و n-1 بیت به عنوان نمایندهی مقدار و بزرگی عدد خواهد بود. برای مثال، عدد دسیمال 53 را میتوان به صورت یک عدد باینری 8 بیتی علامت دار به صورت زیر معرفی کرد.
اعداد باینری علامت دار مثبت
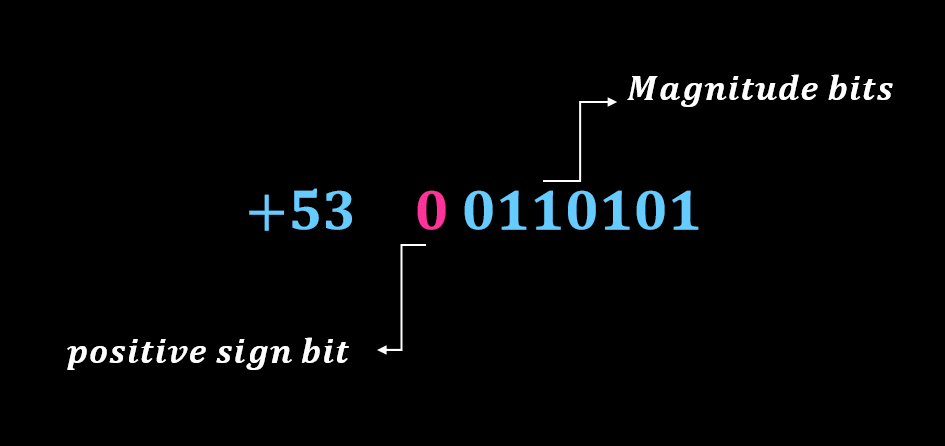
اعداد باینری علامتدار منفی

یکی از نقاط ضعف استفاده از این روش کاهش محدوده ارقام عدد باینری خواهد بود. به بیان دیگر با اعمال این روش، یک محدوده کامل از اعداد باینری بدون علامت n بیتی به یک عدد باینری علامتدار n-1 بیتی تبدیل خواهد شد.
برای مثال در صورتی که چهار بیت جهت معرفی یک عدد باینری علامت دار وجود داشته باشد (یک بیت علامت و سه بیت بزرگی عدد را مشخص خواهند کرد.)، در این صورت محدوده حقیقی اعدادی که در روش علامت-بزرگی نمایش داده میشوند به صورت زیر خواهد بود.
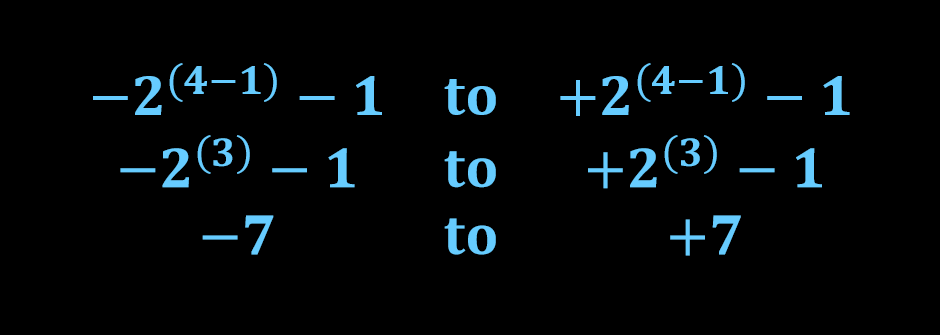
این در حالی است که، محدوده اعداد باینری چهار بیتی بدون علامت از 0 تا 15 معادل 0 تا F در دستگاه هگزادسیمال خواهد بود. اما با اعمال روش علامت-بزرگی محدوده نمایش اعداد به 7- تا 7+ کاهش یافته است. واضح است که اعداد باینری بدون علامت، محدوده اعداد بزرگتری را پوشش میدهند، زیرا در این اعداد MSB صرفا نشان دهنده علامت عدد نیست و یک رقم خواهد بود.
از دیگر چالشهای استفاده از روش علامت-بزرگی، اختصاص یک علامت صحیح برای عدد 0 خواهد بود. با استفاده از این روش میتوان دو علامت مختلف برای عدد صفر ایجاد کرد. یک صفر مثبت 0000 و یک صفر منفی 1000 این در حالی است که هر دو نمایش دارای اعتبار خواهد بود، بنابراین انتخاب علامت عدد صفر از دیگر مشکلات این روش است.
مثال شماره یک
با استفاده از روش علامت-بزرگی مقادیر دسیمال زیر، به صورت اعداد باینری علامتدار ارائه خواهند شد.

جهت نمایش عدد باینری 4 ، 6 و 8 و 16 و 32 بیتی، تمام بیتها باید دارای مقدار باشند، از این رو از عدد 0 جهت پر کردن فاصله موجود بین بیت علامت در سمت چپ و نخستین بیت دارای مقدار بالا (یک) استفاده خواهد شد.
روش علامت-بزرگی یک روش ساده جهت درک مفهوم اعداد باینری علامتدار است، عملکرد این روش مشابه با عملکرد سیستم اعداد اعشاری (مبنای 10) در ریاضیات است.
با این حال استفاده از روش علامت- بزرگی میتواند منجر به تولید یک مقدار باینری مشابه توسط دو الگوی توزیع بیتی متفاوت شود. برای مثال هر دو الگوی باینری 0000 و 1000 نماینده عدد 0+ و 0- به عنوان یک عدد باینری چهار بیتی هستند. وجود دو نمایش متفاوت برای صفر (یک صفر مثبت و یک صفر منفی) موجب پیچیدگیهای زیادی در سیستمهای دیجیتالی خواهد شد.
روش مکمل 1 برای عدد باینری علامتدار
مکمل 1 روش دیگری جهت نمایش اعداد باینری منفی در سیستم اعداد باینری علامتدار است. در این روش اعداد مثبت که با نام اعداد غیر مکمل شناسایی خواهند شد بدون تغییر باقی خواهند ماند.
اعداد منفی با استفاده از مکمل 1 (معکوس) اعداد مثبت ایجاد خواهند شد. از آنجا که اعداد مثبت همیشه با 0 آغازمی شوند، عدد مکمل همیشه با 1 آغاز میشود که نشاندهنده یک عدد منفی است.
مکمل 1 یک عدد باینری منفی، معادل مکمل 1 همتای مثبت آن عدد خواهد بود. بنابراین کافیست مقدار هر بیت با مقدار مجاز دیگر جایگزین شود. به بیان دیگر جهت تعیین مکمل 1 یک عدد باینری کافیست به ترتیب هر بیت با مقدار 0 به 1 و هر بیت با مقدار 1 به 0 تغییر داده شود. برای مثال مکمل 1 عدد باینری 10010100 با تبدیل ارقام 1 به 0 و همچنین ارقام 0 به 1 برابر با عدد 01101011 خواهد بود.
استفاده از اینورترها (Inverters) یکی از سادهترین روشها جهت یافتن مکمل 1 یک عدد باینری علامتدار، در زمان ساخت مدارهای محاسبات باینری و یا مدارهای رمزگشایی منطقی (logic decoder circuits) است. اینورتر به صورت طبیعی یک تولید کننده مکمل 1 در مدار است، که میتواند جهت محاسبه مکمل 1 هر عدد باینری به صورت موازی در مدار الکتریکی مورد استفاده قرار گیرد.
مکمل 1 با استفاده از اینورتر
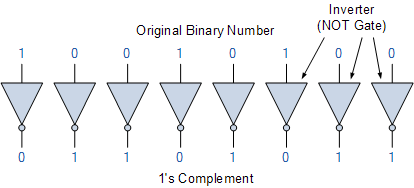
با توجه به توضیحات فوق، جهت یافتن مکمل 1 یک عدد باینری N کافیست بیتهای 1 به 0 و به صورت مشابه بیتهای 0 به 1 تبدیل شوند، تا معادل منفی عدد N تولید شود. همچنین مشابه با نمایش عدد باینری علامتدار در روش علامت-بزرگی در روش مکمل 1 نیز میتوان از نمادگذاری (1-n)2- و 1-(n-1)2+ استفاده کرد. برای مثال، یک نمایش 4 بیتی در قالب مکمل 1 میتواند جهت معرفی اعداد دسیمال در محدودهای از 7- تا 7+ همانند روش قبل دو نمایش برای صفر، به صورت 0000 (0+) و 1111 (0-) تولید کند.
جمع و تفریق با استفاده از مکمل 1
در ریاضیات، عملیات تفریق میتواند با روشهای متفاوتی بیان و در نهایت اجرا شود. برای مثال تفاوتی در حاصل A-B و B+A- وجود ندارد و هر دو تنها دو بیان مختلف برای یک مسئله هستند. بنابراین، پیچیدگیها و چالشهای تفریق دو عدد باینری را میتوان با تبدیل تفریق به جمع کاهش داد.
در آموزشهای پیشین اشاره شد که جمع اعداد باینری از الگوی مشابه با جمع در ریاضیات پیروی میکند، با این تفاوت که در سیستم اعداد باینری تنها دو عدد وجود دارد و بزرگترین رقم در این سیستم عدد 1 است (همانند رقم 9 که بزرگترین رقم در سیستم اعداد دسیمال است). بنابراین ترکیب احتمالی جمع اعداد باینری به صورت زیر بیان میشود.
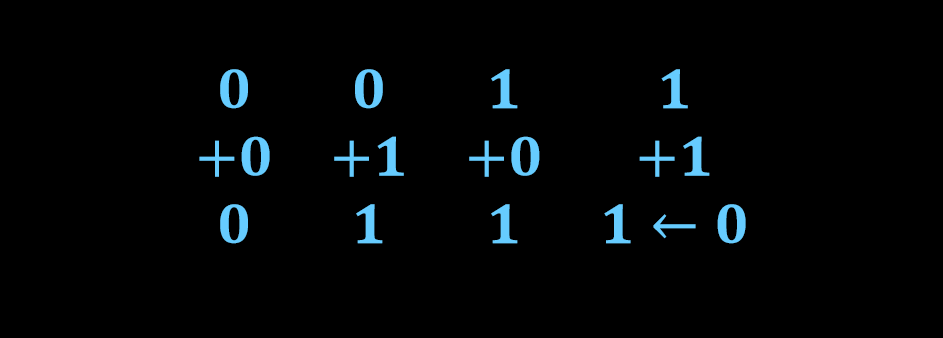
بر این اساس هرگاه دو عددی که با هم جمع میشوند هر دو مثبت باشند، با استفاده از جمع مستقیم (شامل علامت بیت و بزرگی بیت) به یکدیگر اضافه خواهند شد. به این ترتیب حاصل جمع بیتهای واحد مانند 0+0 و 0+1 و 1+0 برابر با 0 و یا 1 خواهد بود. به همین علت حاصل جمع دو بیت متفاوت (0+1 یا 1+0) برابر با 1 است. به صورت مشابه، حاصل جمع دو بیت مشابه (0+0 یا 1+1) برابر با 0 خواهد بود تا زمانی که جمع 1+1 ظاهر شود که نتیجه آن یک 0 و یک 1 اضافی خواهد بود.
تفریق دو عدد باینری
در ادامه با استفاده از روش مکمل 1 تفریق دو عدد باینری 115 و 27 در یک سیستم دیجیتالی 8 بیتی ارائه میشود.
در سیستم دسیمال (مبنای ده) حاصل تفریق 88=27-115 خواهد بود.
در گام نخست اعداد دسیمال به اعداد باینری تبدیل میشوند و سپس با افزودن صفرهای اضافه از یکسان بودن تعداد بیتهای اعداد اطمینان حاصل میشود. در نهایت آنها به اعداد 8 بیتی (یک بایت) تبدیل خواهند شد. بنابراین:
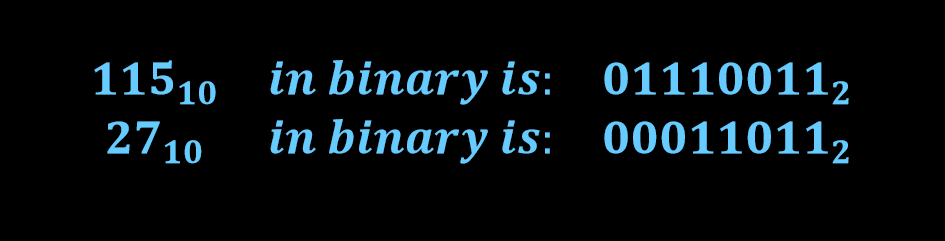
سپس مکمل عدد باینری منفی (27-) معادل عدد باینری 00011011 محاسبه خواهد شد، این در حالی است که عدد باینری اول 00011011 بدون تغییر باقی خواهد ماند. به این منظور با تغییر همه 1 ها به 0 و 0 ها به 1 مکمل عدد باینری 00011011 برابر با 11100100 خواهد بود.
حاصل جمع عدد باینری اول و مکمل عدد باینری دوم به صورت زیر ارائه میشود.
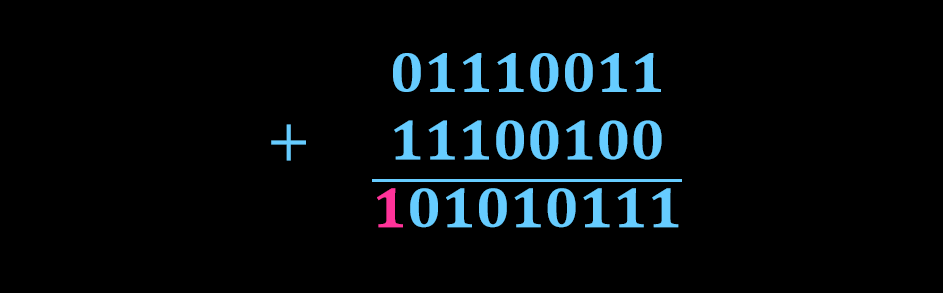
از آنجایی که سیستم دیجیتال باید با 8 بیت کار کند، تنها 8 رقم نخست برای ارائه پاسخ مجموع کافی خواهد بود و بیت آخر (بیت 9) را نادیده گرفته خواهد شد. این بیت با نام اورفلو (overflow) شناخته میشود. اورفلو زمانی رخ میدهد که مجموع ستون سمت چپ یک رقم اضافی تولید کند. بیت اضافی میتواند جهت محاسبات به سیستم دیجیتال بعدی منتقل شود و یا به طور کامل نادیده گرفته شود. اورفلو نشان دهنده پاسخ محاسبات عددی مثبت است در صورتی که اورفلو وجود نداشته باشد، عدد پاسخ، منفی خواهد بود.
حاصل محاسابات 8 بیتی فوق عدد (با صرف نظر از بیت اورفلو) خواهد بود. جهت تبدیل مجدد پاسخ مکمل به پاسخ حقیقی، عدد 1 به نتیجه مکمل اضافه خواهد شد.
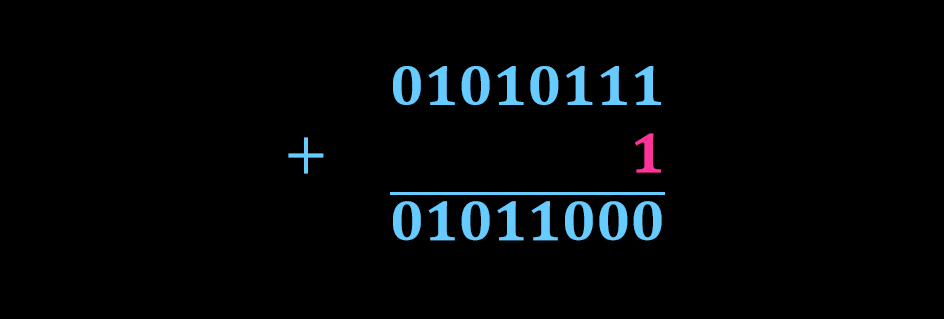
از این رو حاصل تفریق عدد 00011011 باینری معادل عدد دسیمال 27 از عدد 01110011 باینری معادل عدد دسیمال 115 با استفاده از روش مکمل 1 برابر با عدد 01011000 باینری معادل 88 دسیمال خواهد بود.
بنابراین حاصل جمع یا تفریق اعداد باینری علامت دار یا بی علامت، با استفاده از روش مکمل 1 به سادگی محاسبه خواهد شد. همچنین میتوان از آدرس باینری TTL 74LS83 یا 74LS283 جهت اعمال عملیاتهای جمع و تفریق دو عدد باینری علامت دار 4 بیتی و یا الحاق به هم برای تولید یک آدرس 8 بیتی کامل استفاده کرد.
روش مکمل 2 یک عدد باینری علامت دار
مکمل 2 روش دیگری مانند روش علامت-بزرگی و مکمل 1 جهت نمایش اعداد باینری منفی در سیستم اعداد باینری علامت دار است.
در روش مکمل 2 اعداد مثبت، دقیقا مشابه با اعداد باینری بدون علامت (مانند روش مکمل 1) خواهند بود. در حالی که، در این روش هر عدد منفی به صورت یک عدد باینری معرفی خواهند شد که حاصل جمع آن با معادل مثبت خود، برابر با صفر خواهد بود.
در روش مکمل 2، اعداد منفی با محاسبه مکمل 2 اعداد مثبت متناظر معرفی خواهند شد، همچنین انجام عملیات تفریق مشابه با روش قبل با تبدیل تفریق A-B به حاصل جمع (مکمل 2 B) +A امکان پذیر خواهد بود. به عبارت دیگر مکمل 2 همان مکمل 1+1 است.
مزیت اصلی روش مکمل 2 نسبت به مکمل 1، رفع مشکل ایجاد صفر مضاعف است و همچنین محاسبه مکمل 2 اعداد باینری بسیار سادهتر از روشهای دیگر است. بنابراین، انجام عملیاتهای محاسباتی به مراتب با معرفی اعداد در قالب روش مکمل 2 سادهتر خواهد بود.
برای مثال حاصل تفریق دو عدد 8 بیتی 115 و 27 با استفاده از روش مکمل 2 به صورت زیر ارائه خواهد شد.
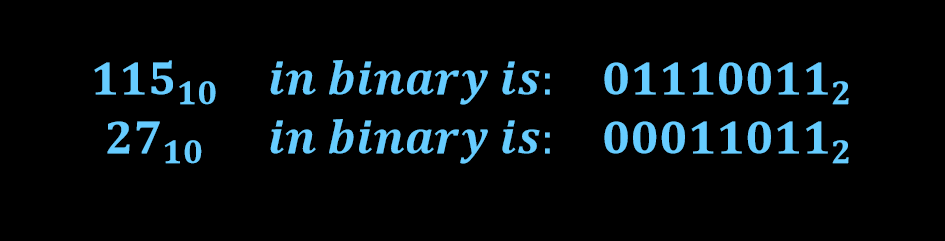
اعداد باینری فوق 8 بیتی هستند بنابراین 2 به توان 8 ترکیب از ارقام جهت نشان دادن مقادیر وجود دارند، که معادل باینری آن برابر با 100000000 باینری و یا عدد دسیمال 256 خواهد بود. حاصل مکمل 2 عدد دسیمال 27 به صورت زیر ارائه خواهد شد.
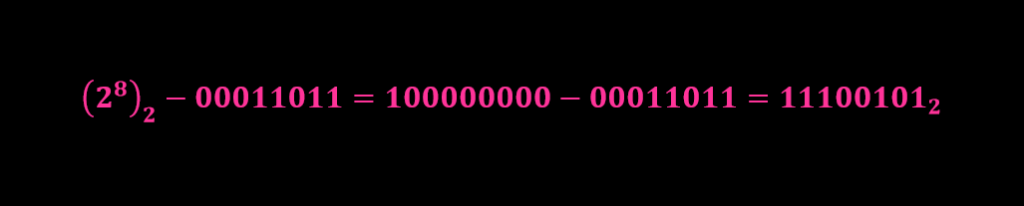
مکمل 2 یک عدد معادل با منفی همان عدد خواهد بود (محاسبه مکمل عدد 27+ آن را منفی خواهد کرد)، بنابراین جهت محاسبه تفریق دو عدد کافیست حاصل جمع آنها محاسبه شود، به عبارت دیگر 115+ (مکمل 2 عدد 27)
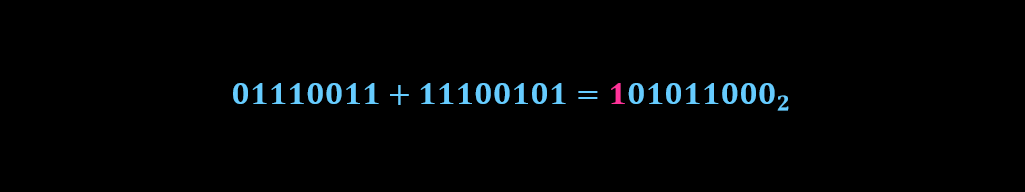
با توجه به توضیحات مطرح شده درمثال قبل، از بیت اورفلو (بیت 9) صرف نظر خواهد شد.
خلاصه اعداد باینری علامت دار
یکی از روشهای نمایش اعداد باینری منفی استفاده از با ارزشترین بیت (MSB) به عنوان بیت علامت است. در این صورت یک عدد باینری n بیتی علامت دار، از n-1 بیت جهت نمایش بزرگی عدد و 1 بیت به عنوان بیت علامت استفاده خواهد کرد.
به عنوان مثال، در یک عدد باینری 4 بیتی علامت دار تنها 3 بیت برای نمایش عدد وجود دارد. این در حالی است که در یک عدد باینری بدون علامت میتوان از تمام بیتهای موجود جهت نمایش عدد استفاده کرد.
معرفی اعداد باینری علامت دار به طور معمول با نام نمادگذاری علامت-بزرگی شناخته میشود، در صورتی که مقدار بیت علامت برابر با 0 باشد عدد مثبت و اگر برابر با 1 باشد عدد منفی خواهد بود. از طرفی هنگام انجام محاسبات بر روی اعداد باینری، استفاده از مکمل اعداد جهت معرفی عدد منفی بسیار سادهتر خواهد بود. در واقع روش مکمل جایگزینی برای نمایش اعداد باینری منفی خواهد بود. این سیستم کدینگ جایگزین، امکان تفریق اعداد با استفاده از عملیات جمع ساده را فراهم میکند.
با توجه به اینکه در روش علامت-بزرگی اعداد مثبت همواره با صفر شروع خواهند شد، بنابراین مکمل آنها نیز همواره با 1 شروع میشود که معرف عدد منفی خواهد بود.
مقایسه عدد باینری علامت دار 4 بیتی
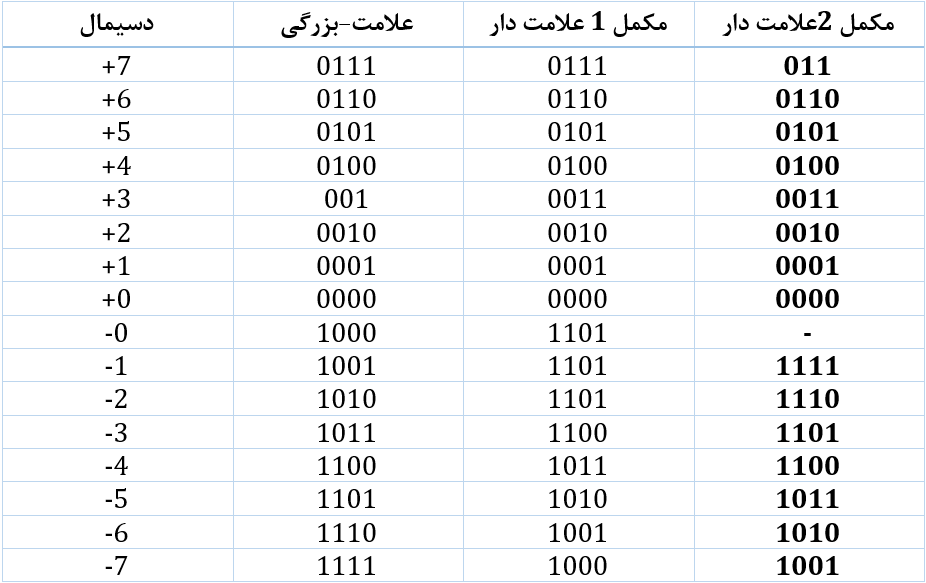
روشهای مکمل 1 و مکمل 2 امکان نمایش اعداد منفی در سیستم شمارهگذاری باینری را فراهم خواهند کرد. استفاده از روش مکمل 2 در محاسبات رایانهای جهت معرفی و مدیریت اعداد منفی بسیار رایج و مطلوب است. یکی از مشکلات استفاده از این روش جهت نمایش اعداد منفی، حذف بخشی از محدوده اعداد مثبت خواهد بود.





2 دیدگاه در “علامت اعداد باینری”
سپاس ، خیلی استفاده کردم. در فقط جدول بالایی چندتایی از اعداد اشتباه نوشته شده اند.
در جدول اخر یک سری اعداد اشتباه محاسبه شده اند.لطفا اصلاح کنید.