20 شهریور 1401

فیلتر Sallen-Key

بازدید: 730

20 شهریور 1401

فیلتر Sallen-Key

بازدید: 730

از مدار فیلتر سالن-کی (Sallen-Key) به عنوان یک بلوک اضافه‌شونده برای پیاده‌سازی فیلترهای اکتیو درجه بالاتر استفاده می‌شود.

طرح فیلتر Sallen-Key، یک توپولوژی فیلتر اکتیو مرتبه دوم است که می‌توانیم از آن به عنوان بلوک‌های اصلی برای پیاده‌سازی مدارهای فیلتر درجه بالاتر مانند پایین‌گذر (LPF)، بالاگذر (HPF) و میان‌گذر (BPF) استفاده کنیم.

همانطور که در این بخش فیلترها دیدیم، فیلترهای الکترونیکی، اعم از پسیو یا اکتیو، در مدارهایی استفاده می‌شوند که دامنه سیگنال فقط در محدوده محدودی از فرکانس‌ها مورد نیاز است. مزیت استفاده از طرح های فیلتر سالن-کی این است که پیاده‌سازی و درک آنها ساده است.

توپولوژی Sallen-Key یک طراحی فیلتر اکتیو مبتنی بر یک تقویت‌کننده عملیاتی غیر معکوس و دو مقاومت است، بنابراین یک طراحی منبع ولتاژ کنترل‌شده با ولتاژ (VCVS) با ویژگی‌های فیلتر همچون امپدانس ورودی بالا، امپدانس خروجی کم و پایداری خوب ایجاد می‌کند و به این ترتیب موجب می‌شود تا بخش‌های فیلتر Sallen-Key به صورت کسکود‌ شده در کنار هم قرار گیرند تا فیلترهای مرتبه بالاتری تولید کنند.

اما قبل از اینکه به طراحی و عملکرد فیلتر Sallen-Key نگاهی بیندازیم، اجازه دهید ابتدا ویژگی‌های یک مقاومت-خازن منفرد یا شبکه RC را زمانی که تحت طیف وسیعی از فرکانس‌های ورودی قرار می‌گیرد، یادآوری کنیم.

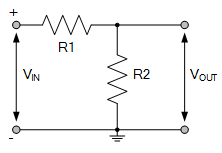
مقسم ولتاژ

وقتی که دو یا چند مقاومت در دو سر منبع ولتاژ DC در کنار هم قرار گرفته‌اند، مقادیر ولتاژی متفاوتی در دوسر هر مقاومت ایجاد خواهد شد و موجب ایجاد به اصطلاح یک مقسم ولتاژ یا شبکه تقسیم پتانسیل الکتریکی خواهد شد.

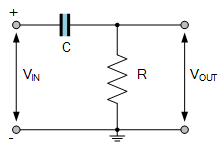
مدار اصلی نشان‌داده‌شده شامل دو مقاومت سری است که بر دو سر یک ولتاژ ورودی، V_IN، متصل شده‌اند.

قانون اهم به ما می‌گوید که افت ولتاژ یک مقاومت، حاصل جمع جریان عبوری ضربدر مقدار مقاومت آن است. بنابراین اگر دو مقاومت برابر باشند، افت ولتاژ دو سر هر دو مقاومت، R₁ و R₂ نیز برابر خواهد بود و به طور مساوی بین آنها تقسیم می‌شود.

افت ولتاژ ایجاد‌شده در مقاومت R₂ نشان‌دهنده ولتاژ خروجی V_OUT است و مقدار آن به نسبت دو مقاومت و ولتاژ ورودی بستگی دارد. بنابراین تابع انتقال برای این شبکه تقسیم ولتاژ ساده به صورت زیر ارائه می‌شود:

تابع انتقال مقسم ولتاژی مقاومتی

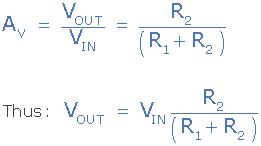
اما اگر ولتاژ ورودی را به منبع یا سیگنال AC و محدوده فرکانس آن را تغییر دهیم، برای ولتاژ خروجی V_OUT چه اتفاقی می‌افتد؟ در واقع هیچ چیز، زیرا مقاومت‌ها معمولا تحت تاثیر تغییرات فرکانس قرار نمی‌گیرند (به غیر از سیم‌پیچ‌ها). بنابراین پاسخ فرکانسی آنها صفر است و اجازه می‌دهند ولتاژهای AC با مقدار Irms²*R در دو سر مقاومت‌ها به همان اندازه که برای حالت پایدار DC است، ایجاد شود.

تقسیم کننده ولتاژ RC

همانطور که در زیر نشان داده شده است، اگر مقاومت R₁ را در بالا به خازن C تغییر دهیم، بر عملکرد تابع انتقال قبلی ما تاثیر می‌گذارد. از مقاله‌های بخش خازن‌ها می‌دانیم که یک خازن هنگامی که به منبع ولتاژ DC متصل می‌شود، مانند یک مدار باز عمل می‌کند.

بنابراین هنگامی که یک منبع تغذیه ثابت DC به V_IN متصل می‌شود، خازن به طور کامل پس از 5 ثابت زمانی (5T = 5RC) شارژ می‌شود و در این زمان هیچ جریانی از منبع تغذیه دریافت نمی‌کند. بنابراین جریانی از مقاومت R عبور نمی کند و افت ولتاژی در آن ایجاد نمی‌شود، بنابراین ولتاژ خروجی وجود ندارد. به عبارت دیگر، خازن‌ها پس از شارژ شدن، ولتاژهای DC حالت پایدار را مسدود می‌کنند.

اگر اکنون منبع ورودی را به یک ولتاژ سینوسی AC تغییر دهیم، ویژگی های این مدار RC ساده با مسدود شدن DC یا قسمت ثابت سیگنال کاملا تغییر می‌کند. بنابراین اکنون ما مدار RC را در حوزه فرکانس تجزیه و تحلیل می‌کنیم یعنی بخشی از سیگنال که به زمان بستگی دارد.

در یک مدار AC، یک خازن دارای ویژگی راکتانس خازنی X_C است، اما همچنان می‌توانیم مدار RC را به همان روشی که با مدارهای فقط مقاومت انجام دادیم، تحلیل کنیم، تنها تفاوت این است که امپدانس خازن اکنون به فرکانس بستگی دارد.

برای مدارها و سیگنال های AC، راکتانس خازنی (X_C) مقاومت در برابر عبور جریان متناوب از طریق خازن است که بر حسب اهم اندازه‌گیری می‌شود. راکتانس خازنی به فرکانس بستگی دارد، یعنی اینکه در فرکانس‌های پایین (ƒ ≅ 0) خازن مانند یک مدار باز عمل کرده و آنها را مسدود می‌کند. در فرکانس های بسیار بالا (ƒ ≅ ∞) خازن مانند یک اتصال کوتاه عمل کرده و سیگنال‌ها را مستقیما به صورت V_OUT = V_IN به خروجی انتقال می‌دهد. با این حال، جایی در بین این دو فرکانس، خازن دارای امپدانس داده شده توسط X_C است. بنابراین تابع انتقال مقسم ولتاژ به این صورت خواهد شد:

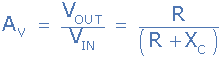
بنابراین تغییر در فرکانس باعث تغییرات در X_C می‌شود که باعث تغییر در مقدار دامنه ولتاژ خروجی می‌شود. مدار زیر را در نظر بگیرید.

مدار فیلتر RC

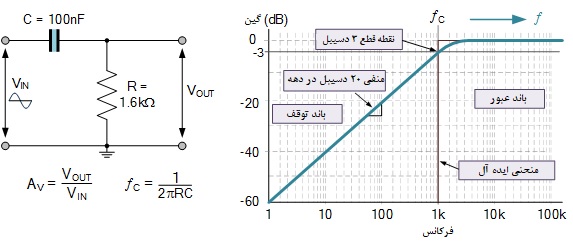
نمودار بالا، پاسخ فرکانسی این مدار ساده RC درجه 1 را نشان می‌دهد. در فرکانس‌های پایین، گین ولتاژ بسیار کم است، زیرا سیگنال ورودی توسط راکتانس خازن مسدود می‌شود. در فرکانس‌های بالا، گین ولتاژ بالا است (واحد) زیرا راکتانس باعث می‌شود که خازن به طور موثر به یک اتصال کوتاه در برابر این فرکانس‌های بالا تبدیل شود، بنابراین V_OUT = V_IN .

با این حال، یک نقطه فرکانس وجود دارد که در آن راکتانس خازن برابر با مقدار مقاومت است، یعنی به عبارت دیگر X_C = R و به آن نقطه «فرکانس بحرانی» یا به طور معمول فرکانس گوشه یا فرکانس قطع می‌گویند.

فرکانس گوشه f_C از آنجا که فرکانس قطع زمانی رخ می دهد که X_C=R، معادله استاندارد مورد استفاده برای محاسبه این نقطه فرکانس بحرانی به صورت زیر ارایه می‌شود:

معادله فرکانس قطع

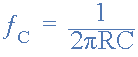
فرکانس قطع f_C جایی را مشخص می‌کند که مدار، در این مثال، از تضعیف یا مسدود کردن تمام فرکانس‌های زیر f_C تغییر حالت داده و شروع به عبور تمام فرکانس‌های بالای این نقطه f_C می‌کند. بنابراین مدار را «فیلتر بالاگذر» می‌نامند.

فرکانس قطع در جایی است که نسبت سیگنال ورودی به خروجی برابر با مقدار 707/0 است و هنگامی که به دسی بل تبدیل می شود برابر با منفی 3 دسی‌بل خواهد شد. این اغلب به عنوان نقطه 3 دسی‌بل پایین فیلتر شناخته می‌شود.

از آنجایی که راکتانس خازن به فرکانس مربوط می شود، یعنی راکتانس خازنی (X_C) با فرکانس اعمال شده نسبت عکس دارد، می‌توانیم معادله تقسیم ولتاژ بالا را برای به دست آوردن تابع انتقال این مدار فیلتر بالاگذر ساده RC تغییر دهیم.

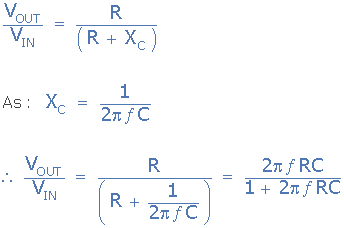
یکی از معایب اصلی فیلتر RC این است که دامنه خروجی همیشه کمتر از ورودی خواهد بود بنابراین هرگز نمی‌تواند بیشتر از واحد باشد. همچنین بارگذاری خارجی خروجی توسط طبقات یا مدارهای RC بیشتر بر خصوصیات فیلترها تاثیر خواهد داشت. یکی از راه‌های غلبه بر این مشکل، تبدیل فیلتر RC پسیو به «فیلتر RC اکتیو» با افزودن یک تقویت‌کننده عملیاتی به ساختار اولیه RC است.

با افزودن یک تقویت‌کننده عملیاتی، فیلتر RC پایه را می‌توان طوری طراحی کرد که مقدار مورد نیاز ولتاژ را در خروجی خود فراهم کند، بنابراین فیلتر را از یک تضعیف‌کننده به یک تقویت‌کننده تغییر می‌دهد. همچنین به دلیل امپدانس ورودی بالا و امپدانس خروجی کم یک تقویت‌کننده عملیاتی، از بارگذاری خارجی فیلتر جلوگیری می‌کند و باعث می‌شود بتوان آن را به راحتی در یک محدوده فرکانس وسیع، بدون تغییر در پاسخ فرکانسی طراحی‌شده تنظیم کرد.

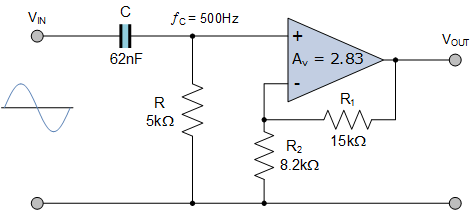
فیلتر ساده بالاگذر اکتیو RC زیر را در نظر بگیرید.

فیلتر بالاگذر اکتیو

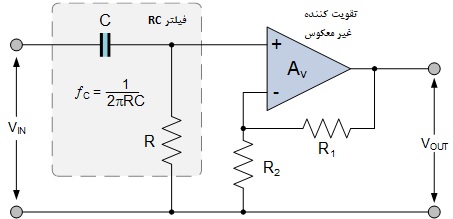
قسمت فیلتر RC مدار، پاسخی همچون شکل بالا دارد، یعنی با فرکانس قطعی که توسط مقادیر R و C تنظیم شده است، فرکانس‌های بالا را عبور می‌دهد اما فرکانس‌های پایین را مسدود می‌کند. تقویت‌کننده عملیاتی یا به اختصارآپ‌امپ به عنوان یک تقویت‌کننده غیرمعکوس ساخته شده است که با نسبت دو مقاومت R₁ و R₂، گین ولتاژی آن تنظیم می‌شود.

پس گین ولتاژ حلقه بسته A_V در باند عبور یک تقویت‌کننده عملیاتی غیر‌معکوس به صورت زیر داده می‌شود:

معادله گین ولتاژی تقویت کننده

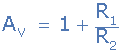
مثال 1- فیلتر RC

یک فیلتر بالاگذر اکتیو ساده درجه اول باید فرکانس قطع 500 هرتز و گین باند عبور 9 دسی‌بل داشته باشد. اجزای مورد نیاز را با فرض استفاده از تقویت‌کننده عملیاتی استاندارد 741 محاسبه کنید.

از بالا دیدیم که فرکانس قطع f_C با مقادیر R و C در مدار RC انتخاب‌کننده فرکانس تعیین می‌شود. اگر مقداری را برای مقاومت مثلا 5 کیلواهم فرض کنیم (هر مقدار معقولی قابل قبول است)، آنگاه مقدار C به صورت زیر محاسبه می‌شود:

اگر مقاومت را برابر با 5 کیلواهم انتخاب کنیم:

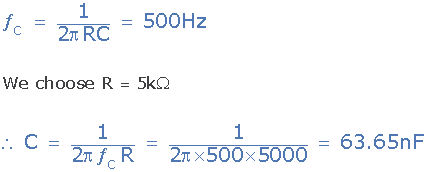
مقدار محاسبه شده 65/63 نانوفاراد برای خازن است، بنابراین نزدیکترین مقدار ترجیحی استفاده شده 62 نانوفازاد است. بهره فیلتر بالاگذر در ناحیه باند عبور باید مثبت 9 دسی‌بل باشد که معادل بهره ولتاژ A_V برابر با 83/2 است. یک مقدار دلخواه برای مقاومت فیدبک R₁ مثلا 15 کیلواهم فرض کنید، پس مقدار مقاومت R₂ برابر است با:

فرض می‌کنیم که مقاومت R₁ برابر با 15 کیلواهم باشد:

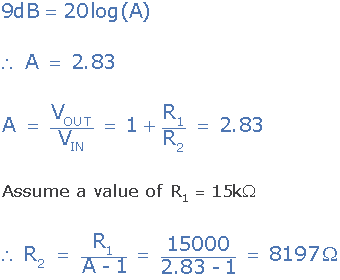
دوباره مقدار محاسبه شده 8197 اهم برای R₂ را می‌توان با نزدیکترین مقدار مقاومت یعنی 8200 اهم یا 2/8 کیلواهم تقریب بزنیم. پس مدار نهایی را برای مثال فیلتر بالاگذر اکتیو به این صورت مشخص می‌شود:

مدار فیلتر بالا‌گذر مثال 1

دیده‌ایم که می‌توان با استفاده از یک مقاومت و خازن که فرکانس قطع، نقطه f_C را تولید می‌کند، یک فیلتر بالاگذر مرتبه اول ساده ساخت که در آن دامنه خروجی ۳ دسی‌بل از دامنه ورودی پایین‌تر است. با افزودن طبقه دوم فیلتر RC به طبقه اول، می‌توانیم مدار را به یک فیلتر بالاگذر مرتبه دوم تبدیل کنیم.

فیلتر مرتبه دوم RC

ساده‌ترین فیلتر RC درجه دوم از دو بخش RC تشکیل شده است که در کنار هم کسکود شده‌اند. با این حال، برای اینکه این ساختار اولیه به درستی کار کند، امپدانس‌های ورودی و خروجی دو مرحله RC نباید بر عملکرد یکدیگر تاثیر بگذارند، یعنی باید هیچ اثری بر یکدیگر نداشته باشند.

مدار فیلتر بالاگذر مرتبه دوم

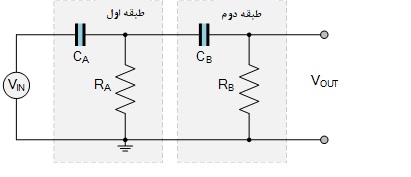
کسکود کردن یک طبقه فیلتر RC با مقادیر یکسان یا متفاوت یک طبقه RC دیگر کارایی خوبی ندارد زیرا هر مرحله متوالی، اثر بارگذاری بر مرحله قبلی دارد و هنگامی که طبقات RC بیشتری اضافه می‌شود، نقطه فرکانس قطع از آنچه طراحی شده یا مورد نیاز است دورتر می‌شود.

یک راه برای غلبه بر این مشکل برای طراحی فیلتر پسیو این است که امپدانس ورودی طبقه دوم RC حداقل 10 برابر بیشتر از امپدانس خروجی طبقه اول RC باشد. این یعنی مقادیر R_B = 10R₁ و C_B = C_A/10 در فرکانس قطع موجود باشد.

مزیت افزایش مقادیر اجزا با ضریب 10 این است که فیلتر درجه دوم حاصل، شیب تندتری در قسمت شیبدار یعنی 40 دسی‌بل در دهه نسبت به مراحل RC کسکود ایجاد می‌کند. اما اگر بخواهید فیلتر درجه 4 یا 6 طراحی کنید، محاسبه ده برابر ارزش اجزای قبلی می‌تواند زمان بر و پیچیده باشد.

یکی از راه‌های ساده برای کسکود کردن طبقات فیلتر RC که برای ایجاد فیلترهای درجه بالاتر با یکدیگر تعامل یا بارگذاری نمی‌کنند (نیازی به داشتن بخش‌های فیلتر یکسان نیست) که می‌توانند به راحتی تنظیم و طراحی شوند تا گین ولتاژی مورد نیاز را فراهم کنند، استفاده از طبقات فیلتر Sallen-Key است.

فیلتر‌های Sallen-Key

Sallen-Key یکی از متداول‌ترین ساختارهای فیلتر برای طراحی فیلترهای مرتبه اول و دوم است و به عنوان بلوک اصلی برای ایجاد فیلترهای مرتبه بالاتر استفاده می‌شود.

مزایای اصلی طراحی فیلتر سالن-کی عبارتند از:

سادگی و درک خوب از طراحی پایه
استفاده از تقویت‌کننده غیر‌معکوس برای افزایش گین
فیلتر‌های مرتبه اول و دوم به راحتی می‌توانند به صورت کسکود در کنار هم قرار بگیرند.
طبقات پایین‌گذر و بالاگذر می‌توانند با هم کسکود شوند
هر طبقه RC می‌تواند گین متفاوت داشته باشد.
یکی بودن اجزای تشکیل‌دهنده تقویت‌کننده‌ها و شبکه‌های RC
طبقات Sallen-Key درجه دوم نسبت به طبقات کسکود شده RC شیب قسمت شیب‌دار بیشتر و برابر با 40 دسی‌بل دارند.

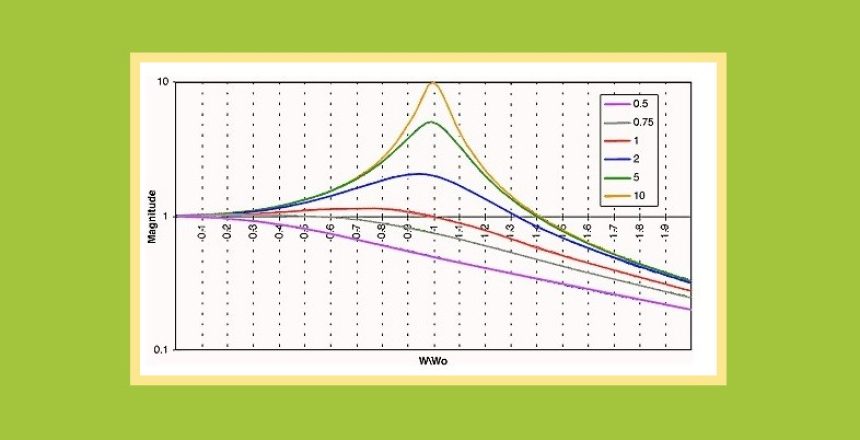
با این حال، محدودیت‌هایی برای طراحی فیلتر Sallen-Key وجود دارد، زیرا گین ولتاژ یا A_V و ضریب بزرگ‌نمایی یا Q به دلیل استفاده از تقویت‌کننده عملیاتی در طراحی سالن-کی، وابستگی زیادی دارند.

تقریبا هر مقدار Q بزرگتر از 5/0 را می‌توان ساخت زیرا با استفاده از یک ساختار غیر‌معکوس، گین ولتاژ یاA_V همیشه بزرگتر از 1 خواهد بود اما باید کمتر از 3 باشد در غیر این صورت ناپایدار می‌شود.

ساده‌ترین شکل طراحی فیلتر سلن-کی، استفاده از مقادیر برابر خازن و مقاومت است (اما نه اینکه مقادیر R و C با هم یکسان باشند) با تقویت‌کننده عملیاتی که به‌عنوان یک بافر با گین واحد ساخته شده‌است. توجه داشته باشید که مقاومت R_A دیگر به زمین متصل نیست، اما در عوض فیدبک مثبتی را برای تقویت‌کننده فراهم می‌کند.

مدار فیلتر بالاگذر Sallen Key

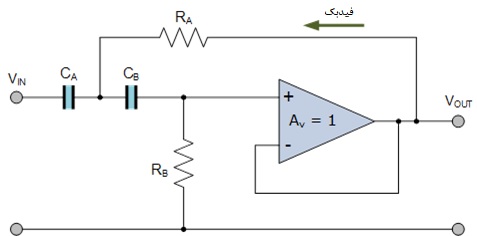
اجزای پسیو C_A، R_A، C_Bو R_B مدار درجه دوم انتخاب‌کننده فرکانس را تشکیل می‌دهند.

بنابراین در فرکانس‌های پایین، خازن‌های C_A و C_B به صورت مدار باز ظاهر می‌شوند، بنابراین سیگنال ورودی مسدود می‌شود و در نتیجه خروجی وجود ندارد. در فرکانس‌های بالاتر، C_A و C_B در سیگنال ورودی سینوسی به‌عنوان اتصال کوتاه ظاهر می‌شوند، بنابراین سیگنال مستقیما به خروجی بافر می‌شود.

با این حال، همانطور که در بالا ذکر شد، در اطراف نقطه فرکانس قطع، امپدانس C_A و C_B همان مقدار R_A و R_B خواهد بود، بنابراین فیدبک مثبت تولید شده از طریق C_B باعث ایجاد گین ولتاژی و افزایش بزرگنمایی سیگنال خروجی Q می‌شود.

از آنجایی که ما اکنون دو مجموعه از شبکه‌های RC داریم، معادله بالا برای فرکانس قطع برای فیلتر سالن-کی نیز اصلاح می شود:

اگر دو خازن سری C_A و C_B برابر باشند (C_A = C_B = C) و دو مقاومت R_A و R_B نیز به این صورت برابر شوند، (R_A = R_B = R) معادله فوق به معادله فرکانس قطع اصلی ساده می‌شود:

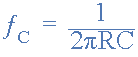
از آنجایی که تقویت‌کننده عملیاتی به عنوان یک بافر گین واحد ساخته می‌شود، یعنی A = 1 فرکانس قطع ƒ_C و Q کاملا مستقل از یکدیگر هستند و با طراحی فیلتر ساده‌تری روبرو خواهیم بود. پس ضریب بزرگنمایی Q به صورت زیر محاسبه می‌شود:

بنابراین برای ساختار بافر با گین واحد، بهره ولتاژ (A_V) مدار فیلتر برابر با 0.5 یا منفی 6 دسی‌بل (بیش از حد میرا) در نقطه فرکانس قطع است، و ما انتظار داشتیم که چنین اتفاقی بیفتد زیرا پاسخ یک فیلتر درجه دوم است پس

0.7071*0.7071 = 0.5

-3dB*-3dB = -6dB

با این حال، از آنجایی که مقدار Q ویژگی‌های پاسخ فیلتر را تعیین می‌کند، انتخاب مناسب دو مقاومت فیدبک تقویت‌کننده عملیاتی، R₁ و R₂، به ما این امکان را می‌دهد که گین باند عبور مورد نیاز A را برای ضریب بزرگنمایی انتخاب‌شده Q ایجاد کنیم.

توجه داشته باشید که برای توپولوژی فیلتر سلن-کی، انتخاب مقدار A بسیار نزدیک به حداکثر مقدار 3، به مقادیر Q بالا منجر می‌شود. مقدار Q بالا طراحی فیلتر را نسبت به تغییرات تلرانس در مقادیر مقاومت‌های فیدبک R₁ و R₂ حساس می‌کند.

به عنوان مثال، تنظیم بهره ولتاژ روی 2.9 (A = 2.9) باعث می‌شود که مقدا Q 10 باشد (1/(3-2.9)) بنابراین فیلتر در اطراف ƒ_C بسیار حساس می‌شود.

پاسخ فیلتر Sallen Key

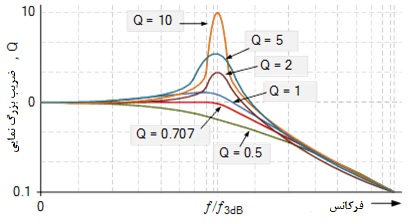
پس می‌بینیم که هرچه مقدار Q کمتر باشد، طراحی فیلتر سالن کی پایدارتر خواهد بود. در حالی که مقادیر بالای Q می‌تواند طراحی را ناپایدار کند، گین‌های بسیار بالا که Q منفی ایجاد می‌کند، منجر به نوسان می‌شود.

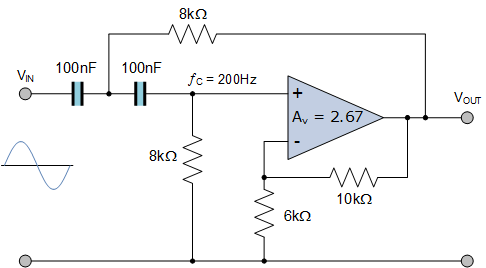
مثال 2- فیلتر سالن-کی

یک مدار سلن-کی بالاگذر درجه دوم با این مشخصات طراحی کنید

برای ساده‌سازی محاسبات ریاضی فرض می‌کنیم که دو خازن سری C_A و C_B برابرند و مقادیر دو مقاومت R_A و R_B نیز یکسان هستند (C_A=C_B=C & R_A=R_B=R).

مقدار خازن را برابر با 100 نانوفارد انتخاب می‌کنیم:

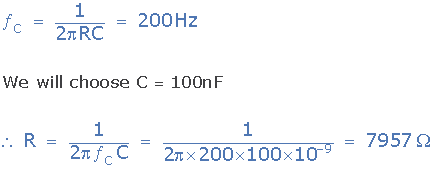
مقدا مقاومت محاسبه شده برابر با 7957 اهم است که با نزدیکترین مقدار واقعی یعنی 8 کیلواهم تقریب می‌زنیم.

برای Q=3 گین به این صورت محاسبه می‌شود:

اگر گین برابر با 667/2 باشد، پس نسبت خواهد بود.

اگر مقدار R₁ را برابر با 10 کیلواهم در نظر بگیریم:

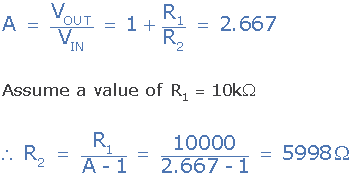
مقدار مقاومت محاسبه شده برابر با 5998 اهم می‌باشد که نزدیک‌ترین مقدار که 6 کیلواهم است را انتخاب می‌کنیم. با این محاسبات مدار نهایی فیلتر سلن-کی بالاگذر مثال 2 به این صورت خواهد بود:

فیلتر بالاگذر سالن کی مثال 2

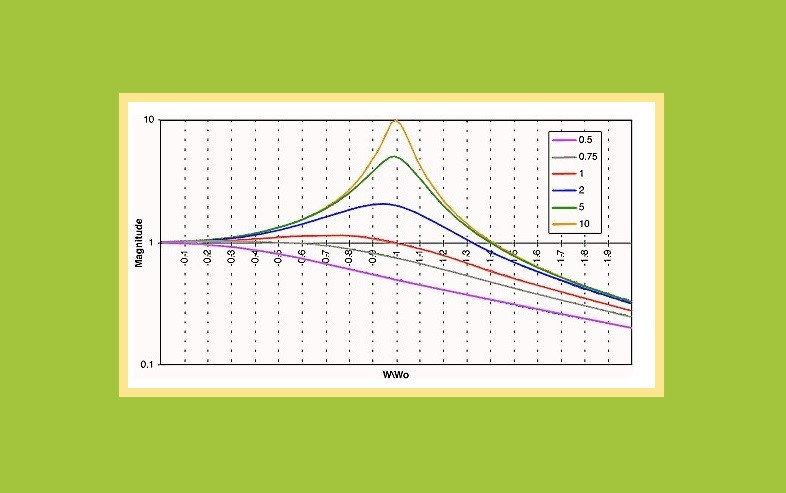
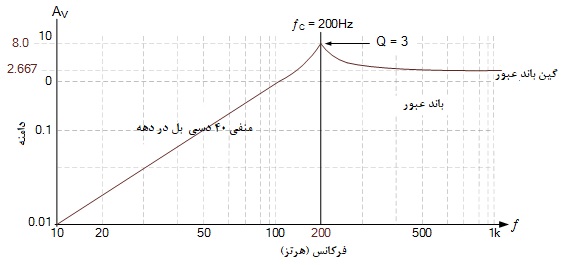
پس با فرکانس قطع یا گوشه 200 هرتز، گین باند عبور 667/2 و حداکثر گین ولتاژی در فرکانس قطع به دلیل Q=3، می‌توانیم مشخصات چنین فیلتر سلن-کی بالاگذر درجه دوم را به صورت نمودار بد زیر نمایش دهیم.

نمودار بد فیلتر Sallen Key

خلاطه فیلتر Sallen-Key

در این مقاله دیدیم که ساختار سالن-کی که به عنوان مدار منبع ولتاژ کنترل شده با ولتاژ (VCVS) نیز شناخته می‌شود، پرکاربردترین توپولوژی فیلتر است که عمدتا به این دلیل است که تقویت‌کننده عملیاتی مورد استفاده در طراحی آن می‌تواند با یک بافر افزایش واحد یا با یک تقویت‌کننده غیر معکوس ساخته شود.

پیکربندی اصلی فیلتر Sallen-Key را می‌توان برای اجرای پاسخ های فیلتر مختلف مانند باترورث، چبیشف یا بسل با انتخاب صحیح شبکه فیلتر RC استفاده کرد. بیشتر مقادیر عملی R و C را می‌توان با یادآوری اینکه برای یک نقطه فرکانس قطع خاص، مقادیر R و C نسبت معکوس دارند استفاده کرد. یعنی با کوچکتر شدن مقدار R، C بزرگتر می‌شود و بالعکس.

Sallen-Key یک طراحی فیلتر مرتبه دوم است که می‌تواند با سایر طبقات RC برای ایجاد فیلترهای مرتبه بالاتر کسکود شود. طبقات مختلف فیلتر لازم نیست یکسان باشند، اما هر کدام می‌توانند فرکانس قطع یا گین متفاوتی داشته باشند. به عنوان مثال، کنار هم قرار دادن یک طبقه پایین‌گذر و یک طبقه بالا‌گذر برای ایجاد یک فیلتر میان‌گذر Sallen-Key.

در اینجا به طراحی فیلتر بالاگذر Sallen-Key پرداختیم، اما قوانین مشابه برای طراحی فیلتر پایین‌گذر Sallen-Key نیز اعمال می‌شود. گین ولتاژ یا A_V تقویت‌کننده پاسخ آن را تعیین می‌کند. گین ولتاژ توسط دو مقاومت تقسیم‌کننده ولتاژ، R₁ و R₂ از پیش تنظیم شده است. به یاد داشته باشید که گین ولتاژ باید همیشه کمتر از 3 باشد در غیر این صورت، مدار فیلتر ناپایدار می‌شود و نوسان می‌کند.