پاسخ فرکانسی تقویت کننده یا فیلتر نشان میدهد که چگونه بهره خروجی به سیگنالهای ورودی در فرکانسهای مختلف پاسخ میدهد.
تقویت کنندهها و فیلترها از مدارهای الکترونیکی پرکاربرد و دارای خواص تقویت و فیلتراسیون هستند، که نام آنها نیز از این رو انتخاب شده است.
تقویت کنندهها بهره تولید میکنند، در حالی که فیلترها دامنه و یا مشخصات فاز سیگنال الکتریکی را نسبت به فرکانس آن تغییر میدهند. از آنجا که این تقویت کنندهها و فیلترها از شبکههای مقاومتی، سلفی یا خازنی (RLC) در طراحی خود استفاده میکنند، بین استفاده از این اجزای راکتیو و مشخصه پاسخ فرکانسی مدار رابطه مهمی وجود دارد.
هنگام کار با مدارهای AC فرض بر این است که آنها با فرکانس ثابت کار میکنند، به عنوان مثال ۵۰Hz یا ۶۰Hz. اما پاسخ یک مدار AC خطی را میتوان با یک سیگنال ورودی AC یا سینوسی با اندازه ثابت اما با فرکانس متغیر، مانند آنچه در مدارهای تقویت کننده و فیلتر یافت میشود، بررسی کرد. این امر اجازه میدهد تا چنین مدارهایی با استفاده از تحلیل پاسخ فرکانسی مورد مطالعه قرار گیرند.
پاسخ فرکانسی یک مدار الکتریکی یا الکترونیکی به ما اجازه میدهد تا دقیقا ببینیم چگونه بهره خروجی (معروف به پاسخ دامنه) و فاز (معروف به پاسخ فاز) در یک فرکانس خاص یا در طیف وسیعی از فرکانسهای مختلف، از ۰Hz (DC) تا هزاران مگا هرتز (MHz)، بسته به ویژگیهای طراحی مدار، تغییر میکند.
به طور کلی، تجزیه و تحلیل پاسخ فرکانسی یک مدار یا سیستم با رسم بهره آن، یعنی نسبت اندازه سیگنال خروجی آن به سیگنال ورودی، نسبت به مقیاس فرکانسی که انتظار میرود مدار یا سیستم در آن کار کند، نشان داده میشود. پس آگاهی از بهره (یا افت) مدار در هر نقطه فرکانس به ما کمک میکند تا بفهمیم که مدار چقدر خوب (یا بد) میتواند سیگنالها با فرکانسهای مختلف را تشخیص دهد.
پاسخ فرکانسی یک مدار وابسته به فرکانس معین را میتوان به صورت نموداری گرافیکی از بزرگی (بهره) نسبت فرکانس (f) نمایش داد. محور فرکانس افقی معمولا در مقیاس لگاریتمی ترسیم میشود، در حالی که محور عمودی نشان دهنده ولتاژ خروجی یا بهره، معمولا در مقیاس خطی با تقسیم بندی دسیمال ترسیم میشود. از آنجا که بهره یک سیستم میتواند مثبت یا منفی باشد، بنابراین محور y نیز میتواند دارای مقادیر مثبت و منفی باشد.
در الکترونیک، لگاریتم یا به اختصار «log» توان ریاضی است که باید به عدد پایه اعمال شود تا عدد اصلی به دست آید. پس در نمودار بود، مقیاس محور x لگاریتمی در تقسیم بندی log10 مدرج میشود، بنابراین هر دهه فرکانس (به عنوان مثال، ۰/۰۱، ۰/۱، ۱، ۱۰، ۱۰۰، ۱۰۰۰ و غیره) با فواصل مساوی بر روی محور x قرار داده میشود. عمل مخالف لگاریتم، آنتی لگاریتم یا «antilog» نام دارد.
نمایش گرافیکی منحنیهای پاسخ فرکانسی نمودار بود (Bode Plot) نامیده میشود و به این ترتیب گفته میشود که نمودارهای بود عموما گرافهای نیمه لگاریتمی هستند، زیرا یک مقیاس (محور x) لگاریتمی و مقیاس دیگر (محور y) خطی است (نمودار log-lin یا لگاریتمی-خطی).
منحنی پاسخ فرکانس
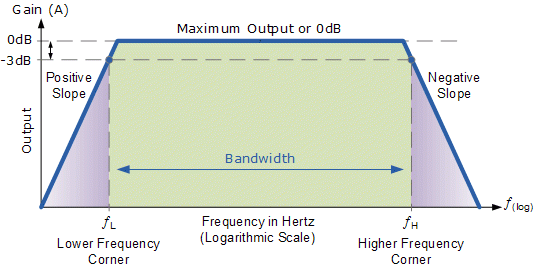
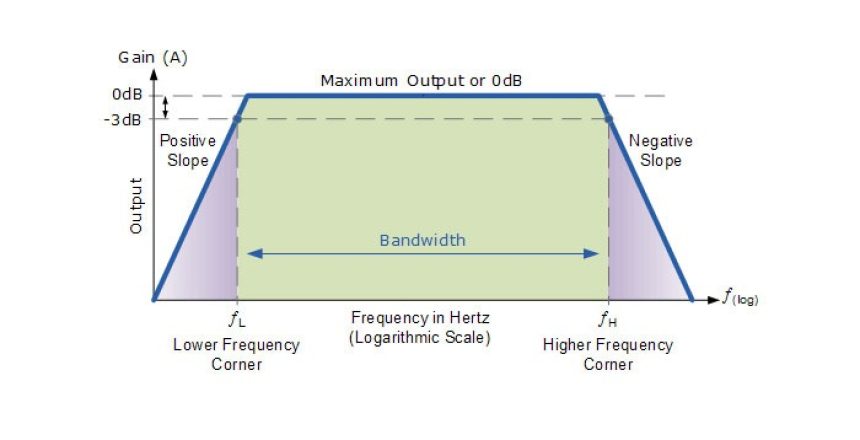
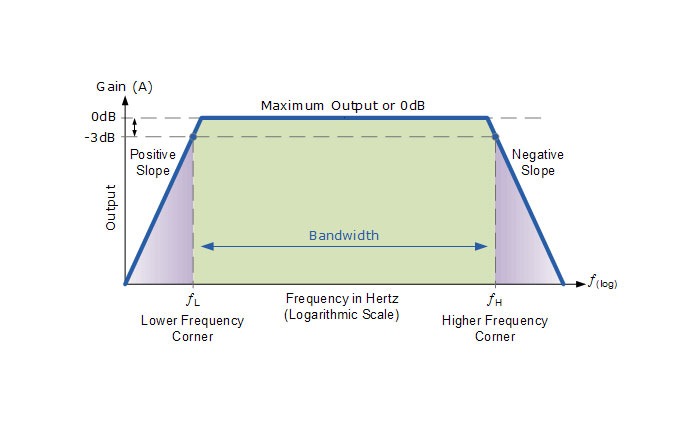
پس میبینیم که پاسخ فرکانسی هر مدار، تغییر رفتار آن با تغییرات در فرکانس سیگنال ورودی است، زیرا باند فرکانسی را نشان میدهد که در آن خروجی (و بهره) نسبتا ثابت باقی میماند. محدوده فرکانسهای بزرگ یا کوچک بین fL و fH پهنای باند مدار نامیده میشود. بنابراین از این طریق میتوانیم در یک نگاه بهره ولتاژ (بر حسب dB) را برای هر ورودی سینوسی در یک محدوده فرکانس معین تعیین کنیم.
همانطور که ذکر شد، نمودار بود نمایش لگاریتمی پاسخ فرکانس است. اکثر تقویت کنندههای صوتی مدرن، در طول کل طیف فرکانسهای صوتی از ۲۰Hz تا ۲۰kHz، دارای پاسخ فرکانسی یکنواخت، مانند شکل بالا هستند. این محدوده فرکانس برای تقویت کننده صوتی، پهنای باند آن (BW) نام دارد و در درجه اول با پاسخ فرکانسی مدار تعیین میشود.
نقاط فرکانس fL و fH به ترتیب مربوط به فرکانس گوشه یا قطع پایین و بالا هستند که در فرکانسهای پایینتر و بالاتر از آنها بهره مدار کاهش مییابد. این نقاط روی منحنی پاسخ فرکانس معمولا به عنوان نقاط ۳dB- (دسی بل) شناخته میشوند. بنابراین پهنای باند به شرح زیر به دست میآید:
دسی بل (dB) که یک دهم یک بل (B) است، یک واحد غیر خطی متداول برای اندازه گیری بهره میباشد که در محور y رسم میشود و به صورت ۲۰log10(A) تعریف میشود که در آن A بهره دسیمال است. صفر دسی بل (۰dB) مربوط به یک تابع بزرگی واحد است که حداکثر خروجی را نمایش میدهد. به عبارت دیگر، ۰dB زمانی اتفاق میافتد که Vout=Vin، زیرا در این سطح فرکانس تضعیف وجود ندارد و به صورت زیر داده میشود:
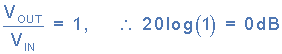
از نمودار بود (Bode) در بالا میبینیم که در دو نقطه فرکانس گوشه یا قطع، خروجی از ۰dB به ۳dB- کاهش مییابد و با نرخ ثابت به افت خود ادامه میدهد. این افت یا کاهش بهره معمولا به عنوان ناحیه افت آرام منحنی پاسخ فرکانس شناخته میشود. در تمام مدارهای پایه تقویت کننده و فیلتر مرتبه یک، این نرخ افت آرام ۲۰dB/decade (دسی بل بر دهه) معادل ۶dB/octave (دسی بل بر اکتاو) تعریف میشود. این مقادیر با توجه به مرتبه مدار چند برابر میشوند.
این نقاط فرکانس گوشه ۳dB- فرکانسی را تعریف میکنند که در آن بهره خروجی به %۷۰/۷۱ حداکثر مقدار خود کاهش مییابد. پس میتوان به درستی گفت که نقطه -3dB فرکانسی است که در آن بهره سیستم به ۰/۷۰۷ برابر حداکثر مقدار خود کاهش یافته است.
نقطه -3dB پاسخ فرکانسی
نقطه ۳dB- به عنوان نقطه نیمه توان نیز شناخته میشود، زیرا توان خروجی در این فرکانسهای گوشه نصف مقدار حداکثر خود در ۰dB خواهد بود.
در نقطه fL یا fH، ولتاژ (V) یا جریان (I) برابر با %۷۰/۷۱ حداکثر مقدار خود هستند. بنابراین، اگر R=۱Ω، آن گاه:

بنابراین، مقدار توان خروجی تحویل داده شده به بار در فرکانس قطع عملا «نصف» شده است و بدین ترتیب میتوان پهنای باند (BW) منحنی پاسخ فرکانس را به عنوان محدوده فرکانسهای بین این دو نقطه نیمه توان تعریف کرد.
در حالی که برای بهره ولتاژ از ۲۰log10(Av) و برای بهره جریان از ۲۰log10(Ai) استفاده میکنیم، برای بهره توان از ۱۰log10(Ap) استفاده میشود. توجه داشته باشید که ضریب ۲۰ به این معنی نیست که دو برابر ۱۰ باشد، چراکه دسی بل واحد نسبت توان است و معیاری از سطح توان واقعی نیست. همچنین بهره برحسب dB میتواند مثبت یا منفی باشد، به طوری که مقدار مثبت نشان دهنده تقویت و مقدار منفی نشان دهنده تضعیف است.
پس میتوانیم رابطه بین بهره ولتاژ، جریان و توان را در جدول زیر نمایش دهیم.
معادل های بهره بر حسب دسی بل
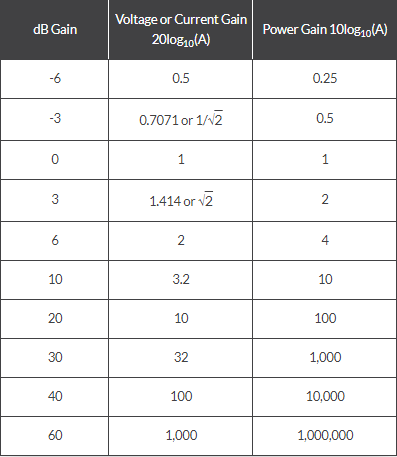
تقویت کنندههای عملیاتی میتوانند بهره ولتاژ حلقه باز (AVO) بیش از ۱۰۰۰۰۰۰ یا ۱۰۰dB داشته باشند.
دسی بل - مثال ۱
اگر یک سیستم الکترونیکی هنگام اعمال سیگنال ۱۲mV، ولتاژ خروجی ۲۴mV تولید کند، مقدار ولتاژ خروجی سیستم را بر حسب دسی بل محاسبه کنید.
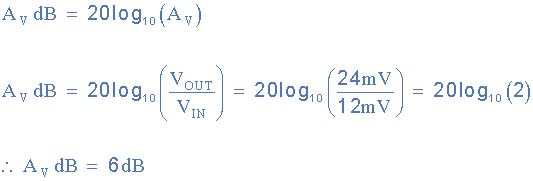
دسی بل - مثال ۲
اگر توان خروجی یک تقویت کننده صوتی در زمانی که فرکانس سیگنال ۱kHz است، ۱۰W و هنگامی که فرکانس سیگنال ۱۰kHz است، ۱W اندازه گیری شود، تغییر توان را بر حسب dB محاسبه کنید.
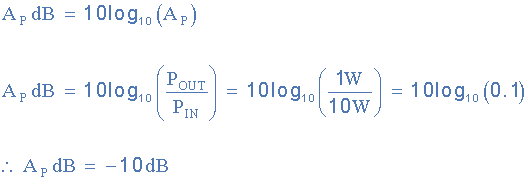
خلاصه پاسخ فرکانسی
در این آموزش دیدیم که چگونه دامنه فرکانسهایی که یک مدار الکترونیکی در آنها کار میکند با پاسخ فرکانسی آن مدار تعیین میشود. پاسخ فرکانسی یک دستگاه یا مدار، با نشان دادن چگونگی تغییر بهره آن یا میزان سیگنالی که از خود عبور میدهد، عملکرد آن را در محدوده مشخصی از فرکانسهای سیگنال توصیف میکند.
نمودارهای بود نمایش گرافیکی مشخصه پاسخ فرکانسی مدار هستند و میتوانند در حل مشکلات طراحی مورد استفاده قرار گیرند. به طور کلی، توابع بهره و فاز مدار در نمودارهای جداگانه با استفاده از مقیاس فرکانس لگاریتمی در امتداد محور x نشان داده میشوند.
پهنای باند محدوده فرکانسی است که یک مدار در بین نقاط فرکانس قطع بالا و پایین آن کار میکند. این نقاط فرکانس قطع یا گوشه، فرکانسهایی را نشان میدهند که در آنها توان مربوط به خروجی به نصف حداکثر مقدار خود کاهش مییابد. این نقاط نیمه توان مربوط به کاهش ۳dB (۰/۷۰۷۱) نسبت به حداکثر مقدار بهره است.
اکثر تقویت کنندهها و فیلترها دارای مشخصه پاسخ فرکانسی مسطح هستند که در آن پهنای باند یا باند گذر مدار مسطح و در طیف وسیعی از فرکانسها ثابت است. مدارهای تشدید کننده طوری طراحی شدهاند که محدودهای از فرکانسها را عبور داده و فرکانسهای دیگر را مسدود کنند. این فیلترها با استفاده از مقاومت، سلف و خازن ساخته میشوند که راکتانسشان با فرکانس متغیر است. منحنی پاسخ فرکانسی آنها ممکن است مانند یک افزایش شدید یا قله به نظر برسد، زیرا پهنای باند آنها تحت تاثیر رزونانس قرار میگیرد که به Q (ضریب کیفیت) مدار بستگی دارد، چراکه هرچه Q بیشتر باشد، پهنای باند باریکتر است.