فهرست مطالب
بهره ولتاژ حلقه باز، که معمولا بطور مخفف با AVOL (یا بطورساده AV) بیان میشود، برای اکثر آپ امپهای فیدبک ولتاژ تقریبا بالا است. مقادیر معمول 000, 100 تا 1,000,000 ، 10 یا 100 برابر این ارقام برای دستگاهها با دقت بالا هستند. برخی آپ امپهای سریع بهره حلقه باز بسیار کمتر دارند، اما بهرههای کمتر از چند هزار برای کاربرد بسیار دقیق نامطلوب هستند. همچنین توجه داشته باشید که بهره حلقه باز نسبت به دما پایدار نیست، و میتواند از دستگاهی به دستگاه دیگر از نوع مشابه بطور گسترده تغییر کند، بنابراین مهم است که به اندازه کافی بالا باشد.
به دلیل اینکه در یک آپ امپ فیدبک به صورت ورودی ولتاژ به خروجی ولتاژ عمل میکند، بهره حلقه باز آن یک نسبت بدون بُعد است، بنابراین هیچ واحدی لازم نیست. با اینحال، گاهی اوقات دیتاشیت به دلیل راحتی استفاده از اعداد کوچکتر بهره را بجای ولت بر ولت (V/V) برحسب ولت بر میلیولت (V/mV) یا (V/μV) بیان میکند. همچنین بهره ولتاژ میتواند برحسب دسیبل (dB) بیان شود، بطوریکه بهره برابر 20 بر حسب dB است، بنابراینبهره حلقه باز1V/μV برابر با 120dB است.
آپ امپهای فیدبک جریان یک ورودی جریان و یک خروجی ولتاژ دارند، از اینرو بهره امپدانس انتقالی آنها برحسب ولت بر آمپر یا اهم (kΩ یا MΩ) بیان میشود. مقادیر معمولا بین 100ها کیلواهم تا 10ها مگاهرتز هستند.
از نظریه فیدبک پایه، میتوان دریافت که برای حفظ دقت، بهره حلقه باز جریان مستقیم (dc) یک آپامپ دقیق (AVOL) باید بالا باشد. این امر میتواند از طریق بررسی معادله بهره حلقه بسته مشاهده شود، که خطاهای ناشی از بهره محدود را دربرمیگیرد. این عبارت برای بهره حلقه بسته با یک خطای بهره محدود بصورت زیر است:
[katex] G= \frac{1}{ \beta } ( \frac{1}{1+ \frac{1}{ A_{ V_{OL} }\times \beta }} ) [/katex] معادله ۱
که در آن حلقه فیدبک، یا شاخص فیدبک (تضعیف ولتاژ شبکه فیدبک) است.
به دلیل اینکه بهره نویز برابر با [katex] \frac{1}{ \beta} [/katex] است، شکلهای دیگری از این عبارت وجود دارد. با ترکیب دو جمله سمت راست و استفاده از عبارت بهره نویز (NG)، یک محاسبه دیگر برابر است با:
[katex] G_{CL} = \frac{NG}{ 1+\frac{NG}{ A_{ V_{OL} } } } [/katex] معادله ۲
معادله 1 و معادله 2 معادل هستند، و هردو میتوانند بکاربرده شوند. همانطورکه قبلا اشاره شد، بهره نویز بهرهای است که یک منبع ولتاژ کوچک سری با ورودی آپ امپ به سادگی تشخیص میدهد؛ این بهره سیگنال آپامپ ایدهآل در حالت غیرمعکوسکننده است. اگر AVOL در معادله 1 و معادله 2 بینهایت باشد، بهره حلقه بسته دقیقا برابر با بهره نویز، [katex] \frac{1}{ \beta} [/katex] میشود.
بههرحال، برای AVOL>> NG و AVOL بینهایت، یک تخمین خطای بهره حلقه به صورت زیر وجود دارد:
خطای حلقه بسته (٪) معادله ۳ ≈[katex] \frac{NG}{ A_{ V_{OL} } } \times 100 [/katex]
با توجه به معادله 3 درصد خطای بهره مستقیما متناسب با بهره نویز است؛ تاثیرات AVOL محدود برای بهره پایین کمتر هستند. برخی از مثالها نکات کلیدی در مورد این روابط بهره را نشان میدهند.
عدم قطعیت بهره حلقه باز
شرایط زیر را برای مثال الف و مثال ب بررسی کنید:
[katex] \frac{1}{ \beta }[/katex] =NG= بهره حلقه بسته ایده آل
بهره حلقه بسته واقعی = [katex] \frac{1}{ \beta } \mid \frac{1}{1+ \frac{ A_{ V_{OL} } }{ \beta } } \mid [/katex]
خطای حلقه بسته ≈ [katex] \frac{NG}{ A_{ V_{OL} } } \times 100[/katex] (NG<< AVOL)
برای مثال الف، بهره نویز 1000 نشان میدهد که برای بهره حلقه باز 2 میلیون، خطای بهره حلقه بسته در حدود %0.05 است. توجه داشته باشید که اگر بهره حلقه باز در سر تا سر دما و برای بارهای خروجی و ولتاژهای مختلف ثابت باقی بماند، خطای بهره %0.05 میتواند به بدون اندازهگیری به آسانی تنظیم شود، و هیچ خطای کلی بهره سامانه باقی نماند. اگر، با اینحال، بهره حلقه باز تغییر کند، بهره حلقه بسته حاصل نیز تغییر میکند، در نتیجه عدم قطعیت بهره مطرح میشود.
بنابراین، مثال الف 2,000,000=AVOL و 1000= NGدرنظرمیگیرد، درنتیجه منجر به خطای بهرهای در حدود %0.05 میشود.
برای مثال ب، فرض کنید AVOL به 300,000 کاهش مییابد؛ از اینروخطای بهره %0.33 میشود. این وضعیت یک عدم قطعیت %0.28 در بهره حلقه بسته به صورت زیر ایجاد میکند:
%0.28 =%0.05 -%0.33 = عدم قطعیت بهره حلقه بسته
در اکثر کاربردها، هنگام استفاده از یک آپ امپ خوب، مقاومتهای بهره مدار بزرگترین منبع خطای مطلق هستند. علاوه براین، عدم قطعیت بهره نمیتواند با تنظیم از بین برود.
تغییرات در سطح ولتاژ خروجی و بار خروجی معمولترین دلایل تغییرات در بهره حلقه باز آپ امپها هستند. یک تغییر در بهره حلقه باز با سطح سیگنال مجزا غیرخطی بودن را در تابع انتقال بهره حلقه بسته ایجاد میکند، که در حین تنظیم سامانه نیز نمیتواند حذف شود. اکثر آپ امپها بارهای ثابت دارند، بنابراین تغییرات AVOL با بار بطورکلی مهم نیستند. با اینحال، حساسیت AVOL به سطوح سیگنال خروجی ممکن است برای جریانهای بار بالاتر افزایش یابد.
شدت این غیرخطی بودن از یک نوع دستگاه به دیگری بسیار تغییر میکند، و بطورکلی در دیتاشیت مشخص نمیشود. حداقل AVOL همیشه مشخص میشود، و انتخاب یک آپ امپ با AVOL بالا احتمال خطاهای غیرخطی بودن بهره را حداقل میسازد. بسته به طراحی آپامپ غیرخطی بودن بهره میتواند از منابع بسیاری بدست آید. یک منبع متداول فیدبک حرارتی(برای مثال، از یک طبقه خروجی داغ به طبقه ورودی) است. اگر تغییر دما تنها دلیل خطای غیرخطی بودن باشد، میتوان پذیرفت که حداقلسازی بار خروجی مفید است. برای اثبات این موضوع، غیرخطی بودن در حالت بدون بار اندازهگیری میشود و سپس با حالت باردار مقایسه میشود.
اندازهگیری غیرخطی بودن بهره حلقه باز
صفحه نمایش X-Y اسیلوسکوپ برای یک مدار آزمایشی به منظور اندازهگیری غیرخطی بودن بهره حلقه باز dc در شکل1 نشان داده شده است. اقدامات احتیاطی مربوط به مدار آزمایشی ولتاژ آفست که قبلا بررسی شد باید در این مورد نیز رعایت شود.
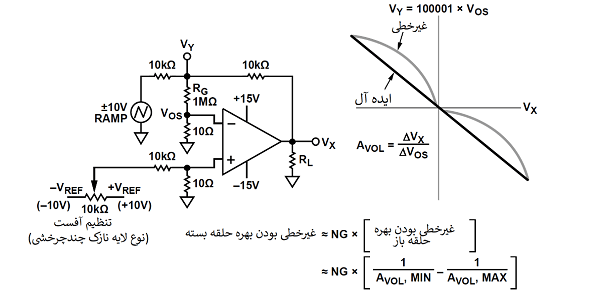
تقویتکننده برای یک بهره سیگنال 1- پیکربندی میشود. بهره حلقه باز به صورت تقسیم تغییر ولتاژ ورودی بر تغییر ولتاژ آفست ورودی تعریف میشود. با اینحال، برای مقادیر بزرگ ، آفست واقعی ممکن است فقط چند میکرو ولت در کل نوسان ولتاژ خروجی تغییر کند. بنابراین، مقسم مدار متشکل از مقاومت 10Ω و RG (1MΩ ) ولتاژ گره را به VY تغییر میدهد که به صورت زیر تعریف میشود:
[katex] V_{Y} = (1+ \frac{ R_{G} }{10Ω }) V_{os} =100,001 \times V_{os} [/katex] معادله ۴
مقدار RG بسته به مقدار Vos مورد انتظار به گونهای انتخاب میشود که ولتاژهای قابل اندازهگیری را در VY بدهد.
خروجی تولیدکننده شیب 10± ولت در بهره سیگنال، 1-، ضرب میشود و سبب میشود ولتاژ خروجی آپ امپ از 10+ تا 10– ولت تغییر کند. به دلیل ضریب بهره اعمالشده به ولتاژ آفست، پتانسیومتر برای تنظیم آفست افزوده میشود تا آفست خروجی اولیه صفر شود. مقادیر مقاومت انتخابشده ولتاژ آفست ورودی تا حدود 10 ± میلی ولت را صفر میکند. برای جلوگیری از رانش خروجی در هر انتهای پتانسیومتر از منابع ولتاژ ثابت، مثل AD688، استفاده کنید. توجه داشته باشید که فرکانس تولیدکننده شیب باید بسیار کم باشد، به دلیل فرکانس گوشه پایین بهره حلقه باز احتمالا بیشتر از کسری از 1 هرتز نیست (برای مثال، برای OP177 بسیار کم 0.1 هرتز است).
نمودار سمت راست شکل 1، VY رسم شده بر حسب Vxرا نشان میدهد. اگر بهره غیرخطی بودن نباشد، نمودار یک شیب ثابت دارد، و AVOL بصورت زیر محاسبه میشود:
[katex] A_{ V_{OL} } = \frac{ \Delta V_{x} }{ \Delta V_{Y} } =(1+ \frac{ R_{G} }{10Ω} )( \frac{ \Delta V_{x} }{ \Delta V_{Y} } )=100,000( \frac{ \Delta V_{x} }{ \Delta V_{Y} } ) [/katex] معادله ۵
اگر غیرخطی بودن وجود داشته باشد، وقتی سیگنال خروجی تغییر میکند بصورت پویا تغییر میکند.
غیرخطی بودن بهره حلقه باز تقریبی براساس مقادیر حداکثر و حداقل AVOL در گستره ولتاژ خروجی محاسبه میشود.
غیرخطی بودن بهره حلقه باز=[katex]\frac{1}{ A_{ V_{OL,min} } } -\frac{1}{ A_{ V_{OL,max} } } [/katex] معادله ۶
غیرخطی بودن بهره حلقه بسته با ضرب غیرخطی بودن بهره حلقه باز در NG بدست میآید.
غیرخطی بودن بهره حلقه بسته=NG×[katex]\frac{1}{ A_{ V_{OL,min} } } -\frac{1}{ A_{ V_{OL,max} } } [/katex] معادله ۷
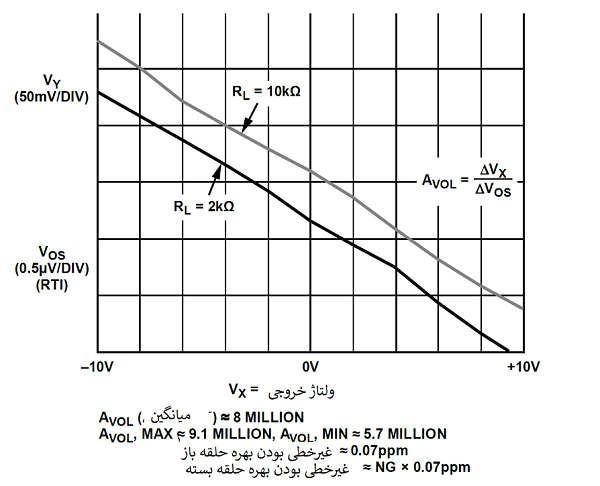
در یک حالت ایدهآل، نمودار Vos برحسب Vx شیب ثابتی دارد، و بهره حلقه باز AVOL، معکوس این شیب است. یک خط افقی با شیب صفر بهره حلقه باز بینهایت را نشان میدهد. در یک آپامپ واقعی، شیب ممکن است به دلیل غیرخطی بودن، فیدبک حرارتی، و دیگر شاخصها در سراسر گستره خروجی تغییر کند. شیب حتی ممکن تغییر علامت دهد.
شکل 2 نمودار VY (و Vos) را برحسب Vx برای یک آپ امپ دقیق OP177 نشان میدهد. این نمودار برای دو بار مختلف، 2 کیلواهم و 10 کیلواهم نشان داده میشود. معکوس شیب براساس نقاط انتهایی محاسبه میشود، و AVOL میانگین در حدود 8 میلیون است. مقادیر حداکثر و حداقل AVOL در سراسر گستره ولتاژ خروجی تقریبا به ترتیب 9.1 میلیون، و 5.7 میلیون اندازهگیری می شوند. این مشابه یک غیرخطی بودن بهره حلقه بسته در حدود 0.07ppm است.
البته، این اندازهگیریهای غیرخطی، بیشترین کاربرد را در مدارهای dc با دقت بالا دارند. همچنین برای کاربردهای با پهنای باند وسیعتر، همانند یک سیگنال صوتی مناسب هستند. روش نمایش X-Y نشان داده شده در شکل 1 اعوجاج متقاطع را، برای مثال در طبقه خروجی آپ امپ با طراحی ضعیف به سادگی نشان میدهد.