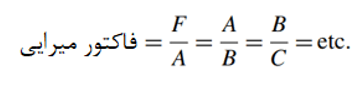مشخصه دینامیک سنسور
در شرایط استاتیک، یک سنسور بهطورکامل با تابع انتقال، بازه، کالیبراسیون و غیره، توصیف میشود. با اینحال، هنگامیکه محرک ورودی متفاوت است؛ پاسخ سنسور معمولا با وفاداری کامل دنبال نمیشود. دلیل آن این است که هم حسگر و همجفتشدن آن با منبع محرک، همیشه نمیتوانند فورا پاسخ دهند.
بهعبارتدیگر سنسور ممکن است با یک مشخصهی وابسته به زمان مشخص شود که به آن مشخصهی دینامیک میگویند.
اگر یک سنسور فورا پاسخ ندهد؛ ممکن است مقادیر محرکهایی را نشان دهد که تا حدودی متفاوت از واقعیت هستند؛ یعنی سنسور با خطای دینامیکی، پاسخ میدهد. اختلاف بین خطاهای استاتیک و دینامیک این است؛ که دومی همیشه وابسته به زمان است. اگر یک سنسور بخشی از یک سیستم کنترلی باشد که ویژگیهای دینامیکی خاص خود را دارد، این ترکیب میتواند در بهترین حالت، باعث تاخیر در نمایش مقدار واقعی یک محرک و یا در بدترین حالت، باعث نوسان شود.
زمان گرمکردن، زمانی بین اعمال توان الکتریکی به سنسور یا سیگنال تحریک و لحظهای است که سنسور میتواند با دقت مشخصشدهی خود، کار کند. بسیاری از سنسورها، زمان گرمشدن بسیار کوتاهی دارند. با اینحال، برخی از آشکارسازها، بهویژه آنهایی که در یک محیط کنترلشدهی حرارتی (ترموستات) کار میکنند؛ ممکن است به ثانیهها و دقیقهها زمان گرمشدن نیاز داشتهباشند تا در محدودههای دقت مشخصشدهشان ،کاملا عملیاتی شوند.
در تئوری سیستم کنترل، رابطهی ورودی-خروجی معمولا از طریق یک معادلهی دیفرانسیل خطی با ضریب ثابت توصیف میشود. سپس با ارزیابی چنین معادلهای میتوان مشخصههای دینامیکی (وابسته به زمان) سنسور را مطالعه کرد. بسته به طراحی سنسور، معادلهی دیفرانسیل میتواند چندین مرتبه داشته باشد. یک حسگر مرتبهی صفر، با رابطهای مشخص میشود؛ که برای یک تابع انتقال خطی، یک معادلهی اصطلاحشدهی معادله : S = a+bs است؛ درجاییکه، ورودی و خروجی آن، تابعی از زمان t میباشند:
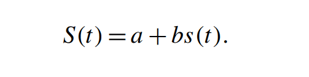
مقدار a را آفست و b را حساسیت استاتیک، مینامند.
معادلهی بالا مستلزم آن است که سنسور هیچ المان ذخیرهی انرژی مانند خازن یا جرم را در خود جای ندهد. یک سنسور درجه صفر، فورا پاسخ میدهد. بهعبارت دیگر، چنین سنسوری، بههیچ ویژگی دینامیکی، نیاز ندارد.
یک معادله دیفرانسیل مرتبه اول، سنسوری را توصیف میکند؛ که یک المان ذخیرهی انرژی را در خود جای دادهاست. رابطهی بین ورودی s(t) و خروجی S(t) معادلهی دیفرانسیل زیر است:
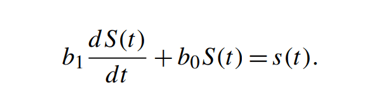
یک مثال معمولی از یک سنسور مرتبهی اول، یک سنسور دما است؛ که ذخیرهی انرژی برای آن، ظرفیت حرارتی است. سنسورهای مرتبهی اول، ممکن است توسط سازنده به روشهای مختلفی مشخص شوند. یک پاسخ فرکانسی معمول است؛ که مشخص میکند یک سنسور مرتبه اول، با چه سرعتی میتواند به تغییر در محرک ورودی، واکنش نشان دهد.
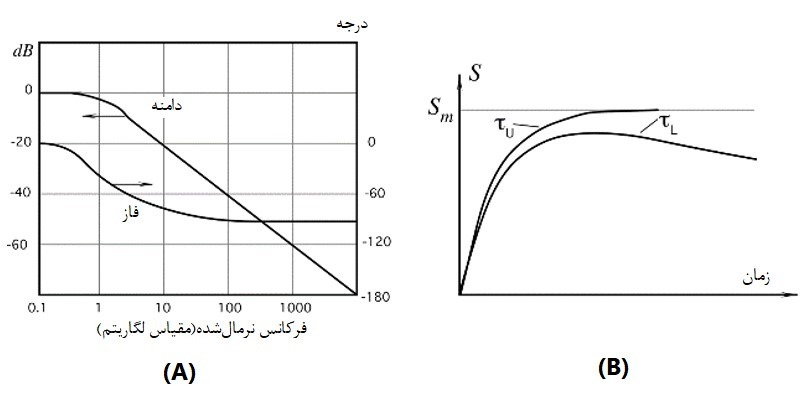
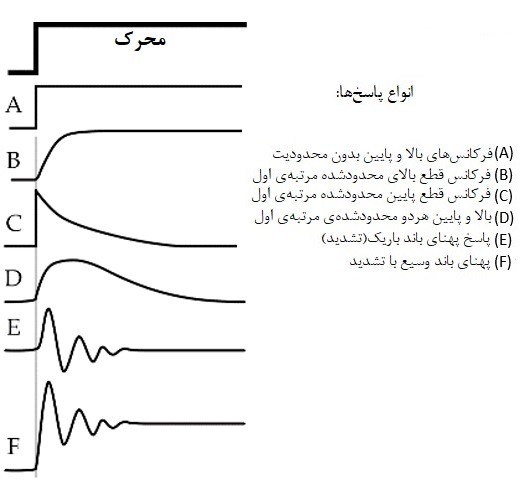
پاسخ فرکانسی برحسب هرتز یا رادیان بر ثانیه است؛ تا کاهش نسبی سیگنال خروجی را در یک فرکانس مشخص، تعیین کند ( نمودار شکل بالا – A). یک عدد کاهشی رایج (محدودیت فرکانس) 3- دسیبل است، که نشان میدهد در چه فرکانسی، ولتاژ (یا جریان) خروجی، حدود 30% کاهش مییابد. حد پاسخ فرکانسی fu اغلب فرکانس قطع بالا نامیده میشود؛ زیرا بالاترین فرکانسی است که سنسور در آن میتواند پردازش کند.
پاسخ فرکانسی، مستقیما به یک پاسخ سرعت مربوط میشود که در واحدهای محرک ورودی در واحد زمان، تعریف میشود. تعیین پاسخ فرکانس یا سرعت در هر مورد خاص، به نوع سنسور، کاربرد آن و اولویتهای طراح بستگی دارد.
راه دیگر، برای تعیین پاسخ سرعت براساس زمان است که سنسور باید با قرارگرفتن در معرض یک محرک پله، به 90 درصد از حالت پایدار یا حداکثر سطح در مواجهه با یک محرک گام برسد. برای پاسخ مرتبه اول، استفاده از ثابت زمانی، بسیار راحت است. ثابت زمانی،T اندازهگیری اینرسی سنسور است. از نظر الکتریکی، برابر است با حاصلضرب ظرفیت و مقاومت الکتریکی: T=CR. در اصطلاح حرارتی، بهجای آن، باید از ظرفیت حرارتی و مقاومتهای حرارتی، استفاده کرد. عملا ثابت زمانی را میتوان بهراحتی اندازهگیری کرد. پاسخ سیستم مرتبه اول بهصورت زیر است:
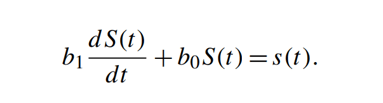
در این معادله، Sm خروجی حالت پایدار، t زمان و e پایهی لگاریتم طبیعی است. با جایگزینی t=T :
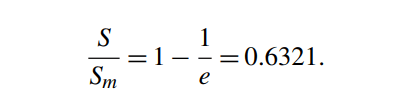
به عبارت دیگر، پس از گذشت زمان برابر با یک ثابت زمانی، پاسخ به حدود 63 درصد از سطح حالت پایدار خود میرسد. به همین ترتیب، میتوان نشان داد که پس از دو ثابت زمانی، ارتفاع به 86.5% و پس از سه ثابت زمانی 95% خواهد بود.
فرکانس قطع، نشاندهندهی کمترین یا بیشترین فرکانس محرکی است که سنسور میتواند پردازش کند. فرکانس قطع بالا، نشان میدهد که سنسور با چه سرعتی، واکنش میدهد. فرکانس پایینتر نشان میدهد که سنسور تا چه حد کند، میتواند محرکهای درحال تغییر را پردازش کند. نمودار شکل بالا-B پاسخ سنسور را هنگامیکه، فرکانسهای قطع بالا و پایین محدود هستند؛ نشان میدهد. بهعنوان یک قاعدهی کلی میتوان از یک فرمول ساده برای ایجاد ارتباط بین فرکانس قطع، fc (بالا و پایین) و ثابت زمانی در یک سنسور مرتبه اول، استفاده کرد:
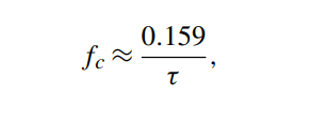
تغییر فاز در یک فرکانس خاص، مشخص میکند؛ که چگونه سیگنال خروجی در نمایش تغییر محرک، عقب میماند( شکل A). شیفت زاویهای برحسب درجه یا رادیان، اندازهگیری میشود و معمولا برای سنسوری که سیگنالهای پریودیک را پردازش میکند؛ مشخص میشود.
اگر یک حسگر، بخشی از یک سیستم کنترل فیدبک باشد؛ دانستن مشخصهی فاز آن، بسیار مهم است. تاخیر فاز، حاشیهی فاز سیستم را کاهش میدهد و میتواند منجر به ناپایداری کلی شود. یک معادلهی دیفرانسیل مرتبه دوم، سنسوری را توصیف میکند؛ که دو المان ذخیرهی انرژی را در خود جای دادهاست. رابطهی بین ورودی s(t) و خروجی S(t) معادلهی دیفرانسیل زیر است:
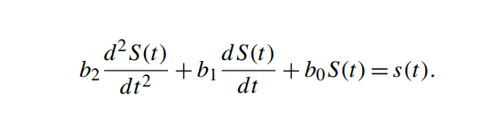
نمونهای از سنسورهای مرتبه دوم، شتابسنجهایی هستند که جرم و فنر را در خود جای دادهاند. یک پاسخ مرتبه دوم، برای حسگری که با یک سیگنال پریودیک، پاسخ میدهد؛ خاص است. چنین پاسخ دورهای، میتواند بسیار مختصر باشد و میتوان گفت که سنسور میرایی دارد؛ یا ممکن است زمان طولانی داشتهباشد و حتی ممکن است؛ بهطور مداوم در نوسان باشد. بهطور طبیعی برای یک سنسور، چنین نوسان مداوم یک نقص است و باید از آن اجتناب شود.
هر حسگر مرتبه دوم، ممکن است؛ با فرکانش تشدید(طبیعی) مشخص شود؛ که عددی است که برحسب هرتز یا رادیان برثانیه بیان میشود. فرکانس طبیعی، نشان میدهد سیگنال خروجی سنسور، بهمیزان قابل توجهی، افزایش مییابد. بسیاری از سنسورها، طوری رفتار میکنند؛ که گویی خروجی سنسور پویا با منحنی استاندارد یک پاسخ مرتبه دوم، مطابقت دارد. فرکانس تشدید، میتواند به خواص مکانیکی، حرارتی یا الکتریکی آشکارساز، مربوط باشد.
بهطورکلی، محدودهی فرکانس کاری سنسور باید بسیار پایینتر ( حداقل 60%) یا بالاتر از فرکانس تشدید، انتخاب شود. با این حال، در برخی از سنسورها، فرکانس تشدید نقطهی عملکرد است. بهعنوان مثال، در آشکارسازهای شکست شیشه ( که در سیستمهای امنیتی، استفاده میشود) رزونانس سنسور را بهطور انتخابی نسبت به پهنای باند باریک، حساس میکنند؛ که مخصوص طیف صوتی تولیدشده توسط شیشههای خرد شدهاست.
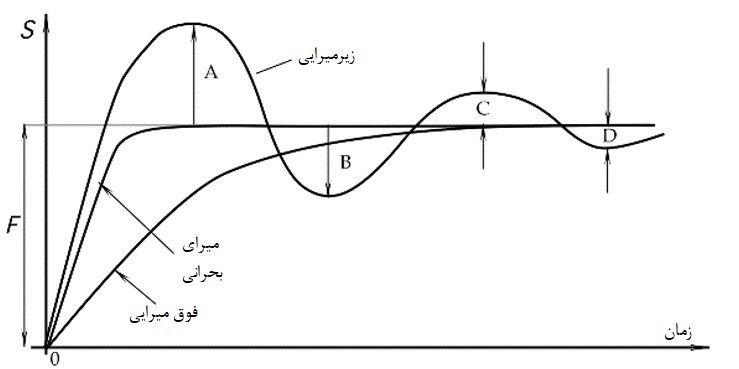
میرایی یا دمپینگ (Damping) کاهش یافتن یا سرکوب پیشروندهی نوسان در سنسور با پاسخهایی بالاتر از پاسخ مرتبه اول است. هنگامیکه، پاسخ سنسور تا حد امکان سریع و بدون افزایش بیش از حد باشد؛ گفته میشود، که پاسخ به میرایی بحرانی، تبدیل شدهاست (شکل 2). پاسخ زیرمیرایی (underdamping)، زمانی اتفاق میافتد؛ که اورشوت (overshoot)(جهش زیاد) اتفاق افتد و پاسخ فوق میرا (overdamping)، کندتر از پاسخ میرای بحرانی است. نسبت میرایی عددی است؛ که ضریب میرایی واقعی مبدل خطی مرتبه دوم را با میرایی بحرانی، بیان میکند.
برای یک پاسخ نوسانی، همانطور که در شکل 2 نشان داده شدهاست؛ یک ضریب میرایی، معیاری از میرایی است؛ که( بدون علامت) بهعنوان ضریب بزرگتر با کوچکتر از یک جفت، نوسان متوالی در جهت مخالف سیگنال خروجی، درحدود یک مقدار در نهایت حالت پایدار، بیان میشود. بنابراین، ضریب میرایی را میتوان بهصورت زیر اندازهگیری کرد: