تابع انتقال سنسور

بازدید: 1159

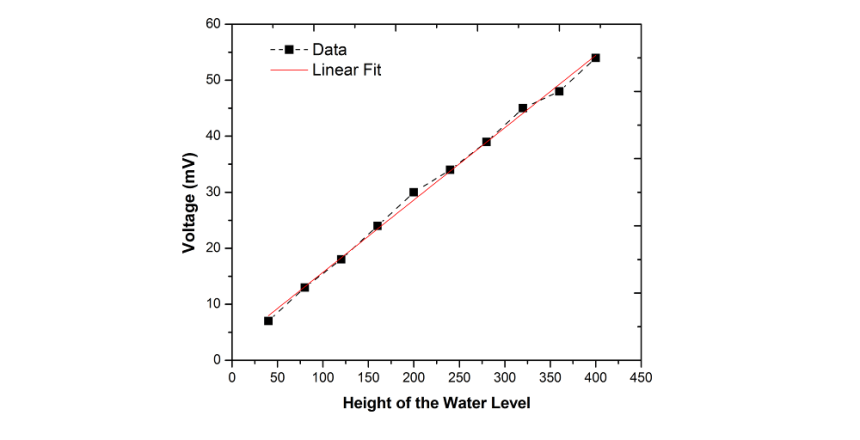
برای هر سنسور یک رابطه‌ی ایده‌آل یا تئوری بین خروجی و محرک وجود دارد. اگر سنسور با متریال ایده‌آل، توسط کارگران ایده‌آل و با استفاده از ابزارهای ایده‌آل طراحی و ساخته شود؛ خروجی چنین سنسوری همیشه ارزش واقعی محرک را نشان می‌دهد.

این تابع ایده‌آل، ممکن است به شکل جدول مقادیر، نمودار یا معادله‌ی ریاضی بیان شود. یک رابطه‌ی خروجی- محرک ایده‌آل (نظری) با به اصطلاح تابع انتقال (Transfer Function)، مشخص می‌شود. این تابع، رابطه بین سیگنال الکتریکی S تولیدشده توسط سنسور و محرک s را تعیین می‌کند (S=f(s)). این تابع، ممکن است بصورت یک رابطه خطی ساده یا یک وابستگی غیرخطی باشد (به‌عنوان مثال، تابع لگاریتمی، نمایی یا توان). در بسیاری از موارد، رابطه یک بعدی است (یعنی خروجی در مقابل یک محرک در ورودی). یک رابطه‌ی خطی تک بعدی، با معادله‌ی زیر نشان داده می‌شود:

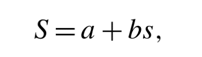
که در آن a، نقطه‌ی قطع (یعنی سیگنال خروجی در سیگنال ورودی صفر) و b، شیب نمودار است که گاهی اوقات، حساسیت (sensitivity) نامیده می‌شود. S یکی از مشخصه‌های سیگنال الکتریکی خروجی است که توسط المان‌های جمع‌آوری داده (data acquisition) به‌عنوان خروجی سنسور استفاده می‌شود و بسته به خواص سنسور، ممکن است دامنه، فرکانس یا فاز باشد.

تابع انتقال لگاریتمی سنسور

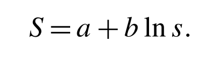
تابع انتقال نمایی سنسور

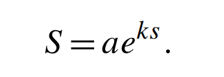
تابع انتقال توانی سنسور

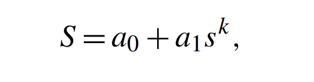
در این معادله، k عدد ثابت است.

یک سنسور ممکن است تابع انتقالی داشته باشد که هیچ یک از تقریب‌های بالا، به‌اندازه‌ی کافی برای آن مناسب نباشند. در این صورت، یک تقریب چندجمله‌ای مرتبه بالاتر برای آن استفاده می‌شود.

برای یک تابع انتقال غیرخطی، ضریب حساسیت b؛ مانند رابطه‌ی خطی (معادله‌ی 1) یک عدد ثابت نیست. به ازای هر مقدار ورودی خاص s₀ می‌توان آن را به‌صورت زیر تعریف کرد:

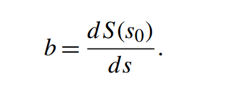
در بسیاری از موارد، یک سنسور غیرخطی ممکن است در یک بازه‌ی محدود، خطی درنظر گرفته‌شود. در بازه های گسترده ،یک تابع انتقال غیرخطی، ممکن است توسط چندین خط مستقیم مدل شود. که به‌این تقریب، تقریب تکه‌ای (piecewise approximation) گفته می‌شود. برای تعیین اینکه آیا یک تابع را می‌توان با یک مدل خطی نشان داد؛ متغیرهای افزایشی برای ورودی در حین مشاهده‌ی خروجی، معرفی می‌شوند. اختلاف بین پاسخ واقعی و مدل خطی، با محدودیت‌های صحت مشخص‌شده، مقایسه می‌شود.

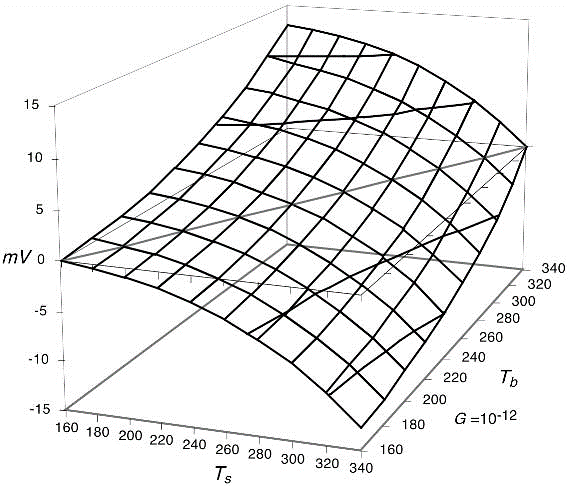
یک تابع انتقال می‌تواند زمانی‌که خروجی سنسور تحت تاثیر بیش از یک محرک ورودی قرار می‌گیرد؛ بیش از یک بُعد داشته باشد. مثال آن تابع انتقال یک سنسور تابش حرارتی (مادون قرمز) است. این تابع (این تابع، عموما با نام قانون استفان بولتزمن (Stefan–Boltzmann law)، شناخته می‌شود)، دو دما (Tb، دمای مطلق جسم اندازه‌گیری و Ts، دمای مطلق سطح سنسور) و ولتاژ خروجی V را به‌هم متصل می‌کند:

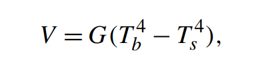
در معادله‌ی بالا، G یک عدد ثابت است. واضح است که رابطه‌ی بین دمای جسم و ولتاژ خروجی (تابع انتقال) نه تنها غیرخطی،(پارابولای مرتبه‌ی چهارم) است؛ بلکه به دمای سطح سنسور نیز بستگی دارد. برای تعیین حساسیت سنسور نسبت به دمای جسم، یک مشتق جزئی به‌صورت زیر گرفته می‌شود:

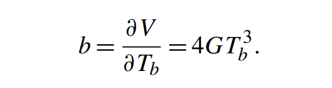
نمایش گرافیکی یک تابع انتقال دو بعدی معادله‌ی 6 در شکل زیر نشان داده شده‌است. مشاهده می‌شود که هر مقدار ولتاژ خروجی می‌تواند منحصربفرد باشد؛ که از دو دمای ورودی تعیین می‌شود.

لازم به ذکر است که یک تابع انتقال، نشان‌دهنده‌ی رابطه‌ی ورودی به خروجی است. با این‌حال هنگامی‌که یک حسگر برای اندازه‌گیری یا تشخیص یک محرک، استفاده می‌شود؛ یک تابع معکوس (خروجی به ورودی) باید به‌کار گرفته‌شود. وقتی، یک تابع انتقال، خطی باشد؛ محاسبه‌ی تابع معکوس، بسیار آسان است. هنگامی‌که غیرخطی است؛ کار پیچیده‌تر می‌شود و در بسیاری از موارد راه‌حل تحلیلی برای پردازش داده‌های نسبتا ساده مناسب نیست و در این موارد اغلب تقریب بهترین راه‌حل است.